Mô Hình Z-Score Và Điểm Số Tín Dụng Tiêu Dùng:

hàng này với thực tế trả nợ của họ xem 18 tỷ lệ đúng là bao nhiêu, đó chính là độ chính xác của kết quả dự báo.

 Mô hình Logit và Probit vè cơ bản thì giống nhau, chỉ có sự khác biệt về phân phối. Mô hình Logit thì tuân theo phân phối Logistic chuẩn tích lũy(F) còn mô hình Probit thì tuân theo phân phối chuẩn tích lũy (). Trong bài viết này tôi sẽ hướng dẫn chạy mô hình Logit bằng Eviews 8.0, và giải thích ý nghĩa của từng tham số trong mô hình. Mô hình Probit sẽ được đề cập đến trong các bài viết tiếp theo.

2.4.3. Mô hình Probit:

2.4.3.1. Giới thiệu mô hình Probit:

Mô hình Probit hay còn có tên gọi là mô hình normit. Tên gọi Probit bắt nguồn từ chữ Probability và unit. Mô hình này áp dụng đối với các biến phụ thuộc có dạng nhị phân. Ví dụ biến phụ thuộc là khả năng kết hôn của một người. Nếu người này kết hôn thì sẽ nhận giá trị 1 và ngược lại là 0.

Ý tưởng của mô hình Probit: Mô hình probit cho rằng quyết định kết hôn bị tác động bởi một biến tiềm ẩn nào đó. Biến tiềm ẩn này được gọi là chỉ số hữu dụng utility index I. Biến chỉ số này bị ảnh hưởng bởi các biến giải thích:

Ii 1 2 Xi

Có thể bạn quan tâm!

Xem toàn bộ 96 trang tài liệu này.

Một người sẽ quyết định kết hôn khi giá trị I này vượt qua một ngưỡng nào đó tạm gọi là I*. Giá trị I* này chúng ta không thể biết được nhưng giả định nó có phân phối chuẩn. Xác suất để người đó không kết hôn sẽ có dạng:

i i i i

P P I * I

P(Z



X ) F(

X )

1 2

Hàm F là hàm phân phối tích lũy chuẩn (CDF). Vì P là xác suất người đó kết hôn nên bạn phải tính nghịch đảo của F, do đó ta có công thức:

I F 1 (P ) X

i i 1 2 i

 Ước lượng biến tiềm ẩn

o Đối với dữ liệu theo nhóm

Từ thông tin từ mẫu, bạn có thể xác định được

Pi . Ví dụ khảo sát 100 người và

có 40 người kết hôn thì Pi  0.4 . Ii được ước lượng thông qua hàm CDF.

o Đối với dữ liệu cá biệt

Tương tự như mô hình xác suất tuyến tính, bạn vẫn phải sử dụng phương pháp ước lượng xác suất cực đại.

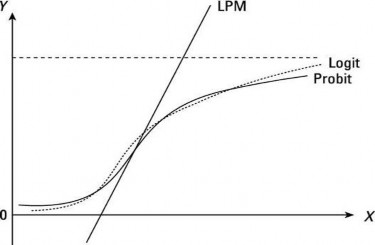
(Nguồn: amorfati.xyz)

Hình 2. 3. Đồ thị mô hình Probit

 Ý tưởng phân tích Probit được xuất bản trong khoa học bởi Chester Bliss trong năm 1934. Năm 1952, một Giáo sư về thống kê tại Đại học Endiburgh là David Finney đã viết lại một cuốn sách với tên gọi là “Phân tích Probit”.

 Cấu trúc dữ liệu trong mô hình Probit cũng tương tự như mô hình Logit, mô hình ước lượng xác suất trả nợ của một khách hàng. Mô hình Probit có giả thiết sai số ngẫu nhiên có sai số chuẩn hóa: N(01).

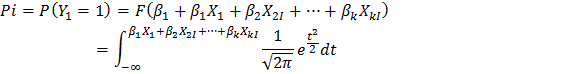
Trong đó F là hàm phân phối xác suất tích lũy. Khi đó hàm hợp lệ có dạng:

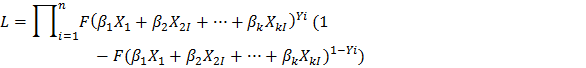
Các biến và tham số trong mô hình Probit tương tự như mô hình Logit.

2.4.3.2. Đặc điểm của mô hình Probit:

Ưu điểm: Xác suất (P) đại diện cho sự kết hợp tuyến tính của các nhân tố đưa vào mô hình xếp hàng. Với phương pháp ước lượng khác nhau, tuy nhiên kết quả của hai mô hình Logit và Probit khác nhau không đáng kể. Vì dễ dùng hơn trong trình bày toán học, các mô hình Logit và Probit thường được sử dụng cho mô hình XHTD trong thực tế, có khả năng lượng hóa được xác suất khả năng trả nợ hoặc trả nợ của KHDN.

Trong quá trình sử dụng mô hình này không đòi hỏi các gải thuyết về những nhân tố liên quan tới khả năng trả nợ, dữ liệu dù là định tính hay lượng tính thì đều có thể được xử lí mà không gặp phải bất cứ một vấn đề nào.

Nhược điểm:

Trong quá trình xử lí dữ liệu, đòi hỏi phải có một lượng dữ liệu đủ lớn cho mỗi phạm trù trong số liệu thống kê.

Ước lượng biến tiềm ẩn:

 Đối với dữ liệu theo nhóm: Từ thông tin từ mẫu, bạn có thể xác định

được Pi . Ví dụ khảo sát 100 người và có 40 người kết hôn thì .

Ii được ước lượng thông qua hàm CDF.

 Đối với dữ liệu cá biệt: Tương tự như mô hình xác suất tuyến tính, bạn vẫn phải sử dụng phương pháp ước lượng xác suất cực đại.

2.5. Mô hình Z-Score và điểm số tín dụng tiêu dùng:

2.5.1. Giới thiệu về mô hình:

 Công trình của Altman được xây dựng dựa trên nghiên cứu của nhà nghiên cứu kế toán William Beaver và những người khác. Trong những năm 1930 trở đi, Mervyn và những người khác đã thu thập các mẫu phù hợp và đánh giá rằng các tỷ lệ kế toán khác nhau dường như có giá trị trong việc dự đoán phá sản. Điểm Z của Altman là phiên bản tùy biến của ký thuật phân tích phân biệt đối xử của RA Fisher (1936).

 Công trình của William Beaver, được xuất bản vào năm 1966 và 1968, là người đầu tiên áp dụng phương pháp thống kê, kiểm tra để dự đoán phá sản cho một mẫu các công ty phù hợp. Beaver đã áp dụng phương pháp này để đánh giá tầm quan trọng của từng tỷ lệ kế toán dựa trên phân tích đơn biến, sử dụng từng tỷ lệ kế toán một lần. Cải tiến chính của Altman là áp dụng một phương pháp thống kê, phân tích phân biệt, có thể tính đến nhiều biến số cùng một lúc.

 Có nhiều công cụ đã được phát triển để làm việc này, trong đó chỉ số Z của Altman là công cụ được cả hai giới học thuật và thực hành công nhận và sử dụng rộng rãi trên thế giới. Chỉ số Altman Z-Score (gọi tắt là chỉ số Z-Score) được phát triển năm 1968 bởi giáo sư Edward I. Altman, trường kinh doanh Leonard N. Stern, thuộc trường Đại học New York, dựa vào việc nghiên cứu khá công phu trên số lượng nhiều công ty khác nhau tại Mỹ. Mặc dù chỉ số Z- Score này được tìm ra tại Mỹ, những hầu hết các nước, vẫn có thể sử dụng với độ tin cậy cao.

2.5.2. Cơ sở toán học và các khái niệm liên quan:

 Ban đầu giáo sư Altman sử dụng đến 22 chỉ tiêu tài chính (Financial Ratio) khác nhau để tính chỉ số Z-Score, sau đó ông phát triển thêm và rút gọn lại còn

sử dụng 5 chỉ tiêu. Cụ thể, Z-Score được tính với 5 chỉ số tài chính được ký hiệu từ X1, X2, X3, X4, X5 bao gồm:

 X1: Tỷ số vốn lưu động trên tổng tài sản (Working Capitals/Total Assets).

 X2: Tỷ số lợi nhuận giữ lại trên tổng tài sản (Retain Earning/Total Assets).

 X3: Tỷ số lợi nhuận trước lãi vay và thuế trên tổng tài sản (EBIT/Total Assets).

 X4: Giá trị thị trường của vốn chủ sở hữu trên giá trị số sách của tổng nợ (Market Value of Total Equity / Book values of total Liabilities).

 X5: Tỷ số doanh số trên tổng tài sản (Sales/Total Assets).

Ngoài ra, từ một chỉ số Z ban đầu, Giáo sư Edward I. Altman đã phát triển ra Z’ và Z’’ để có thể áp dụng theo từng loại hình và ngành của doanh nghiệp:

Đối với doanh nghiệp đã cổ phần hóa, ngành sản suất, Z-Score được tính theo công thức:

Z=1.2X1 + 1.4X2 + 3.3X3 + 0.64X4 + 0.999X5 (1)

 Nếu Z > 2.99: Doanh nghiệp nằm trong vùng an toàn, chưa có nguy cơ phá sản.

 Nếu 1.8 < Z < 2.99: Doanh nghiệp nằm trong vùng cảnh báo, có thể có nguy cơ phá sản.

 Nếu Z < 1.8: Doanh nghiệp nằm trong vùng nguy hiểm, nguy cơ phá sản cao.

Mô hình Z-Score áp dụng cho các công ty tư nhân:

Kết quả của mô hình Z-Score điều chỉnh với biến mới X4 là:

Đối với doanh nghiệp chưa cổ phần hóa, ngành sản suất Z-Score, kết quả của mô hình này điều chỉnh với biến mới X4 được tính theo công thức:

Z’=0.717X1 + 0.847X2 + 3.107X3 + 0.42X4 + 0.998X5 (2)

Các điểm ngưỡng cho chỉ số Z’ này như sau:

 Nếu Z’ > 2.9: Doanh nghiệp nằm trong vùng an toàn, chưa có nguy cơ phá sản.

 Nếu 1.23 > 2.9: Doanh nghiệp nằm trong vùng cảnh báo, có thể có nguy cơ phá sản.

 Nếu Z’ < 1.23: Doanh nghiệp nằm trong vùng nguy hiểm, nguy cơ phá sản cao.

Mô hình Z-Score điều chỉnh áp dụng cho các doanh nghiệp không sản suất

Đối với các doanh nghiệp khác: Chỉ số Z’’ dưới đây có thể được dùng cho hầu hết các ngành, các loại hình doanh nghiệp. Vì sự khác nhau khá lớn của X5 giữa các ngành, nên X5 đã được loại ra. Công thức tính chỉ số Z’’ được điều chỉnh như sau:

Z’’=6.56X1 + 3.26X2 + 6.72X3 + 1.05X4 (3)

 Nếu Z’’ > 2.6: Doanh nghiệp nằm trong vùng an toàn, chưa có nguy cơ phá sản.

 Nếu 1.2 < Z’’ < 2.6: Doanh nghiệp nằm trong vùng cảnh báo, có thể có nguy cơ phá sản.

 Nếu Z’’ < 1.1: Doanh nghiệp nằm trong vùng nguy hiểm, nguy cơ phá sản cao.

2.5.3. Đặc điểm của mô hình Z-Score:

 Trên thế giới chỉ số Altman’s Z-Score đã được áp dụng trong nhiều năm và nhiều quốc gia khác nhau như năm 1968 cho các doanh nghiệp nhỏ tại Mỹ, sau đó giáo sư Altman còn áp dụng Z-Score trong nghiên cứu của mình năm 1983, 1998 và 2000.

 Kết quả cho thấy chỉ số Z-Score đã dự báo chính xác tới khoảng 95% doanh nghiệp bị phá sản trong năm kết tiếp và 72% doanh nghiệp bị phá nghiệp sẽ

giúp cho NHTM có được dự báo sớm về rủi ro phá sản của doanh nghiệp, cũng chính là rủi ro tín dụng, nợ xấu tín dụng của NHTM.

 Do đó Z-Score là công cụ bổ trợ hữu ích cho NHTM trong xác định và dự báo và theo dòi rủi ro tín dụng của doanh nghiệp trong hoạt động tín dụng của mình.

Trên cơ sở những ưu điểm và khả năng áp dụng rộng rãi của Z-Score trong dự báo nợ xấu tín dụng của doanh nghiệp, NHTM nên xem xét thực thi một số giải pháp sau để tận dụng ưu điểm của Z-Score trong quản lý nợ xấu tín dụng của mình:

Một là, nên bổ sung chỉ số Z-Score vào các chỉ tiêu xếp hạng tín dụng nội bộ khi đánh giá tín dụng và ra quyết định cấp tín dụng cho khách hàng. Điều này giúp dự báo sớm khả năng phá sản cũng chính là rủi ro tín dụng của khách hàng. Chỉ cấp tín dụng cho những doanh nghiệp có mức Z-Score an toàn. Kiên quyết từ chối các doanh nghiệp có mức Z-Score thấp hoặc hạn chế cấp tín dụng cho các doanh nghiệp có Z-Score ở mức rủi ro.

Hai là, thường xuyên theo dòi, tính toán lại chỉ số Z-Score theo quy hoặc theo tháng để đánh giá rủi ro tín dụng của khách hàng và theo dòi chiều hướng thay đổi của Z-Score để phát hiện kịp thời rủi ro biện pháp can thiệp thích hợp.

Ba là, nên nghiên cứu sự thích hợp của Z-Score trong áp dụng cho từng nhóm đối tượng khách hàng để điều chỉnh các chỉ tiêu sao cho thích hợp tại Lào.

KẾT LUẬN CHƯƠNG 2

Chương này đã tập trung nghiên cứu và đưa ra một số phương pháp, mô hình cảnh báo nợ xấu tín dụng ngân hàng chẳng hạn như các mô hình CAEL, các mô hình chất lượng 6C, mô hình định tính – Mô hình 6C, mô hình xếp hạng các ngân hàng của Moody’s, Mô hình Standard & Poor’s (S&P); Một số mô hình hồi quy Logit-Probit trong cảnh báo nợ xấu tín dụng, mô hình Z-Score.

Bên cạnh đó, chương này còn chỉ ra những ưu nhược điểm của một số mô hình và đưa ra lựa chọn mô hình cho thử nghiệm ứng dụng.