n f
(0)
f (x(0) h ,..., x(0) h ) f (x(0) ,..., x(0) ) 1
n
h 0
1 1 1
n n 1 1
i 1
Có thể bạn quan tâm!
-
 Bốc Xếp Trái Thanh Long Vận Chuyển Đến Nơi Tiêu Thụ
Bốc Xếp Trái Thanh Long Vận Chuyển Đến Nơi Tiêu Thụ -
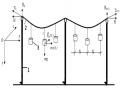
 Tời; 2- Dây Cáp Mang; 3- Dây Cáp Nâng Tải; 4- Xe Treo; 5. Dây Cáp Kéo Xe Treo
Tời; 2- Dây Cáp Mang; 3- Dây Cáp Nâng Tải; 4- Xe Treo; 5. Dây Cáp Kéo Xe Treo -
 Thông Số Kỹ Thuật Của Hệ Thống Đường Cáp Vận Chuyển Thanh Long
Thông Số Kỹ Thuật Của Hệ Thống Đường Cáp Vận Chuyển Thanh Long -
 Tính Toán Một Số Thông Số Cơ Học Của Dây Cáp Chịu Dãn, Trọng Tải Phân Bố Đều
Tính Toán Một Số Thông Số Cơ Học Của Dây Cáp Chịu Dãn, Trọng Tải Phân Bố Đều -
 Tính Phản Lực Tại Các Puli Đỡ Trong Hệ Thống Cáp Khép Kín
Tính Phản Lực Tại Các Puli Đỡ Trong Hệ Thống Cáp Khép Kín -
 Mô Hình Động Lực Học Của Các Giỏ Đựng Trái Thanh Long Trong Quá Trình Vận Chuyển Trên Ruộng Khi Thu Hái
Mô Hình Động Lực Học Của Các Giỏ Đựng Trái Thanh Long Trong Quá Trình Vận Chuyển Trên Ruộng Khi Thu Hái
Xem toàn bộ 196 trang tài liệu này.
xi
i
(0)
(0) (0) (0) (0)
n f
f2 (x h1,..., xn hn ) f2 (x ,..., xn
) 2
hi 0
(1.2)
1 1
............................
i 1 xi
n f
(0)
f (x(0) h ,..., x(0) h ) f (x(0) ,..., x(0) ) n
n
h 0
i
n 11 n n n 1
i 1
xi
Dẫn đến :
n f
(0)
1
h f (x(0) ,..., x(0) )
i 1
xi
i
(0)
1 1 n
n f
(0) (0)
2
hi f2 (x ,..., xn )
1
i 1
xi
(1.3)
n f
............................
(0)
n
h f (x(0) ,..., x(0) )
x
i n 1 n
i 1
f
i
(0)
Ở đây
k
xi
là đạo hàm riêng của hàm fk theo biến xi lấy tại điểm
X(0) (x(0) ,..., x(0) ) . Các giá trị h1, h2, ..., hn cần tìm.
1 n
Hệ (1.3) là hệ phương trình đại số tuyến tính nên giải được nghiệm:
Trong đó:
h(0)
J(0) 1 f (0)
(1.4)
f (X(0) ) f (X(0) )
f (X(0) )
1 1
x x
x(0)
1
x
1 2 n
1
f (X(0) )
f (X(0) )
f (X(0) )
(0)
![]()
2 2 2
(0)
(0)
x
2
[ J ]
x1
x2
xn
f
(0)
(1.5)
(0)
fn (X )
fn (X )
fn (X )
x(0)
(0)
x x
x n
1 2 n
do đó X(1)
X(0)
h(0)
Quá trính lặp theo công thức X(k 1)
X(k)h(k)
(1.6)
i 1
i
n
h
2
với độ chính xác được đánh giá :
- sai số cho trước. (1.7)
1.9.2. Phương pháp nghiên cứu thực nghiệm
Áp dụng các phương pháp đo lường các đại lượng không điện bằng điện để xác định các thông số đầu vào và xác định các thông số đầu ra.
Sử dụng các thiết bị đo và các phần mềm xử lý số liệu hiện đại để xác định các thông số phục vụ cho khảo sát bài toán lý thuyết như lực căng của dây cáp, độ vòng của đường cáp.
Quá trình tổ chức và tiến hành thí nghiệm xác định các đại lượng nghiên cứu được thực hiện theo phương pháp thống kê toán học và phương pháp thí nghiệm chuyên ngành [7]; [9].
Luận án sử dụng quy hoạch thực nghiệm với xử lý số liệu bằng phương pháp bình phương nhỏ nhất.
Quy hoạch thực nghiệm với xử lý số bằng phương pháp bình phương nhỏ nhất (BPNN)
Lý thuyết quy hoạch thực nghiệm dựa trền nền tảng của phương pháp bình
phương bé nhất. Giả sử đại lượng Y phụ thuộc vào các đại lượng x1 , x2 , ..., xk , tức là ứng với mỗi điểm Mi(x1, x2 , ..., xk) Rk ta có được giá trị thực nghiệm yi =
Y(Mi). Giá trị của các đại lượng x1, x2 , ..., xk ta có thể điều khiển được hoặc không điều khiển được.
Tại mỗi điểm Mi(x1, x2 ,.., xk)Rk ta có được giá trị thực nghiệm của đại
lượng yi = Y(Mi). Có thể nói đại lượng Y = F(x1 , x2 , ..., xk) với điều kiện các điểm M(x1 , x2 , ..., xk) D Rk , với D là miền đóng, bị chặn trong không gian Rk, do vậy mô hình thống kê ở đây là mô hình thống kê địa phương, tức là xét giá trị
các biến x1 , x2 , ..., xk trong một vùng nào đấy.
Do là mô hình địa phương nên ta có thể khai triển Taylor đối với hàm Y = F(x1 , x2 , ..., xk) dưới dạng :
k k
F(x1, x2 ,..., xk )
a0a jx jaijxix j ...
(1.8)
j1 i, j1
hay có dạng :
F(x1, x2 ,..., xk )
m
aifi(x1, x2,..., xk)
i 1
(1.9)
trong đó các hàm fi(x1 , x2 , ..., xk) ( với i = 1 m ) đã được biết.
Việc xác định các hệ số ai được dựa trên số liệu của n lần thực nghiệm, tức là tại n điểm Mj(x1, x2 , ..., xk) D (miền D là miền giới hạn của các biến xj) ta có được giá trị thực nghiệm của biến Y là yj , khi đó cần xác định các giá trị của ai
sao cho
n
j j
y
j1
F(M )2
min
n m 2
hay là : (a1,a2,...,am) yjaifi(x1, x2,..., xk)
min
(1.10)
j1 i 1
Các giá trị a1, a2, ..., am sẽ là nghiệm của hệ phương trình đại số :
a 0
1 (1.11)
![]()
a 0
m
n m
Trong đó:
a 2. yjaifi(M j) .fi(M j) , i 1 m
(1.12)
i j1 i1
aˆi
Hệ (1.11) là một hệ m phương trình đại số tuyến tính. Giải ra ta được các ai = và cho ta phương trình hồi quy thực nghiệm của hệ thống tương ứng với bộ n
thí nghiệm đã cho.
Hàm hồi quy thực nghiệm
Fˆ(x1, x2,..., xk)
m
aˆifi(x1, x2,..., xk)
i 1
Phương trình hồi quy thực nghiệm phụ thuộc vào bộ n thí nghiệm và phương pháp nhận dạng mô hình thống kê (tức là đưa ra các dạng hàm fi ). Như vậy cần phải có chiến lược tác động vào các yếu tố xj , xây dựng bộ n thí nghiệm sao cho
mô hình thu được đạt độ tin cậy đặt ra, đủ thông tin cần thiết, thuận tiện xử lý thông tin, tìm cực trị và dễ dạng sử dụng tính toán.
Nếu ta gọi véc tơ :
![]()
fi = ( fi(M1) , fi(M2) , ..., fi(Mn)) Rn
![]()
Y = ( y1 , y2 , ... , yn )
thì trong quá trình xác định các hệ số ai ta sẽ dẫn đến việc giải hệ phương
trình đại số tuyến tính A. aˆ
= B , trong đó : ma trận A = (aij) với
![]()
![]()
![]()
![]()
aij = < f i , f j > - là tích vô hướng hai véc tơ f i và f j ,
còn :
aˆ1
aˆ2
aˆ ;
![]()
b1
b2
B
![]()
![]()
![]()
với bi = < Y , f i > ;
aˆ
m
b
m
Bằng cách ký hiệu như trên ta nhận thấy ma trận A là ma trận đối xứng và
do hệ hàm { fi } là độc lập tuyến tính nên định thức det(A) 0
dẫn đến A khả
đảo và hệ phương trình A. aˆ
= B là hệ Cramer sẽ có duy nhất nghiệm ( aˆ 1 ,
aˆ 2,
..., aˆ m) vàaˆ
= A-1B
Nếu ta gọi ma trận F là ma trận có cột thứ i chính là các thành phần của
![]()
véc tơ fi
tức là :
![]()
f1 (M1) f2 (M1) fm (M1)
![]()
f1 (M2 ) f2 (M2 ) fm (M2 )
y1
y2
F =
![]()
và gọi Y =
![]()
f (M ) f (M ) f (M )
![]()
y
1 n 2 n m n n
![]()
![]()
![]()
khi đó FT là ma trận chuyển vị của F thì ta có được : A = FT.F và B = FT.Y với
Chú ý rằng họ véc tơ { f 1 , f 2 , ... , f m } là một họ véc tơ độc lập tuyến tính. Nếu là một họ trực giao, tức là :
< fi , fj > =
0 khi i j
i
2
khi i j
khi đó ma trận A sẽ là một ma trận chéo, dẫn đến:
2
aˆ i =bi
i
hay
aˆ i =
Y ,fi
2
i
với i 1m
![]()
![]()
![]()
Tính chất này được sử dụng trong phương pháp quy hoạch trực giao, khi mà ta có thể chủ động điều khiển được giá trị của các biến xj để có được hệ véc tơ {
f 1 , f 2 , ... , f m } là một họ véc tơ trực giao.
Kết luận chương 1
Từ những trình bày ở trên có thể đi đến một số kết luận:
1. Việt Nam có diện tích trồng thanh long lớn nhất châu Á, sản lượng thanh long xuất khẩu hàng đầu thế giới, chiến 49,8 % kim ngạch xuất khẩu trong nhóm trái cây ở Việt Nam.
2. Công nghệ và thiết bị thu hái vận chuyển trái thanh long sau thu hoạch còn nhiều tồn tại đó là năng suất thấp, trái thanh long bị tổn thương khi vận chuyển từ vườn trồng về nhà máy sơ chế, từ đó ảnh hưởng đến chất lượng sản phẩm khi xuất khẩu.
3. Các công trình nghiên cứu về đường cáp vận chuyển ở Việt Nam còn hạn chế, chưa có công trình nghiên cứu về đường cáp vận chuyển trái thanh long ở Việt Nam và trên thế giới được công bố.
4. Có nhiều công trình nghiên cứu về đường cáp vận chuyển gỗ được công bố, có thể sử dụng nguyên lý vận chuyển tuần hoàn và khép kín từ kết quả nghiên cứu đường cáp vận chuyển gỗ để nghiên cứu đường cáp vận chuyển trái thanh long. Mô hình đường cáp một dây chuyển động tuần hoàn liên tục phù hợp với việc vận chuyển trái thanh long.
Để có cơ sở lý thuyết cho quá trình tính toán thiết kế, hoàn thiện các thông số kỹ thuật của đường cáp vận chuyển trái thanh long, cũng như làm tài liệu tham khảo cho quá trình tính toán thiết kế cải tiến các đường cáp vận chuyển nông sản thì việc thực hiện đề tài: "Nghiên cứu động lực học của đường cáp vận chuyển trái thanh long ở vùng Tây Nam Bộ" mà đề tài luận án lựa chọn là cần thiết.
Chương 2
XÂY DỰNG MÔ HÌNH TÍNH TOÁN ĐỘNG LỰC HỌC CỦA ĐƯỜNG CÁP VẬN CHUYỂN TRÁI THANH LONG
Nội dung chính của chương này là xây dựng mô hình tính toán một số thông số cơ học, động lực học của đường cáp vận chuyển trái thanh long bao gồm:
- Bài toán thứ nhất là xây dựng mô hình tính toán thông số cơ học của đường cáp trong hai trường hợp:
+ Độ cao hai gối đỡ nhịp cáp bằng nhau;
+ Độ cao hai gối đỡ nhịp cáp có có độ chênh cao;
- Bài toán thứ hai là xây dựng mô hình động lực học của giỏ đựng trái thanh long khi cáp di chuyển cùng với sự tác động của lực gió và gia tốc chuyển động của giỏ chứa.
Phương pháp để nghiên cứu nội dung trên là sử dụng lý thuyết cơ học, lý thuyết mô hình hóa để xây dựng mô hình và thiết lập phương trình vi phân, sử dụng các phần mềm chuyên dùng để khảo sát các yếu tố ảnh hưởng đến các chỉ tiêu đánh giá, từ kết quả khảo sát rút ra những kết luận cần thiết. Sau đây luận án tiến hành xây dựng mô hình động lực học cho hai bài toán nêu trên.
2.1. Xây dựng mô hình tính toán cơ học đường dây cáp
Đề tài cấp nhà nước: Nghiên cứu thiết kế chế tạo một số thiết bị cơ giới hóa, tự động hóa một số khâu trong thu hoạch một số loại cây ăn quả tại vùng Tây Nam Bộ”, mã số KHCN-TNB/14-19/C30, đã thiết kế chế tạo ra hệ thống đường cáp vận chuyển trái thanh long như hình 2.1.

Hình 2.1. Sơ đồ đường cáp vận chuyển trái thanh long
Từ mô hình hệ thống đường cáp trên hình 2.1 và nguyên lý hoạt động của đường cáp, luận án lập mô hình tính toán đường cáp như trên hình 2.2.
Do cấu tạo đường cáp vận chuyển thanh long là một đường khép kín, cáp di chuyển với tốc độ chậm (0,1-0,3m/s) và được đỡ bởi các puli trên các trụ. Các giỏ đựng trái thanh long có trọng lượng 0.5 kg – 2 kg và được liên kết với cáp theo khoảng cách đều nhau (2 m). Chiều dài nhịp theo thiết kế từ 20- 25 m và yêu cầu độ vòng lớn nhất phải nhỏ hơn 0,4m. Dây cáp thiết kế là cáp thép đường kính 6mm, tải trọng tối dự án của dây cáp 15-20N/m.
Do tải được treo với khoảng cách đều trên dây cáp, nên luận án đặt giả thiết là tải trọng treo trên dây cáp là phân bố đều, bỏ qua trọng lượng dây cáp. Đây là giả thiết rất quan trọng, nó làm giảm thiểu rất nhiều cho độ phức tạp trong quá trình tính toán. Giả thiết này sẽ được kiểm chứng lại trong quá trình tính toán.
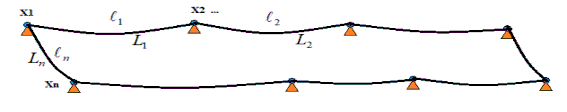
Hình 2.2. Sơ đồ tính toán đường cáp khép kín
Thông số dây cáp theo thiết kế như sau:
+ Đường kính dây cáp 6mm;
+ Cáp thép mạ kẽm loại 6 tao 12 sợi;
+ Lòi đay được làm từ xơ tổng hợp;
+ Xoắn kiểu RRL (Right Regular Lay). Loại FC – cáp lòi đay, tự bôi trơn bằng lượng mỡ tích trữ trong lòi;
+ Cáp có trọng lượng riêng : 90 N/100m
+ Lực kéo lớn nhất : 1470 N
+ Lực kéo đứt cáp : 12 KN
Như vậy, dây cáp được dùng cho hệ thống có trọng lượng trên 1m chiều dài nhỏ, do đó trong tính toán có thể bỏ qua sự dãn do trọng lượng bản thân.
Với các đặc điểm trên, có thể tính toán đường cáp theo mô hình với các giả
thiết:
+ Tải trọng phân bố đều (q) trên các nhịp ![]() ;
;
+ Bỏ qua sự dãn của dây do trọng lượng bản thân.
2.2. Tính toán một số thông số cơ học của dây cáp tựa trên các gối đỡ có cùng độ cao, chịu tải phân bố đều
2.2.1. Tính toán một số thông số cơ học của dây cáp không chịu dãn, tải trọng phân bố đều
Theo như phân tích ở trên, trong nội dung này ta xét bài toán dây mềm không chịu dãn, còn tải trọng là phân bố đều (q). Vì quá trình vận chuyển, có sự giới hạn về cường độ tải trọng (lực/độ dài) trên dây cáp q < qmax. Do vậy, tải trọng phân bố đều cường độ qmax là trường hợp dây chịu tải trọng lớn nhất. Chính vì vậy, tính toán cơ học cho dây trong trường hợp này là làm cơ cở để thiết kế độ bền các chi tiết của đường cáp, đảm bảo đường cáp vận hành an toàn và ổn định.
Đặt bài toán:
- Xét dây được giữ trên 2 gối ngang nhau với khoảng cách AB = ![]() .
.
- Dây có chiều dài L (m), trọng lượng riêng của dây cùng tải trọng theo chiều dài γ (N/m). Đặt P = γ. L.
- Giả thiết:
+ Trọng lượng bản thân của dây và tải trọng được phân bố đều trên dây cung
với cường độ q (N/m) =>
q P ;
![]()
+ Không tính đến sự dãn của dây do tải trọng.
2.2.1.1. Thiết lập phương trình độ vòng
Chọn hệ tọa độ Oxy: Gốc O trùng với một gối đỡ, trục Ox nối hai gối đỡ (ngang nhau), trục Oy hướng xuống dưới.
Gọi : T- Lực căng dây cáp;
H - Lực căng chiều theo phương ngang (gọi là lực căng ngang);
R- Lực căng chiếu theo phương thẳng đứng ( gọi là lực căng dọc); y - Độ vòng của dây => y = y(x);
f - Độ vòng lớn nhất của dây (tại điểm giữa dây do tải trọng phân bố đều).