Lựa chọn hệ thống bài tập, hướng dẫn giải và giải bài tập Vật lý (chương “Dòng điện xoay chiều” lớp 12 chương trình nâng cao) - 13

Đặt

y  R2  Z 2  1  2Z 1  1  ax2  bx  1

C Z 2 C Z

Với

x  1 ;

ZL

L L

C

a  R2  Z 2 ;

b  2ZC

UMBmax khi ymin

C

Vì a  R2  Z 2 > 0 nên tam thức bậc hai đạt cực tiểu khi

x   b

2a

hay

1  

ZL

2ZC

C

2R2  Z 2 

 ZC R2  Z 2

� ZL 

R2  Z 2

C

C

ZC

 1002  1002  200

100

� L  ZL



 200  2 H 100 

Hệ số công suất:

R  Z  Z

2



L C



2

cos  R 

100

1002  200 1002

 2

2

Cách 3: Phương pháp dùng giản đồ Fre­nen.

Dung kháng:

U L

P

U

O



1

U

R

U1



C Q

Z  1  1  100

C C

100 .

104



U  U R  UC  U L Đặt U1  U R  UC Ta có:

1

tan  UC

 IZC

 ZC

 100  1

U R IR R 100



I

� 1  4 rad

Vì      �     

1 2

�       

2 4 4

2 1

U

rad

Xét tam giác OPQ và đặt

    1 .

Theo định lý hàm số sin, ta có:

U 

sin

U L

sin 

�U L

 U sin 

sin

Vì U và sin không đổi nên ULmax

khi sin cực đại hay sin

= 1�   

2

Vì      �     

  

rad.

1 1 

 

2 4 4

Hệ số công suất:

cos  cos   2

4 2

Mặt khác, ta có:

tan  ZL  ZC

R

 1 � Z

L  ZC

 R  100  100  200

Bài 2: Tóm tắt:

R = 100

L = 0,318H

C thay đổi

� L  ZL



 200  2 H 100 

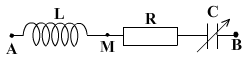
u  200 2 cos100 t (V)

a. C = ? để UCmax. Tính UCmax = ?

b. C = ? để UMBmax . Tính UMBmax.

Các mối liên hệ cần xác lập:

­ Biểu thức tính cảm kháng: ZL  L

Tìm C để UCmax:

UZC

R  Z  Z

2



L

C



2



R  Z1  2Z1  1

2 2

L



ZC

2

L

ZC

y

U

U

Cách 1: Phương pháp đạo hàm

U

­ Ta có:

C  IZC   

­ Đặt

y  R2  Z 2  1  2Z

1  1  R2  Z 2 x2  2x.Z

 1 (với

x  1 )

L Z 2 L Z L L Z

­ UCmax khi ymin.

­ Khảo sát hàm số

C C C

L L

L L

y  R2  Z 2 x2  2x.Z  1

Lấy đạo hàm y’ theo x:

y '  2R2  Z 2 x  2Z

y '  0

� 2R2  Z 2 x  2Z  0

� x 

ZL

L

R2  Z 2

� y 

R2

L

R2  Z 2

L L

Bảng biến thiên:

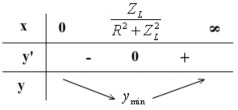
x  ZL

1  ZL � Z  R2  Z 2

� C  1

ymin khi

R2  Z 2

hay

L

L

C L

L

Z R2  Z 2 C Z

ZC

U

­

C max

 U R2  Z 2

L

R

UZC

R  Z  Z

2



L

C



2

y

U

U

Cách 2: Phương pháp dùng tam thức bậc hai.

U

­ Ta có:

C  IZC   



R  Z1  2Z1  1

2

2

L



ZC

2

L

ZC

­ Đặt

y  R2  Z 2  1  2Z 1  1  ax2  bx  1

L Z 2 L Z

C C

(với

x  1 ;

ZC

a  R2  Z 2 ;

b  2ZL )

L

­ UCmax khi ymin. Vì hàm số y có hệ số góc a > 0, nên y đạt cực tiểu khi

x   b

hay

1  ZL

� ZC

2a

L

 R2  Z 2

ZL

Z R2  Z 2

C L

C

U

­

C max

 U R2  Z 2

U1



P



U R

I

U

Q

L

R U

L

Cách 3: Phương pháp dùng giản đồ Fre­nen.

­ Vẽ giản đồ Fre­nen. Đặt U1  U L  U R

­ Áp dụng định lý hàm số sin:

U 

sin

UC

sin 

�UC

 U sin  O

sin

U R

­ Vì U và

sin  R 

U1

không đổi, nên

R2  Z 2

L

U

UCmax khi sin  đạt giá trị cực đại, hay sin   1 C

�UC max

 U R2  Z 2

L

R

­ Khi sin   1 �   

2

, ta có:

UUZ Z Z 2 R2  Z 2 1

cos  L  1 � L

U1 UC Z1

 1 � ZC  1 

ZC ZL

L � C 

Z

ZL C

Tìm C để UMBmax.

­ Lập biểu thức:

UZMB

R2  Z 2  2Z Z  Z 2

L

L C C

Z 2  2Z Z

L

L

R2  Z 2

C  1

C

y

U

U

UMB  IZMB   

y  Z 2  2Z Z  1  Z 2  2Z x  1

Đặt

L L C L L

(với x = ZC)

­ UMBmax khi ymin.

­ Khảo sát hàm số y:

R2  Z 2 R2  x2

C

2Z x2  x.Z

 R2 

+ Lấy đạo hàm y’ theo x:

y ' 

L L

R2  x2 2

L

y '  0 � x2  xZ  R2  0

L L

Z 2  4R2

Z

(*)



+ Giải phương trình (*)

x 

2

(x lấy giá trị dương)

Z

C

Z điện dung C  1

C

+ Lập bảng biến thiên:

U

+

MB max

 U 

U ZL  

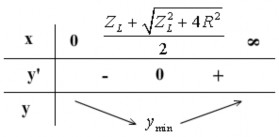
Z 2  4R2

L

2R

ymin

Tiến trình hướng dẫn học sinh giải:

Hoạt động của giáo viên

Hoạt động của học sinh
a. Tìm C để UCmax. UCmax = ?

Có thể bạn quan tâm!

• Dạng 5: Công Suất Của Đoạn Mạch R, L, C Mắc Nối Tiếp
• Dạng 6: Xác Định Giá Trị Cực Đại Của Điện Áp Hiệu Dụng Khi Thay Đổi L, Hoặc C, Hoặc F.
• Bài Tập Về Xác Định Giá Trị Cực Đại Umax Khi Thay Đổi L, Hoặc C, Hoặc F. Bài 1
• Dạng 7: Xác Định Các Phần Tử Điện R, L, C Chứa Trong Hộp Đen.
• Dạng 8: Giải Toán Nhờ Giản Đồ Vec­tơ.
• Lựa chọn hệ thống bài tập, hướng dẫn giải và giải bài tập Vật lý (chương “Dòng điện xoay chiều” lớp 12 chương trình nâng cao) - 16

Xem toàn bộ 169 trang tài liệu này.

­ Biểu thức tính cảm kháng.

Cách 1: Phương pháp đạo hàm

­ Lập biểu thức tính điện áp hiệu

­ ZL  L

UZ

dụng giữa hai đầu bản tụ.

­ UC  IZC 

C

R2  Z  Z 2

L C

 U

R2  Z 2  1  2Z

1  1

L Z 2 L Z

C C

­ Điện áp giữa hai đầu bản tụ UC đạt giá trị cực đại khi nào?

­ UCmax khi mẫu số tiểu.

đạt giá trị

cực

­ Đặt

y  R2  Z 2  1  2Z

1  1

L Z 2 L Z

C C

L L

 R2  Z 2 x2  2Z x  1

(với

x  1 )

ZC

­ Các bước khảo sát hàm số:

­ Các bước khảo sát một hàm số y theo x là gì?

­ Yêu cầu học sinh khảo sát hàm số y.

+ Lấy đạo hàm y’ theo x.

+ Tìm điểm cực trị tại y’ = 0.

+ Lập bảng biến thiên tìm điểm cực tiểu.

­ Khảo sát hàm số y:

+ Lấy đạo hàm y’ theo x:

L L

� y '  2R2  Z 2 x  2Z

L L

y '  0 2R2  Z 2 x  2Z  0

� x 

ZL

L

R2  Z 2

+ Bảng biến thiên:

x  1  Z � Z

 R2  Z 2

­ L L

L

­ Vậy y

khi

x  ZL

. Từ dữ

Z R2  Z 2 C Z

min

R2  Z 2

C L L

kiện này, hãy tìm C và UCmax.

� C  1

ZC

UC max

 U R2  Z 2

L

R

Cách 2: Phương pháp dùng tam thức bậc hai.

­ Bước 1 và 2 tương tự như trên.

­ Đặt

y  R2  Z 2  1  2Z

1  1

L Z 2 L Z

C C

 ax2  bx  1

(với x  1 ; a  R2  Z 2 ; b  2Z )

L

­ Vì a > 0 nên ymin khi

x   b (*)

ZC L 2a

­ Tam thức bậc hai y đạt cực tiểu khi nào?

­ Thay các giá trị a, b và x vào biểu

thức (*) ZC C và UCmax.

Cách 3: Phương pháp dùng giản

­ U  U  U  U

đồ vec­tơ.

­ Hãy viết biểu thức điện áp hiệu dụng toàn mạch dưới dạng vectơ.

L R C

­ Đặt U1  U L  U R .

­ Vẽ giản đồ Fre­nen.

U 

sin

UC

sin 

�UC

 U sin 

sin

U L  P

­ Vì U và

sin  U R 

U1

R

L

R2  Z 2



U1 không đổi nên UCmax khi sin cực đại hay sin = 1.

O  ­ Khi sin   1 �   2

U R I

U U Z Z

U

� cos  L

U1

 1 � L  1

UC Z1 ZC

1

Z

C

U

Q � Z  Z 2 

C

L

R2  Z 2

L

ZL

� C 

1

ZC

­

Áp dụng định lý hàm số sin đối với

�UC max

 U R2  Z 2

L

R

UZ

2 góc , như UC?

trên hình, hãy tìm

­ UMB  IZMB 

2

R

MB

2

 ZL  ZC 

­ UC đạt giá trị cực đại khi nào?

 U R2  Z 2

C

R2  Z 2  2Z Z

 Z 2

L L C C

L L C

 U

­ Từ

lý luận đó, hãy tính C và

Z 2  2Z Z  1

C

R2  Z 2

(**)

UCmax.

­ UMBmax khi mẫu số của biểu thức

(**) đạt giá trị cực tiểu.

­ Khảo sát hàm số y:

+ Lấy đạo hàm y’ theo x:

L L

2Z x2  x.Z  R2 

b. Tìm C để UMBmax. UMBmax = ?

­ Hãy lập biểu thức tính điện áp hiệu dụng giữa hai điểm M, B và

y ' 

R2  x2 2

khai triển nó.

+ y '  0 � x2  xZ

 R2  0

L

Giải phương trình:

Z  Z 2  4R2

(lấy

x  0 )

� x  L L

2

+ Lập bảng biến thiên:

­ UMBmax khi nào?

y  Z 2  2Z Z  1

­ Đặt

L L C

C

R2  Z 2

2

U  IZ  UZC

L C

x  Z  Z  4R

2 2

 ZL  2ZL x  1 (với x  Z )

R2  x2 C

C C R2  Z  Z 2 khi

L L

2

­ Để

tìm giá trị

cực tiểu của hàm

Hay

Z  Z 2  4R2 1

số y

ta khảo sát hàm số

y. Yêu

Z  L L � C 

C 2

ZC

cầu học sinh khảo sát hàm số y và tìm C, UMBmax.

Thay x vào y, suy ra:

y  4R2

L L

min  Z 2  4R2  Z 2



U U Z  Z 2  4R2 

Bài giải:

a. Tính C để UCmax.

UMB max 

L L

ymin 2R

Cảm kháng :

ZL  L  100 .0,318  100

UZC

R  Z  Z

2



L

C



2



R  Z1  2Z1  1

2 2

L



ZC

2

L

ZC

y

U

U

Cách 1: Phương pháp đạo hàm:

U

Ta có:

C  IZC   

Đặt

y  R2  Z 2  1  2Z

1  1  R2  Z 2 x2  2x.Z

 1 (với

x  1 )

L Z 2 L Z L L Z

UCmax khi ymin. Khảo sát hàm số:

C C C

L L

y  R2  Z 2 x2  2x.Z  1

L L

L L

� y '  2R2  Z 2 x  2Z

y '  0

� 2R2  Z 2 x  2Z  0

� x 

ZL

L

R2  Z 2