UZC
U
R Z Z
2
L
C
2
R
2
Z
2
L
1
ZC
2 2ZL 1
1
ZC
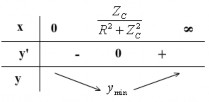
y
U
UC IZC
Tương tự như trên, dùng ba phương pháp: đạo hàm, tam thức bậc hai, và giản đồ Frenen để giải.
Ta có kết quả: U
C max
U R2 Z 2 và
L
R
ZC
R2 Z 2
L
ZL
Chú ý: Nếu tìm điện áp cực đại ở hai đầu đoạn mạch nhỏ gồm R nối
y
U
tiếp C thì lập biểu thức thiên để tìm ymin.
U RC
và dùng đạo hàm, lập bảng biến
Xác định giá trị cực đại ULmax, và UCmax khi tần số f thay đổi:
Lập biểu thức:
U L IZL
UZL U U
1 1
L2C 2 4
. R
�
�
2
�
2
L
� 1
C �L
�2 2
1
y
2
R2 �L 1 �
� C �
� �
Đặt
a 1 ,
b �R2 2L �1 ,
c 1 ,
x 1
� y ax2 bx c
L2C 2
� C �L2 2
� �
Lập biểu thức:
UC IZC
U U U
L C C R
2 2 4 2
�
�
2
2L�
1
2
�
C �
�
y
2
C R2 �L 1 �
� C �
Đặt
a L2C 2 ,
� �
b C2 �R2 2L �
c 1
, x 2
� y ax2 bx c
� C �,
� �
Dùng tam thức bậc hai của ẩn phụ x để tìm giá trị cực tiểu của y, cuối cùng có chung kết quả:
U
2
2L R2
C
1
L max
UC max
2LU R
4LC R2C 2
,
1
2L R2
L 2
oL C
oC L
C(với điều kiện 2 C R ) 2
Các trường hợp linh hoạt sử dụng các công thức hoặc vẽ giản đồ Fre nen để giải toán.
6.2. Bài tập về xác định giá trị cực đại Umax khi thay đổi L, hoặc C, hoặc f. Bài 1
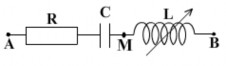
Cho mạch điện như hình vẽ. Điện áp
giữa hai đầu AB ổn định có biểu thức
u 200cos100 t (V). Cuộn dây thuần cảm
kháng có độ
tự cảm L thay đổi được, điện
104
trở R = 100
, tụ điện có điện dung C (F). Xác định L sao cho điện áp
đo được giữa hai điểm M và B đạt giá trị cực đại, tính hệ số công suất của mạch điện khi đó.
Bài 2
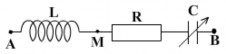
Mạch điện như hình vẽ. Cuộn dây thuần
cảm có độ tự cảm L = 0,318H, R = 100 , tụ
C là tụ xoay. Điện áp đặt vào hai đầu đoạn
![]()
mạch có biểu thức u 200 2 cos100 t (V).
a. Tìm C để điện áp giữa hai đầu bản tụ đạt giá trị cực đại, tính giá trị cực đại đó.
b. Tìm C để điện áp hai đầu MB đạt cực đại, tính giá trị cực đại đó.
Bài 3
![]()
2
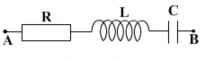
Cho mạch điện xoay chiều như hình vẽ. Đặt vào hai đầu đoạn mạch AB một điện áp uAB 100 3 cost (V) ( thay đổi được). Khi
1
thì UR = 100V ;
UC 50
V ; P = 50
W. Cho
L 1 H và
6
UL > UC. Tính UL và chứng tỏ đó là giá trị cực đại của UL.
6.3. Hướng dẫn giải và giải: Bài 1:
Tóm tắt:
u 200cos100 t (V) L thay đổi
R = 100
104 F
C
L = ? để UMBmax. cos = ?
Các mối liên hệ cần xác lập:
Áp dụng công thức tính dung kháng
Z 1
C C
Cách 1: Dùng phương pháp đạo hàm
U AB ZL
U AB
R Z Z
2
L
C
2
R
2
Z
2
C
1
ZL
2 2ZC 1
1
ZL
U AB
y
UMB IZL
Đặt
y R2 Z 2 1 2Z
1 1 R2 Z 2 x2 2Z
.x 1(với
x 1 )
C Z 2 C Z C C Z
UMBmax khi ymin
Khảo sát hàm số
L L L
C C
y R2 Z 2 x2 2Z x 1
C C
y ' 2R2 Z 2 x 2Z
C C
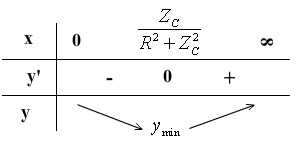
y ' 0 � 2R2 Z 2 x 2Z Bảng biến thiên:
0 � x
ZC
C
R2 Z 2
ymin khi
x ZC
R2 Z 2
hay
1 ZC
Z R2 Z 2
� ZL
R2 Z 2
� L ZL
C
C L C
ZC
Áp dụng công thức tính hệ số công suất
cos R
R Z Z
2
L C
2
U AB ZL
R Z Z
2
L
C
2
U AB
R Z1 2Z
2
2
C
ZL
2
C
1 1
ZL
U AB
y
Cách 2: Phương pháp dùng tam thức bậc hai
UMB IZL
Đặt
y R2 Z 2 1 2Z 1 1 ax2 bx 1
C Z 2 C Z
Với
x 1 ;
ZL
L L
C
a R2 Z 2 ;
b 2ZC
UMBmax khi ymin
Vì a > 0 nên tam thức bậc hai y đạt cực tiểu khi
x b
2a
hay
1 2ZC
C
ZL 2R2 Z 2
ZC R2 Z 2
� ZL
R2 Z 2
C
ZC
� L ZL
C
Áp dụng công thức tính hệ số công suất của mạch:
R Z Z
2
L C
2
cos R
Cách 3: Phương pháp dùng giản đồ Frenen
Vẽ giản đồ Frenen.
U
1
U
R
U1
U L
O I
UC
U U L UC U R . Đặt U1 U R UC
tan
UC
IZC
ZC
1
1
U R IR R
2 1
Đặt
1 .
Áp dụng định lý hàm số sin:
U
sin
U L
sin
�U L
U sin
sin
Vì U và sin có giá trị
không đổi nên để
ULmax khi sin cực đại hay
sin 1 �
2
rad giá trị hệ số công suất cos
, ZL và L.
Tiến trình hướng dẫn học sinh giải:
Cách 1: Dùng phương pháp đạo hàm
Hoạt động của học sinh | |
Biểu thức tính dung kháng. Hãy lập biểu thức tính điện áp hiệu dụng giữa hai đầu cuộn dây theo định Ohm và khai triển nó. Dựa vào biểu thức (1), UMBmax khi nào? Đặt y R2 Z 2 1 2Z 1 1 C Z 2 C Z L L R2 Z 2 x2 2Z .x 1 C C (với x 1 ) ZL Các bước để khảo sát một hàm số y theo x là gì? Yêu cầu học sinh khảo sát hàm số y. ymin khi nào? Từ đó tính ZL và L? | Z 1 C C U IZ U AB ZL MB L R2 Z Z 2 L C U AB R2 Z 2 1 2Z 1 1 (1) C Z 2 C Z L L UMBmax khi mẫu số min Các bước để khảo sát hàm số y theo x là: + Lấy đạo hàm y’ theo x. + Xét cực trị khi y’ = 0. + Lập bảng biến thiên. y ' 2R2 Z 2 x 2Z C C y ' 0 � 2R2 Z 2 x 2Z 0 C C � x ZC R2 Z 2 C Bảng biến thiên:
y khi x ZC min R2 Z 2 C 1 ZC � Z R2 Z 2 Hay Z R2 Z 2 L C L C ZC |
Có thể bạn quan tâm!
-
 Dang 4: Xác Định Các Đại Lượng Điện Khi Biết Hai Đoạn Mạch Có Điện Áp Cùng Pha, Vuông Pha.
Dang 4: Xác Định Các Đại Lượng Điện Khi Biết Hai Đoạn Mạch Có Điện Áp Cùng Pha, Vuông Pha. -
 Dạng 5: Công Suất Của Đoạn Mạch R, L, C Mắc Nối Tiếp
Dạng 5: Công Suất Của Đoạn Mạch R, L, C Mắc Nối Tiếp -
 Dạng 6: Xác Định Giá Trị Cực Đại Của Điện Áp Hiệu Dụng Khi Thay Đổi L, Hoặc C, Hoặc F.
Dạng 6: Xác Định Giá Trị Cực Đại Của Điện Áp Hiệu Dụng Khi Thay Đổi L, Hoặc C, Hoặc F. -
 Lựa chọn hệ thống bài tập, hướng dẫn giải và giải bài tập Vật lý (chương “Dòng điện xoay chiều” lớp 12 chương trình nâng cao) - 13
Lựa chọn hệ thống bài tập, hướng dẫn giải và giải bài tập Vật lý (chương “Dòng điện xoay chiều” lớp 12 chương trình nâng cao) - 13 -
 Dạng 7: Xác Định Các Phần Tử Điện R, L, C Chứa Trong Hộp Đen.
Dạng 7: Xác Định Các Phần Tử Điện R, L, C Chứa Trong Hộp Đen. -
 Dạng 8: Giải Toán Nhờ Giản Đồ Vectơ.
Dạng 8: Giải Toán Nhờ Giản Đồ Vectơ.
Xem toàn bộ 169 trang tài liệu này.

� L ZL cos R R2 Z Z 2 L C |
Cách 2: Phương pháp dùng tam thức bậc hai
Hoạt động của học sinh | |
Biểu thức tính dung kháng. Hãy lập biểu thức tính điện áp hiệu dụng giữa hai đầu cuộn dây theo định Ohm và khai triển nó. Dựa vào biểu thức (1), UMBmax khi nào? Đặt y R2 Z 2 1 2Z 1 1 C Z 2 C Z L L ax2 bx 1 (với x 1 ; a R2 Z 2 ; b 2Z ) Z C C L Tam thức bậc hai y đạt cực tiểu khi nào? Thay số vào biểu thức (2) ZL và L. Biểu thức tính hệ số công suất. | Z 1 C C U IZ U AB ZL MB L R2 Z Z 2 L C U AB R2 Z 2 1 2Z 1 1 (1) C Z 2 C Z L L UMBmax khi mẫu số min Vì hệ số góc a R2 Z 2 > 0, nên C tam thức bậc hai y đạt cực tiểu khi x b (2) 2a cos R R2 Z Z 2 L C |
Cách 3: Phương pháp dùng giản đồ Frenen
Hoạt động của học sinh | |
Hãy viết biểu thức điện áp hiệu dụng toàn mạch dưới dạng vectơ. Đặt U1 U R UC . | U U R UC U L |
I Z 1 C C tan UC IZC ZC 1 U IR R 1 R Vì � 1 2 2 1 Theo định lý hàm số sin, ta có: U U L �U U sin sin sin L sin ULmax khi sin cực đại hay sin 1 � 2 1 tan ZL ZC ��Z L R L |
Vẽ giản đồ Frenen.
Bài giải:
Cách 1: Phương pháp đạo hàm
Z 1 1 100
Dung kháng:
C C
100 .
104
Ta có:
UMB IZL
U AB ZL
U AB
R Z Z
2
L
C
2
R
2
Z
2
C
1
ZL
2 2ZC 1
1
ZL
Đặt
y R2 Z 2 1 2Z
1 1 R2 Z 2 x2 2Z
.x 1(với
x 1 )
U AB
y
C Z 2 C Z C C Z
L L L
UMBmax khi ymin. Khảo sát hàm số y:
C C
Ta có: y ' 2R2 Z 2 x 2Z
C C
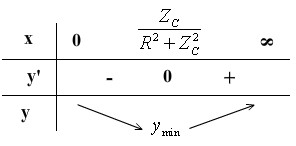
y ' 0 � 2R2 Z 2 x 2Z Bảng biến thiên:
0 � x
ZC
C
R2 Z 2
C
y khi x ZC
L C
hay
1 ZC
min
� ZL
R2 Z 2
C
R2 Z 2
ZC
Z R2 Z 2
1002 1002 200
100
� L ZL
Hệ số công suất:
R Z Z
2
L C
2
cos
200 2 H 100
R
100
1002 200 1002
2
2
Cách 2: Phương pháp dùng tam thức bậc hai
Z 1 1 100
Dung kháng:
C C
100 .
104
U AB ZL
U AB
R Z Z
2
L
C
2
R
2
Z
2
C
1
ZL
2 2ZC 1
1
ZL
U AB
y
Ta có:
UMB IZL