Dạng 7: Xác Định Các Phần Tử Điện R, L, C Chứa Trong Hộp Đen.

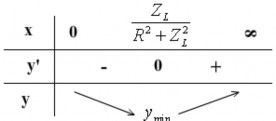
Bảng biến thiên:

L

y khi x  ZL

C L

hay

1  ZL

min

R2  Z 2

Z R2  Z 2

� ZC 

R2  Z 2

L

ZL

 1002  1002  200

100

1 1 5.105

C

� C  Z

  F 100 .200 

U R2  Z 2 200

(V)

1002  1002

2

U  L   200

C max R

100

UZC

R  Z  Z

2



L

C



2

y

U

U

Cách 2: Phương pháp dùng tam thức bậc hai.

U

Ta có:

C  IZC   



R  Z1  2Z1  1

2

2

L



ZC

2

L

ZC

Đặt

y  R2  Z 2  1  2Z 1  1  ax2  bx  1

L Z 2 L Z

C C

(với

x  1

ZC

; a  R2  Z 2

; b  2ZL )

L

UCmax khi ymin. Vì hàm số y có hệ số góc a > 0, nên y đạt cực tiểu khi

x   b

hay

1  ZL

2a

L

� ZC 

R2  Z 2

Z R2  Z 2

C L

 1002  1002  200          

U1



P



U R

I

U

Q

ZL 100 U

1 1 104 L

C

� C  Z

 

100 .200 2

(F).

1002  1002

2

U R2  Z 2 200 V

U  L   200

C max R

100 O

Cách 3: Phương pháp dùng giản đồ Fre­nen.

Ta có: U  U  U  U

L R C

Áp dụng định lý hàm số sin, ta có:

UC

U 

sin

UC

sin 

�UC

 U sin 

sin

Vì U và sin = 1.

sin  U R  R

R2  Z 2

L

U1

không đổi nên U

Cmax

khi sin cực đại hay

Khi sin   1 �   

2

� cos  U L

U1

 U1

UC

� ZL

Z1

 Z1 ZC

Z

2

� ZC  1

ZL

 R2  Z 2

L

ZL

 1002  1002  200

100

1 1 5.105

C

� C  Z

  F 100 .200 

U R2  Z 2 200

(V)

1002  1002

2

U  L   200

C max R

100

b. Tìm C để UMbmax. UMBmax = ? Lập biểu thức:

UZMB

R2  Z 2  2Z Z  Z 2

L

L C C

Z 2  2Z Z

L

L

R2  Z 2

C  1

C

y

U

U

UMB  IZMB   

y  Z 2  2Z Z  1  Z 2  2Z x  1

Đặt

L L C L L

(với x = ZC)

C

R2  Z 2 R2  x2

UMBmax khi ymin.

Khảo sát hàm số y:

y ' 

2Z x2  x.Z

 R2 

L L

R2  x2 2

L

y '  0 � x2  xZ  R2  0

(*)

Giải phương trình (*)

x  ZC

 Z 

L L

Z 2  4R2

2

(x lấy giá trị dương).

� ZC

 1002 

1002  4.1002

2

 501 

5  162

Lập bảng biến thiên:

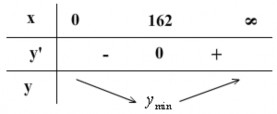
điện dung C  1  1  0,197.104 F

Thay

x  ZC

 Z

ZC

L L

Z 2  4R2



2

100 .162

vào biểu thức y

� y 

4R2 

4R  2Z  2Z

2

2

Z  4R

2

2

L

L L

min 2



4R2

 ZL 

Z  4R

2

2

L

Z 2  4R2

L

1002  4.1002

U U Z   200100  

L

ymin

UMB max   2R

  324 (V)

2.100

Bài 3: Tóm tắt:

uAB  100 3 cost

 thay đổi

  1

U R  100 V

UC  50 2 V

P = 50 6 W

L  1 H



UL > UC

(V)

UL = ? Chứng tỏ ULmax.

Các mối liên hệ cần xác lập:

­ Điện áp hiệu dụng toàn mạch: U 2  U 2  U

 U 2

giá trị của U .

R L C L

­ Công suất tiêu thụ toàn mạch:

P  UI cos  UI

(vì   0 ) � I  P

U

­ Từ biểu thức định luật Ohm giá trị của điện trở R, ZL và ZC.

­ ZL

 1L � 1

 ZL

L

� C  1

 .Z

1 C

­ Chứng tỏ ULmax:

+ Lập biểu thức tính điện áp hiệu dụng giữa hai đầu cuộn dây:

R  L 

2

�

�

1

�

C �

�

2

�

U L  IZL 

UL  U  U

1

L2C 2 4

 R  2

�

�

2

L � 1

�

C �L 

�2 2

 1

y

Đặt

y  1  �R2  2 L � 1  1  ax2  bx  1

L2C 24 �

C �L22

� �

Với

x  1

; a  1

; b  �R2  2 L �1

 2 L2C 2

� C �L2

� �

+ ULmax khi ymin. Tam thức bậc hai y đạt cực tiểu khi

x   b

2a

(vì a > 0).

+ ymin

   

U

4a

R2

4L2

4LC  R2C 2 

ymin

+ U L max 

 2UL giá trị U

4LC  C 2 R2

R L

đã tính ở trên khi   1 .

Tiến trình hướng dẫn học sinh giải:

Hoạt động của giáo viên

Hoạt động của học sinh
­ Biểu thức tính điện áp hiệu dụng	­ U 2  U 2  U  U 2 . Vì U > U R L C L C nên �U  U  U 2  U 2 (*) L C R Thay giá trị của U, UR, UC vào biểu thức (*) giá trị của UL. ­ = 0. ­ P  UI cos  UI (vì = 0) � I  P U ­ R  U R ; Z  U L ; Z  UC I L I C I ­ Z   L �   ZL ; C  1 L 1 1 L 1ZC ­ U  IZ  UZL L L R2  Z  Z 2 L C
toàn mạch. Từ đó tính điện áp hiệu
dụng hai đầu cuộn dây.
­ Theo bài, độ lệch pha có giá trị
bao nhiêu?
­ Biểu thức tính cường độ dòng
điện trong mạch khi biết công suất
P và điện áp hiệu dụng U.
­ Từ biểu thức định luật Ohm, hãy
tính điện trở R, cảm kháng ZL,
dung kháng ZC.
­ Hãy tính tần số 1 khi có ZL và L.
Từ đó tính điện dung C của tụ
điện.
­ Để chứng tỏ UL cực đại khi
  1 ta tìm ULmax và so sánh với
UL, nếu ULmax = UL thì giá trị UL
tính ở trên là giá trị cực đại.
­ Lập biểu thức tính điện áp hiệu

Có thể bạn quan tâm!

• Dạng 6: Xác Định Giá Trị Cực Đại Của Điện Áp Hiệu Dụng Khi Thay Đổi L, Hoặc C, Hoặc F.
• Bài Tập Về Xác Định Giá Trị Cực Đại Umax Khi Thay Đổi L, Hoặc C, Hoặc F. Bài 1
• Lựa chọn hệ thống bài tập, hướng dẫn giải và giải bài tập Vật lý (chương “Dòng điện xoay chiều” lớp 12 chương trình nâng cao) - 13
• Dạng 8: Giải Toán Nhờ Giản Đồ Vec­tơ.
• Lựa chọn hệ thống bài tập, hướng dẫn giải và giải bài tập Vật lý (chương “Dòng điện xoay chiều” lớp 12 chương trình nâng cao) - 16
• Bài Tập Về Máy Phát Điện Và Động Cơ Điện: Bài 1

Xem toàn bộ 169 trang tài liệu này.

dụng hai đầu cuộn dây theo định luật Ohm và khai triển nó.

 UL

�

R2  �L 

�



1 �2

�

C �

U

1  �R2  2 L� 1  1

L2C 24 �

C �L2 2

� �

­ Đặt:

y  1  �R2  2 L � 1  1

L2C 24 �

C �L22

� �

 ax2  bx  1

(với

x  1 ;

 2

a  1 ; b  �R2  2 L �1 )

L2C 2 � C �L2

U khi y .

� � ­

L max

min

­ ULmax khi nào?

­ Điều kiện để tam thức bậc hai y

­ Vì hệ số a > 0 nên tam thức bậc hai

b

đạt cực tiểu là gì?

y đạt cực tiểu khi

x  

2a

(**)

­ Hãy tính ymin và ULmax.

­   R4 �1

�L4

�

 4

L3C

� ymin

   

4a

R2

4L2

4LC  R2C 2 

�U  U

 2UL

Bài giải:

Ta có: U 2  U 2  U  U 2

L max

ymin R

4LC  C 2 R2

R L C

Thay các giá trị của U, UR, UC ta được:

2

L L

50 6 2  1002  U  50 2 2 �U  100

(V)

0 6

Công suất tiêu thụ toàn mạch:

P  UI cos  UI

(vì   0 ) � I  P  5

U 50

 1A

6

� R  U R

I

 100  100 1

0 2

U 10

�   ZL

 10

 100

2

rad/s

ZL 

L   100 2 1 L 1

I 1 

0 2

U 50 2

1 1 104

2

ZC  C   50 2 � C   Z



100

2.50

  F

I 1 1 C

y

Ta có:

R  L 

2

�

�

1

�

C �

�

2

�

U L  IZL 

UL  U  U

1

L2C 2 4

 R  2

�

�

2

L � 1

�

C �L 

�2 2

 1

Đặt

y  1  �R2  2 L � 1  1  ax2  bx  1

L2C 24 �

C �L22

� �

Với

x  1

; a  1

; b  �R2  2 L �1

 2 L2C 2

� C �L2

� �

ULmax khi ymin. Tam thức bậc hai y đạt cực tiểu khi

x   b

2a

(vì a > 0).

�4

  b2  4ac  R4 �1

L

4 �



L3C �

� ymin

   

4a

R2

4L2

� �

4LC  R2C 2 

U 2UL

2.50 6. 1

�U L max

    

ymin

4LC  C 2 R2

4. .

1 104 �104 �2

  �

 � �.1002

�

R

2

 100

(V)

100

2

Vậy U L  U L max  100

(V).

7. Dạng 7: XÁC ĐỊNH CÁC PHẦN TỬ ĐIỆN R, L, C CHỨA TRONG HỘP ĐEN.

7.1. Phương pháp giải chung:

 Vẽ giản đồ Fre­nen nếu cần thiết.

 Dựa vào dữ kiện bài cho, độ lệch pha, vận dụng các quy luật của dòng

điện xoay chiều, tính toán và suy luận để trong hộp kín đó.

 Chú ý các trường hợp sau:

xác định được các phần tử

chứa

Nếu u và i cùng pha thì trong hộp đen có duy nhất một điện trở R hay có đủ ba phần tử điện R, L, C nhưng ZL = ZC.

Nếu u và i vuông pha nhau thì trong hộp đen không có điện trở thuần, có cuộn dây tự cảm L, có tụ điện C hoặc có cả hai.

Nếu u sớm pha hơn i một góc nhọn thì trong mạch có điện trở cuộn dây tự cảm L, hoặc cả ba phần tử điện R, L, C nhưng ZL > ZC.

R và

Nếu u chậm pha hơn i một góc nhọn thì trong hộp đen có điện trở và tụ điện, hoặc có cả ba phần tử điện R, L, C nhưng ZC > ZL.

 Các kiến thức dùng để tính toán định lượng: để giải bài toán về hộp đen ta phải vận dụng nhiều dạng bài tập đã trình bày ở trên, và dựa vào các công thức liên quan để tính giá trị các phần tử điện chứa trong hộp kín.

7.2. Bài tập về xác định các phần tử điện chứa trong hộp đen: Bài 1

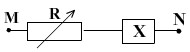
Cho mạch điện như hình vẽ. Điện áp giữa hai đầu đoạn mạch có biểu

thức là

uMN

 200 2 sin100 t

(V). Cường độ

dòng điện i nhanh pha hơn điện áp hai đầu đoạn mạch. X là hộp kín chứa cuộn thuần cảm

hoặc tụ điện. R là biến trở. Điều chỉnh R thấy công suất của mạch cực đại

2

khi I  A. Xác định phần tử điện trong X và giá trị của nó.

Bài 2

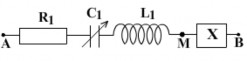
Cho mạch điện như hình vẽ. Tụ điện C1 có điện dung thay đổi được. Điện trở R1 = 100 , cuộn dây thuần cảm có độ tự cảm L1 = 0,318H. Hộp kín X chứa hai

trong ba phần tử điện (thuần Ro, thuần Lo, thuần Co). Đặt vào hai đầu đoạn mạch AB điện áp xoay chiều có U = 200V, f = 50Hz.

­ Khi C1 = 1,59.10­5F thì uMB nhanh pha hơn uAM một góc   5 rad.

12

­ Nếu điều chỉnh C1 để uAM trùng pha với dòng điện thì công suất tiêu thụ của mạch là P = 200W. Hãy xác định các phần tử chứa trong hộp kín X và giá trị của chúng.

Bài 3

2

Cho đoạn mạch AB như hình vẽ. Mỗi hộp X và Y chỉ chứa hai trong ba phần tử: điện trở thuần, cuộn dây thuần cảm và tụ điện mắc nối tiếp. Các

Trang 11

vôn kế

V1, V2 và ampe kế

đo được cả

dòng xoay chiều và một chiều, điện trở các vôn kế rất lớn, điện trở ampe kế không đáng kể.

Khi mắc vào hai điểm A và M hai cực của nguồn điện một chiều, ampe kế chỉ 2A, V1 chỉ 60V.

Khi mắc A và B vào nguồn điện xoay chiều, tần số 50Hz thì ampe kế chỉ

1A, các vôn kế chỉ cùng giá trị 60V nhưng uAM và uMB lệch pha nhau hộp X và Y chứa những phần tử nào? Tính giá trị của chúng.

7.3. Hướng dẫn giải và giải: Bài 1:

Tóm tắt:

 . Hai 2

uMN

 200 2 sin100 t (V)

i nhanh pha hơn u

X chứa tụ điện hoặc cuộn thuần cảm

Pmax khi I 

2 A.

X là gì? Tính giá trị của X.

Các mối liên hệ cần xác lập:

­ X chứa một phần tử điện: tụ điện hoặc cuộn thuần cảm.

­ Cường độ dòng điện i nhanh pha hơn điện áp hai đầu đoạn mạch X chứa tụ điện.

­ Công suất tiêu thụ của mạch:

�  Z 2 �

C

P  I 2 R 

U 2 .R R2  Z 2

 U 2

C

R  Z 2

R

­ Pmax khi �R

C �min. Áp dụng bất đẳng thức Cô­si cho hai số

không

�

âm, ta có:

R �

R  Z 2 �2�R. Z 2 R  Z 2 �2Z

C C C

R R R C

Z 2

Dấu bằng xảy ra khi và chỉ khi

R  C � R  ZC .

R

2

­ Tổng trở của toàn mạch: Z  R2  Z 2  Z  UZC C.

C C I

Tiến trình hướng dẫn học sinh giải:

Hoạt động của giáo viên

Hoạt động của học sinh
­ X là hộp kín chứa tụ điện hoặc cuộn thuần cảm. ­ Theo đề bài, cường độ dòng điện i nhanh pha hơn điện áp hai đầu đoạn

­ X chứa tụ điện. P  I 2 R  U 2 .R  U 2 ­ R2  Z 2 R  Z 2 (*) C C R � Z 2 � ­ Pmax khi �R C �min. � R � Vì R > 0, Z 2  0 . Áp dụng bất đẳng C R thức Cô­si cho hai số không âm, ta có: R  Z 2 2 R. Z 2 C C R R � R  Z 2 �2Z C R C �  Z 2 � �R C �min (dấu = xảy ra) khi và � R � chỉ khi: R  Z 2 � R  Z C R C ­ Z  R2  Z 2  Z 2 (1) C C ­ Z  U (2) I
	chứa phần tử điện nào?
	­ Biểu thức tính công suất tiêu thụ
	của toàn mạch.
	­ Từ biểu thức (*), hãy tìm điều
	kiện để công suất tiêu thụ P đạt giá
	trị cực đại Pmax.
	­ Vậy điều kiện để Pmax là R = ZC.
	­ Biểu thức tính tổng trở Z của đoạn
	mạch gồm R nối tiếp tụ điện C.
	­ Biểu thức tính tổng trở của toàn
	mạch theo định luật Ohm.
	­ Từ (1) và (2) ZC C.