BÀI TẬP CHƯƠNG 2
Bài 2.1.
Nguồn sáng đơn sắc ( 0,6m ) chiếu vào màn phẳng E có hai khe hẹp
S1 và S2 song song và cách nhau d=1mm và cách đều nguồn sáng. Đặt màn M phẳng song song và cách màn E là D=103mm. Khoảng cách giữa hai màn E và M là không khí (no=1).
a. Tính độ rộng khoảng vân trên màn M và vị trí vân sáng thứ hai.
b. Nếu đổ đầy vào khoảng giữa hai màn E và M một chất lỏng trong suốt có chiết suất n thì thấy độ rộng khoảng vân là 0,45 mm. Tính chiết suất n của chất lỏng.
Bài 2.2.
Hai khe Young cách nhau một khoảng l=1mm, đươc
Có thể bạn quan tâm!
-
Gương Fresnel Hình 2.10. Lưỡng Thấu Kính Bile -
Giao Thoa Gây Bởi Bản Mỏng Có Bề Dày Không Đổi. Vân Cùng Độ Nghiêng -
Hai Tia Phản Xạ Từ Cùng Một Tia Tới Tại Mặt Trên Và Mặt Dưới Của Bản Mỏng Không Khí Cho Hệ Thống Vân Tròn Newton -
Tổng Hợp Dao Động Bằng Phương Pháp Giản Đồ Vectơ -
Vị Trí Các Cực Đại, Cực Tiểu Trong Nhiễu Xạ Qua Nhiều Khe -
D Sin K , D Là Khoa ̉ Ng Cách Giư ̃ A Hai Nút Man
Xem toàn bộ 258 trang tài liệu này.
chiếu bằng ánh
sáng đơn sắc bước sóng λ=0,5μm. Màn quan sát đươc
đ ặt cách mặt phẳng
chứ a hai khe một đoan
D = 2m.
a. Tìm khoảng vân giao thoa.
b. Đặt trước m ột trong hai khe một bản mỏng song song , trong suốt, bề dày e=12μm, hệ vân giao thoa trên màn quan sát dic̣ h m ột khoảng 6mm. Tìm chiết suất của bản mỏng.
Bài 2.3.
Một khe sáng hẹp đơn sắc S1 ở phía trên một gương phẳng G (có kích thước nhỏ), cách gương d=0,5mm. Đặt màn phẳng P vuông góc với mặt gương, song song với khe S1 và cách khe là D=3m. Trên màn P thu được những vân sáng, vân tối đều đặn, sắp xếp xen kẽ và tại điểm O là vân tối. Khoảng cách giữa 21 vân sáng liên tiếp là h=36mm.
a. Thiết lập công thức xác định vị trí vân sáng, vân tối trên màn P.
b. Tính độ rộng một khoảng vân và bước sóng ánh sáng nguồn S1.
Bài 2.4.
Chiếu chùm ánh sáng đơn sắc song song, xiên góc 600 so với mặt
trên của một nêm thủy tinh, đặt trong không khí. Chiết suất của nêm là n=1,5. Góc nghiêng của nêm là rất nhỏ. Bước sóng ánh sáng là .
a. Viết công thức xác định vị trí vân sáng, vân tối của hệ vân giao thoa ở trên mặt nêm theo bề dày của nêm.
b. Đồng thời chiếu hai chùm sáng song song đỏ và tím xiên góc 600
so với mặt nêm. Bước sóng t
0, 4m, d
0, 76m, 2.104 rad . Tìm bề
dày nhỏ nhất của nêm mà tại đó có vân sáng màu đỏ, vân sáng màu tím.
Bài 2.5.
Giữa hai bản thủy tinh phẳng (n1=1,5) đặt nghiêng với nhau một góc rất nhỏ, đổ đầy nước trong suốt (n=4/3), tạo thành một nêm nước. Chiếu chùm sáng đơn sắc song song tới nêm theo phương vuông góc mặt dưới nêm. Quan sát thấy ở mặt trên của nêm những vân sáng tối xen kẽ đều đặn.
a. Thiết lập công thức xác định vị trí các vân sáng, vân tối.
b. Chiếu đồng thời hai chùm sáng song song đỏ và tím vuông góc với mặt dưới của nêm. Tính khoảng cách giữa vân đỏ bậc hai và vân tím bậc hai ở trên mặt nêm. Biết bước sóng ánh sáng đỏ và ánh sáng tìm lần lượt là:
t 0, 4m, d
0, 76m, và 5.104 rad .
Bài 2.6.
Chiếu chùm sáng đơn sắc song song ( 0,6m ) vuông góc với một bản mỏng (n=1,5) đặt trong không khí. Quan sát thấy trên mặt bản mỏng có những vệt sáng, vệt tối xen kẽ.
a. Giải thích hiện tượng và thiết lập công thức xác định bề dày bản mỏng ứng với vệt sáng, vệt tối.
b. Tìm bề dày nhỏ nhất của bản mỏng mà tại đó có vệt tối, có vệt sáng.
Bài 2.7.
Một chùm ánh sáng đơn sắc song song có bước sóng λ=0,5μm chiếu vuông góc với một mặt của nêm không khí . Quan sát trong ánh sáng phản xa ,̣ người ta đo được độ rộng của mỗi vân giao thoa bằng i=0,5mm.
a. Xác điṇ h góc nghiêng của nêm.
b. Chiếu đồng thời vào mặt nêm không khí hai chùm tia sáng đơn sắ c có bước sóng lần lượt là λ1=0,5μm, λ2=0,6μm. Tìm vi ̣trí taị đó các vân tối cho bởi hai chùm sáng nói trên trùng nhau . Coi caṇ h của bản mỏng nêm không khí là vân tối bậc không.
Bài 2.8.
Một bản mỏng nêm thuỷ tinh có góc n ghiêng α =2′ và chiết suất n=1,52. Chiếu một chùm sáng đơn sắc song song vuông góc với một mặt của bản. Xác điṇ h bước sóng của chùm sáng đơn sắc nếu khoảng cách giữa h ai vân tối kế tiếp bằng i=0,3mm.
Bài 2.9.
Hai tia sáng đơn sắc song song chiếu vào mặt trên của bản mỏng có bề
2
o
dày d không đổi, chiết suất n1 với góc tới i1=45 . Phía trên bản mỏng là
không khí (no=1), phía dưới là thủy tinh (n2=1,5) bề dày d=0,49µm, bước sóng ánh sáng 0, 6m.
a. Tính hiệu quang lộ của hai tia gặp nhau tại M.
b. Tại M là điểm sáng hay điểm tối.
Bài 2.10.
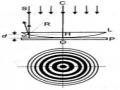
Chiếu một chùm sáng đơn sắc song song vuông góc với bản thủy tinh phẳng của dụng cụ cho vân giao thoa tròn Newton. Quan sát thấy bán kính của hai vân tối liên tiếp lần lượt bằng 4,38mm và 4,73mm. Bán kính của chỏm cầu R=6,4m. Chiết suất thủy tinh của dụng cụ là n=1,5.
a. Giải thích sự tạo thành hệ vân giao thoa tròn Newton. Hãy cho biết số thứ tự của hai vân tối nói trên và tính bước sóng của ánh sáng.
b. Nếu đổ đầy nước trong suốt (n1=4/3) vào khe giữa chỏm cầu và tấm thủy tinh phẳng của dụng cụ thì hệ vân giao thoa thay đổi như thế nào?
Bài 2.11.
Một dụng cụ cho vân tròn Newton gồm một thấu kính mỏng bằng thủy
tinh (n2=1,5) có dạng phẳng – lòm, bán kính mặt lòm R=2m được đặt sao cho mặt lòm hướng lên trên và được đổ đầy nước trong suốt (n1=4/3). Chiếu chùm tia sáng đơn sắc song song (bước sóng 0, 65m) vuông góc với mặt nước. Xác định bề dày của lớp thủy tinh tại vị trí vân tối thứ 10 và tính bán kính vân tối đó.
Bài 2.12.
Dụng cụ giao thoa cho hệ vân tròn Newton gồm chỏm cầu bằng thủy tinh phẳng nằm ngang, (có cùng chiết suất n=1,5). Bán kính chỏm cầu R=8,6m. Chiếu một chùm sáng song song, đơn sắc vuông góc với mặt bản thủy tinh. Quan sát thấy hệ vân tròn giao thoa Newton, đường kính vân tối thứ tư là 9mm. Coi tâm hệ vân là vân tối thứ không. Khe giữa chỏm cầu và tấm thủy tinh là không khí (no=1).
a. Tính bước sóng của ánh sáng tới dụng cụ giao thoa.
b. Nếu đổ chất lỏng (n1=1,4) và đầy khe giữa chỏm cầu và tấm thủy tinh thì hệ vân giao thoa thay đổi như thế nào?
Bài 2.13.
Hai bản thủy tinh phẳng (n=1,5) đặt nghiêng với nhau một góc α rất nhỏ, tạo thành một nêm không khí giữa khe. Chiếu một chùm sáng đơn sắc
0,6m vuông góc mặt dưới của nêm không khí. Quan sát thấy hệ vân giao thoa trên mặt nêm và trên 1cm dài của mặt nêm thấy có 11 vân tối.
a. Tính góc nghiêng của nêm.
b. Đổ đầy chất lỏng trong suốt có chiết suất n1=1,4 vào đầy khe nói trên thì hệ vân thay đổi như thế nào?
Bài 2.14.
Chiếu một chùm ánh sáng trắng vào một màng xà phòng (coi là bản mỏng có bề dày thay đổi, chiết suất n=1,33). Tìm bề dày nhỏ nhất của màng xà phòng mà tại đó có những tia phản chiếu màu vàng. Xét hai trường hợp:
a. Góc tới là 45o.
b. Chùm tia tới vuông góc với màng xà phòng.
Cho biết bước sóng ánh sáng vàng
Bài 2.15.
0,6m .
Xét một hệ thống cho vân tròn Newton . Xác điṇ h bề dày củ a lớp không khí ở đó ta quan sát thấy vân sáng đầu tiên , biết rằng á nh sáng tới c ó bước sóng λ=0,6μm.
Bài 2.16.
Cho một chùm sáng đơ n sắc song song bước sóng λ=0,6μm, chiếu vuông góc với mặt phẳng của bản mỏng không khí nằm giữa bản thuỷ tinh phẳng đặt tiếp xúc với m ặt cong của m ột thấu kính phẳng - lồi. Tìm bề dày của lớp không khí taị vi ̣trí vân tối thứ tư của chùm tia phản xa ̣ . Coi tâm của h ệ vân tròn Newton là vân số 0.
Bài 2.17.
Cho một chùm sáng đơn sắc song song chiếu vuông góc với m ặt phẳng của bản mỏng không khí nằm giữa bả n thuỷ tinh phẳng đ ặt tiếp xúc với m ặt cong của m ột thấu kính phẳng - lồi. Bán kính mặt lồi thấu kính là R=15m.
Quan sát hệ vân tròn Newton qua chùm sáng phản xa ̣và đo đươc khoảng cách
giữa vân tối thứ tư và vân tối thứ hai mươ i lă m bằng 9mm. Xác điṇ h bước sóng của chùm sáng đơn sắc. Coi tâm của hệ vân tròn Newton là vân số 0.
Chương 3.NHIỄU XẠ ÁNH SÁNG
3.1. HIỆN TƯỢNG NHIỄU XẠ ÁNH SÁNG. NGUYÊN LÍ HUYGENS- FRESNEL
3.1.1. Hiện tượng nhiễu xạ ánh sáng
Trong quang hình học ở môi trường đồng tính, ánh sáng sẽ truyền thẳng. Tuy nhiên thực nghiệm chứng tỏ rằng điều đó không phải bao giờ cũng đúng. Xét hai thí nghiệm sau đây:
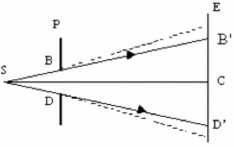
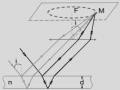
Thí nghiệm 1:Dùng đèn pin S rọi vào một lỗ tròn đường kính BD trên một tấm bìa dày P (Hình 3.1). Theo định luật truyền thẳng của ánh sáng thì ta chỉ quan sát được ánh sáng trong hình nón SB'D' do các tia sáng đi qua mép lỗ tròn tạo nên. Tuy nhiên nếu ta đặt mắt
tại điểm M ở ngoài và ngay cả khá xa hình nón này vẫn nhận được ánh sáng từ S.
Hình 3.1
Điều đó chứng tỏ ánh sáng truyền cả vào miền bóng tối hình học, tức là không tuân theo định luật truyền thẳng của ánh sáng.
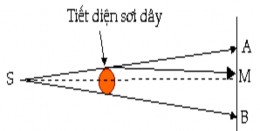
Thí nghiệm 2:Ðặt một miếng bìa dày, hình tròn O song song với một khe sáng. Sau miếng bìa ta đặt một màn quan sát E (Hình 3.2) song song với O. Theo định luật truyền thẳng thì miền AB bị che
khuất bởi sợi dây phải là miền bóng tối hình học và ngoài miền đó phải được rọi sáng đều. Tuy nhiên tại điểm M nằm trên
Hình 3.2
trục đối xứng của AB ở trong miền bóng tối hình học, ta vẫn thấy có ánh sáng
và ở lân cận các điểm A và B ta lại thấy các vân tối và sáng.
Ðiều đó cho thấy rằng, trong trường hợp này ánh sáng cũng không tuân theo định luật truyền thẳng.
Trong cả hai thí nghiệm nói trên, màn chắn có lỗ BD và miếng bìa chắn sáng O là các vật cản đóng vai trò phân bố lại cường độ sáng trên màn quan sát.
Hiện tượng quan sát được ở hai thí nghiệm đó là những thí dụ về hiện tượng nhiễu xạ ánh sáng.
Điṇ h nghiã
Hiện tương tia sáng bi ̣l ệch khỏi phươ ng truyền thẳng khi đi gần các
chướng ngai
vật có kích thướ c nhỏ đươc
goi
là hiện tươn
g nhiêu
xạ ánh sáng.
Hiện tươn
g nhiêu
xa ̣ánh sáng có
thể giải thích đư ợc một cách định tính
dưa
vào nguyên lí Huygens.
Tuy nhiên nguyên lí Huygens
chưa cho biết cường độ sáng trên màn đặt sau vật cản sẽ được phân bố như thế nào. Ðể giải quyết vấn đề này Fresnel
Hình 3.3
bổ sung nguyên lí giao thoa vào nguyên lí Huygens và lập nên nguyên lí Huygens-Fresnel. Ðó là nguyên lí cơ bản của quang học sóng.
3.1.2. Nguyên lí Huygens-Fresnel
a. Phát biểu
Môi
điểm trong không gian đươc
sóng ánh sáng từ nguồn thưc
gử i đến
đều trở thành nguồn sáng thứ cấp phát sóng ánh sáng về phía trước.
Biên độ và pha của nguồn thứ cấp là biên đ ộ và pha do nguồn thưc
gây ra tai
vi ̣trí của nguồn thứ cấp.
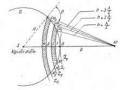
Theo nguyên lí Huygens –Fresnel, khi ánh sáng chiếu đến lỗ tròn , các điểm trên lỗ tròn đều trở thành nguồn thứ cấp phát sóng cầu thứ cấp . Bao hình của các m ặt sóng cầu thứ cấp là m ặt sóng . Ở mép của lỗ tròn m ặt sóng bị uốn cong và tia sóng
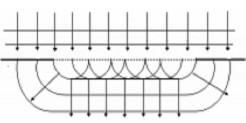
Hình 3.4. Giải thích định tính hiện tượng nhiễu xạ ánh sáng
luôn vuông góc với mặt sóng, do đó ở mép biên các tia sóng bi ̣đổi phương so với phương của sóng tới (Hình 3.4).
Mỗi nguồn sáng thứ cấp trên m ặt lỗ tròn BD có biên độ và pha dao động đúng bằng biên đ ộ và pha dao động do nguồn sáng S gây ra taị điểm đó . Dao động sáng taị mỗi điểm trên màn ảnh E sẽ bằng tổng các dao đ ộng sáng do những nguồn sáng thứ cấp trên lỗ tròn BD gây ra taị điểm đó . Từ biểu thứ c
của hàm sóng , dưạ
biểu thứ c điṇ h lươn
vào nguyên lí Huyge ns-Fresnel người ta có thể tìm đươc̣
g của dao đ ộng sáng taị m ột điểm M trên màn hình E ,
nhưng vi ệc tính toán khá phứ c tap vì phải tính tích phân . Fresnel đã đưa ra
một phương pháp tính đơn giản goi là phương pháp đới cầu Fresnel mà chúng
ta sẽ được tìm hiểu trong phần tiếp theo.
3.1.2.2. Biểu thức sóng Bài toán:
Cho dao động sáng tại nguồn O có dạng x acost , hãy tìm biểu thức
xác định dao động sáng tại M.
Ta áp dụng nguyên lí Huygens-Fresnel để viết biểu thức dao động sáng gây ra tại M.
Có thể thay nguồn sáng điểm O bằng một mặt kín phát sáng S bao quanh O. Theo nguyên lí Huygens, mỗi điểm dS trên mặt S
đều nhận được ánh sáng do O gửi tới nên dS
được xem là các nguồn ảo phát sóng cầu thứ
Hình 3.5
cấp, chúng là sóng kết hợp, do đó có thể giao thoa với nhau.
Như vậy để tìm biểu thức sóng tại M bên ngoài mặt S ta không cần chú ý tới O mà chỉ cần dùng các nguồn thứ cấp dS phân bố trên mặt S.
Theo nguyên lí Fresnel, dao động sáng tại dS do O gửi tới có dạng:
dx(dS) a(dS)cos(t r1 )
v
trong đó a(dS) ~ a
r1
là biên độ dao động sáng do nguồn O gây ra tại dS.