Hai Tia Phản Xạ Từ Cùng Một Tia Tới Tại Mặt Trên Và Mặt Dưới Của Bản Mỏng Không Khí Cho Hệ Thống Vân Tròn Newton

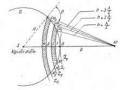
Tia 1: SIML, đi từ S, tới I, truyền qua G1, phản xạ tại M (mặt dưới của bản thủy tinh G1), truyền qua G1 tới L.

tq G1

(1) S I 

phanxa

M

tq G1

L

Tia 2: SIMKMI, đi từ S, tới I, truyền qua G1, truyền qua lớp không khí tới K, phản xạ tại K (mặt dưới của bản thủy tinh G2), quay lại M, truyền qua G1 quay lại I.

Có thể bạn quan tâm!

• Các Đại Lượng Trắc Quang Là Các Đại Lượng Dùng Trong Kĩ Thuật Đo Lường Ánh Sáng.
• Gương Fresnel Hình 2.10. Lưỡng Thấu Kính Bile
• Giao Thoa Gây Bởi Bản Mỏng Có Bề Dày Không Đổi. Vân Cùng Độ Nghiêng
• Hiện Tượng Nhiễu Xạ Ánh Sáng. Nguyên Lí Huygens- Fresnel
• Tổng Hợp Dao Động Bằng Phương Pháp Giản Đồ Vectơ
• Vị Trí Các Cực Đại, Cực Tiểu Trong Nhiễu Xạ Qua Nhiều Khe

Xem toàn bộ 258 trang tài liệu này.

tq G1

kk phanxa kk

tq G1

(2) S I M 

K

2

M I

Tại M có sự gặp nhau của hai tia phản xa ̣nói trên và chúng giao thoa với

nhau. Trên mặt G1 ta nhận đươc

Tính hiệu quang lộ

vân giao thoa.

Xét hai tia sáng phản xạ tại M và tại K, chỉ có tia sáng phản xạ tại K là phản xạ trên môi trường (thủy tinh) có chiết suất lớn hơn môi trường ánh sáng

tới (không khí). Do vậy, quang lộ của đường truyền tia 2 được cộng thêm .

2

Còn tia 1 phản xạ trên m ặt dưới của G1 thì không thay đổi quang l ộ vì đây là phản xa ̣tr ên môi trường không khí , kém chiết quang hơn môi trường ánh sáng tới (thủy tinh) (Hình 2.18).

Vậy, hai tia giao thoa tại M có quang lộ là:

L1 SI n.IM

L SI n.IM MK KM

22

Chú ý, ở đây ta chỉ tìm quang lộ của hai tia sáng truyền từ nguồn S đến điểm giao thoa M.

L L  2MK  2d 

(2.14)

2 1 2 2

với d là bề dày của lớp không khí taị M.

Vị trí và hình dạng của vân giao thoa

Các điểm tối thoả mãn điều kiện:

L L  (k 1 ) 2d 

2 1 2 2

d k , với k=0,1,2, ... (2.15)

2

Do tập hơp các điêm̉ có cùng bề dày d của lớp không khí là m ột đoan

thẳng song song với caṇ h nêm nên các vân tối là các đoạn thẳng song song với cạnh nêm. Tại cạnh nêm d =0, ta có một vân tối.

Các điểm sáng thoả mãn điều kiện:

L2 L1

k 2d 

2

d  (2k 1) , k=1,2,3, ... (2.16)

4

Vậy các vân sáng cũng là những đoan nằm xen kẽ với vân tối.

Bài toán 2:

thẳng song song với caṇ h nêm và

Một chùm sáng song song có bước

 0, 6m

chiếu vuông góc với mặt

nêm không khí. Tìm góc nghiêng của nêm. Cho biết độ rộng của 10 khoảng vân kế tiếp ở mặt trên của nêm bằng b  10mm.

Giải:

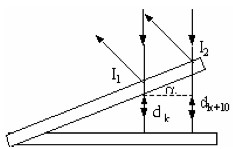
Hiệu quang lộ hai tia:

L  2d  (2k 1) 

2 2

Độ dày của nêm không khí tại vị trí vân tối thứ k :

d k, k  0,1, 2, 3....

k2

Độ dày của nêm không khí tại vị trí vân tối thứ k 10 :

dk 10

(k 10)

2

 sindk 10 dk

(k 10) k 

 2 2

5 3.104 rad.

I1I2 b b

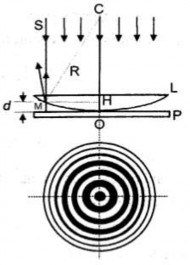
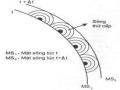
2.3.2.3. Vân tròn Newton

Hệ cho vân tròn Newton gồm m ột thấu kính phẳng - lồi đ ặt tiếp xúc với m ột bản thủy tinh phẳng (Hình 2.19). Lớp không khí giữa thấu kính và bản thủy tinh là bản mỏng có bề dày thay đổi.

a. Hiện tượng

Chiếu một chùm tia sáng đơn sắc song song vuông góc với bản thủy tinh c ủa hệ cho vân tròn Newton. Tại mặt cong của thấu kính, ta thấy xuất

hiện các vân sáng, tối là các vòng tròn đồng tâm nằm xen kẽ nhau, tại tâm là một vân tối.

b. Giải thích

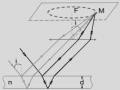
Đường truyền tia sáng

Hình 2.19. Vân tròn Newton

Tương tự như nêm không khí, ta xét sự giao thoa của hai tia sáng kết hợp tách ra từ chùm sáng song song, phản xạ tại mặt dưới của thấu kính và mặt trên của bản thủy tinh phẳng, và giao thoa tại mặt cong của thấu kính M (Hình 2.19, 2.20).

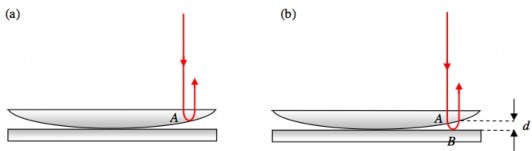
Hình 2.20. Hai tia phản xạ từ cùng một tia tới tại mặt trên và mặt dưới của bản mỏng không khí cho hệ thống vân tròn Newton

Vị trí và hình dạng của vân giao thoa

Giống như nêm không khí, vân tối ứng với bề dày của lớp không khí:

d k 

2

Vân sáng ứng với bề dày của lớp không khí:

d  (2k 1) 

4

Do tính chất đối xứ ng của bản mỏng nên các vân giao thoa là những

vòng tròn đồng tâm goi là vân tròn Newton.

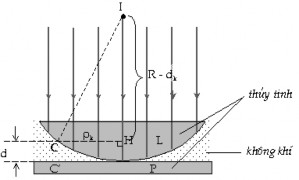
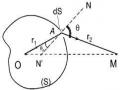
Tính bán kính của vân thứ k

Xét tam giác vuông CHI, ta có:

CI 2 HC2 IH 2

R2 2  (R d )2

k k

2  2Rd d2

k k k

trong đó: R là bán kính cong của

thấu kính, dk

là bề dày của lớp

Hình 2.21. Tính bán kính vân tròn Newton

không khí tại vân tối thứ k.

Vì dk R, do đó:

k

k

2  2Rd

Tại vân tối thứ k, ta có dk

Rk

k 

k , do đó:

2

(2.17)

Như vậy, bán kính của các vân tối tỉ lệ với căn bậc hai của các số nguyên liên tiếp.

Bài toán 3:

Một chùm sáng đơn sắc song song chiếu vuông góc với mặt phẳng của bản mỏng không khí nằm giữa bản thủy tinh phẳng đặt tiếp xúc với mặt cong của thấu kính thẳng – lồi. Bán kính của mặt lồi thấu kính là R  6, 4m. Quan sát hệ vân tròn Newtron trong chùm sáng phản xạ, người ta đo được bán kính của hai vân tối kế tiếp lần lượt là 4, 0mm và 4, 38mm.

Xác định bước sóng của chùm sáng chiếu tới.

Giải:

Bán kính của hai vân tối kế tiếp thứ k và được xác định bởi công thức:

k 1 trong hệ vân tròn Newton

(k 1)R

rk kR, rk 1 

r2 r2

k k, k 1 k1

RR

r2 r2

k1k 1

RR

Vậy, bước sóng chùm ánh sáng chiếu tới:

2

k1 k

r

r2  (4, 38.103 )2  (4.103 )2 6

0, 497.10

m

R 6, 4

TỔNG KẾT CHƯƠNG 2

1. Giao thoa ánh sáng

a. Định nghĩa

Hiện tươn

g giao thoa ánh sáng là hi ện tươn

g g ặp nhau của hai hay

nhiều sóng ánh sáng kết hơp

, kết quả là trong trườ ng giao thoa s ẽ xuất hi ện

những vân sáng và những vân tối xen kẽ nhau.

b. Điều kiện giao thoa

Hiện tươn

g giao thoa chỉ xảy ra đối vớ i sóng ánh sáng kết hơp

. Sóng

ánh sáng kết hơp

là những sóng có hiệu pha không thay đổi theo thờ i gian.

c. Điều kiện cưc

đai

giao thoa

L1 L2 k , với k=0, 1, 2, ..

d. Điều kiện cưc tiêủ giao thoa

2. Giao thoa Young

L1 L2

 (k 1 ) , với k=0, 1, 2, ..

2

a. Vị trí các vân sáng (cưc

đai

giao thoa)

x k D, k  0, 1, 2...,

a

b. Vị trí các vân tố i (cưc tiêủ giao thoa)

x  (k 1 ) D , k  0, 1, 2...

2 a

c. Khoảng cách giữa hai vân sáng (hoặc vân tố i) kế tiếp

i D

a

3. Giao thoa gây bởi bản mỏng

a. Giao thoa do phản xa ̣

Khi phản xạ trên môi trườ n g chiết quang hơ n môi trườ ng ánh sáng tớ i ,

quang lộ của tia phản xạ dài thêm một đoan λ/2.

b. Giao thoa của nêm không khí

Nêm không khí là một lớ p không khí hình nêm giớ i han

bởi hai bản thuy

tinh phẳng G 1, G2 có độ dày không đáng kể , đặt nghiêng vớ i nhau m ột góc nhỏ α. Do sự giao thoa của các tia phản xạ ở mặt trên và mặt dưới của nêm,

ta thu đươc

các vân thoa ở ngay m ặt trên củ a nêm . Cưc

tiểu vân giao thoa

nằm tai

vi ̣trí ứ ng vớ i bề dày của lớ p không khí:

d k 

2

với k=0,1,2, ...

Tập hơp

các điểm có cùng bề dày d của lớ p không khí là m ột đoan

thẳng

song song vớ i can

h nêm. Tại cạnh nêm d = 0 ta có một vân tối.

Cưc

đai

vân giao thoa nằm tai

vi ̣trí ứ ng vớ i bề dày lớp không khí:

d  (2k 1) 

4

với k=1,2,3 ..

Vân sáng cũng là những đoan kẽ với vân tối.

c. Vân tròn Newton

thẳng song song vớ i can

h nêm và nằm xen

Hệ cho vân tròn Newton gồm m ột thấu kính phẳng - lồi đặt tiếp xúc vớ i một bản thủy tinh phẳng . Lớ p không khí giữa thấu kính và bản thủy tinh là bản mỏng có bề dày thay đổi.

Giống như nêm không khí , cưc bề dày của lớ p không khí:

tiểu vân giao thoa nằm tai

vi ̣trí ứ ng vớ i

d k 

2

với k=0,1,2, ...

và cưc

đai

vân giao thoa nằm taị

d  (2k 1) 

4

vi ̣trí ứ ng vớ i bề dày lớ p không khí:

với k=1,2,3 ..

Do tính chất đối xứ ng của bản mỏng nên các vân giao thoa là những

vòng tròn đồng tâm goi là vân tròn Newton.

Bán kính của vân tối thứ k:

Rk

k 

CÂU HỎ I LÝ THUYẾ T

1. Nêu điṇ h nghia

hi ện tươn

g giao thoa ánh sáng , điều ki ện giao thoa ánh

sáng. Thế nào là sóng ánh sáng kết hơp ?

2. Tìm điều kiện cưc

đaị , cưc

tiểu giao thoa. Xác điṇ h vi ̣trí các vân giao thoa

cưc

đaị và cưc

tiểu, bề rộng của các vân giao thoa.

3. Mô tả hiện tươn

g giao thoa khi dùng ánh sáng trắng.

4. Trình bày hiện tượng giao thoa gây bởi bản mỏng có bề dày không đổi. Tại sao vân giao thoa trong trường hợp này gọi là vân cùng độ nghiêng?

5. Trình bày hiện tượng giao thoa gây bởi bản mỏng có bề dày thay đổi. Tại sao vân giao thoa trong trường hợp này gọi là vân cùng độ dày?

6. Trình bày hiện tươn

7. Trình bày hiện tươn

g giao thoa gây bởi nêm không khí.

g giao thoa cho bởi hệ vân tròn Newton.