Nếu số khe hep
N = 3 (số lẻ) thì các dao động sáng do hai khe
hẹp gửi tới sẽ khử nha u, còn dao động sáng do khe thứ ba gây ra
không bi ̣khử . Kết quả là giữa hai cưc
đaị chính là m ột cưc
đaị .
Cưc
đaị này có cường đ ộ khá nhỏ , nên đươc
goi
là cưc
Có thể bạn quan tâm!
-
Hiện Tượng Nhiễu Xạ Ánh Sáng. Nguyên Lí Huygens- Fresnel -
Tổng Hợp Dao Động Bằng Phương Pháp Giản Đồ Vectơ -
Vị Trí Các Cực Đại, Cực Tiểu Trong Nhiễu Xạ Qua Nhiều Khe -
Đu ̛ Ơ ̀ Ng Đ Ặc Tru ̛ Ng Phổ Phát Xạ Cu ̉ A Vật Đen Tuyệt Đối -
Vật lý đại cương 2 - 31 -
Vật lý đại cương 2 - 32
Xem toàn bộ 258 trang tài liệu này.
đai
phu ̣.
Rò ràng giữa cưc
đaị phu ̣này và hai cưc
đaị chính hai bên phải
có hai cưc tiêủ phu.
Người ta chứng minh được rằng , nếu cách tử có N khe hep thì giữa hai
cưc
đaị chính sẽ có N-1 cưc
tiểu phu ̣ và N-2 cưc
đaị phu.
Hình 3.24 biểu diên
ảnh nhiễu xạ qua ba khe hẹp và chỉ rò vị trí các cực đại, cực tiểu. Nếu N lớn thì bề rộng các cực đại chính hẹp, và cực đại chính quan sát được sẽ thanh nét. Vì các cực đại phụ kém sáng hơn rất nhiều so với các cực đại chính nên ta không cần chú ý đến chúng và ảnh nhiễu xạ qua nhiều khe hẹp sẽ là một dãy các vạch sáng song song, cách đều nhau. Từ công thức () ta thấy: muốn quan sát được các cực đại chính thì d (vì sin1).
3.4.3. Cách tử nhiễu xạ
a. Khái niệm
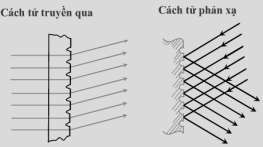
Cách tử nhiễu xạ là một hệ nhiều khe hẹp giống nhau có đ ộ rộng b, nằm song song cách đều trên cùng m ột mặt phẳng . Khoảng cách d giữa hai khe kế tiếp đươc̣ gọi là chu kì của cách tử.
b. Phân loại
Có hai loại cách tử nhiễu xạ là: cách tử phản xạ và cách tử truyền qua.
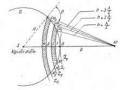
3.4.4. Nhiễu xạ trên tinh thể
Các nguyên tử (phân tử hay ion ) cấu tao
Hình 3.25. Cách tử nhiễu xạ
Hình 3.26.
nên v ật rắn tinh thể đươc
sắp
xếp theo m ột cấu trúc tuần hoàn goi
là maṇ g tinh thể , trong đó vi ̣trí của các
nguyên tử (phân tử hay ion) gọi là nút mạng. Khoảng cách giữa các nút mạng,
đặc trưng cho tính tuần hoàn , đươc
goi
là chu kì của maṇ g tinh thể . Chiếu lên
tinh thể m ột chùm tia Rơnghen , mỗi nút maṇ g trở thành tâm nhiêu
xa ̣và
mạng tinh thể đóng vai trò như một cách tử với chu kì là chu kì của maṇ g tinh
thể. Chùm tia Rơnghen sẽ nhiêu xạ theo nhiều phương , tuy nhiên chỉ theo
phương phản xạ gương (phương mà góc phản xạ bằng góc tới), cường độ của
tia nhiêu
xa ̣đủ lớn để ta có thể quan sát đươc
ảnh nhiêu
xa.̣
Xét các tia nhiễu xạ theo phương phản xạ gương. Hiệu quang lộ giữa hai tia phản xạ trên hai mặt phẳng 11' và 22' là:
2d sin(3.24)
Hiệu quang lộ giữa hai tia phản xạ trên hai mặt phẳng 11' và 33' là 2. Như vậy theo phương phản xạ gương, sẽ có
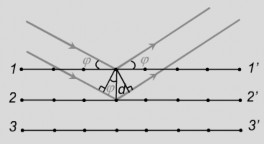
Hình 3.27. Nhiễu xạ trên tinh
một chùm tia nhiễu xạ với hiệu quang lộ là , 2, 3, ..., các tia nhiêu
xa ̣này
sẽ giao thoa với nhau và cho cực đại nhiễu xạ nếu hai tia nhiễu xạ kế tiếp có hiệu quang lộ bằng số nguyên lần bước sóng:
2d sink
hay:
sink , (3.25)
2d
với d là khoảng cách giữa hai m ặt phẳng nguyên tử của v ật rắn tinh thể (chu kì maṇ g tinh thể). Công thứ c (3.25) gọi là công thức Vulf -Bragg. Đây là công thứ c cơ bản để phân tích cấu trúc của v ật rắn tinh thể bằng tia Rơnghen . Nếu
biết bước sóng của tia Rơnghen và đo góc ta có thể xác điṇ h đươc
d nghĩa là xác định được cấu trúc của mạng tinh thể.
chu kì
1. Hiện tư ơn
g nhiêu
TỔNG KẾT CHƯƠNG 3
xa ̣ ánh sáng
Hiện tương tia sáng bi ̣l ệch khỏi phươ ng truyền thẳng khi đi gần các
chướng ngại vật có kích thướ c nhỏ đươc
2. Nguyên lí Huygens - Fresnel:
a. Phát biểu
goi
là hiện tươn
g nhiêu
xạ ánh sáng.
Môi
điểm trong không gian đươc
sóng ánh sáng từ nguồn thưc
gử i đến
đều trở thành nguồn sáng thứ cấp phát sóng ánh sáng về phía trướ c.
Biên độ và pha của nguồn thứ cấp là biên đ ộ và pha do nguồn thưc̣
gây
ra tai
vi ̣trí của nguồn thứ cấp.
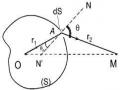
b. Biểu thức sóng tổng hợp tại M
x dx(M ) A(,0) cos(t r1r2)dS
(S )
3. Phương pháp đới cầu Fresnel
r1r2v
Biên độ tổng hợp do các đới cầu Fresnel gây ra tại M là:
a a1 a2 a3 a4 a5 a6...
4. Nhiêu xa ̣ sóng cầu qua lỗ tròn
Áp dun
g phươ ng pháp đớ i cầu Fresnel , ta tính đươc
biên đ ộ của ánh
sáng tổng hơp
tai
M, cách nguồn S một khoảng R:
a a1 an ,
2 2
dấu "+" ứng với n lẻ, dấu "-" ứng với n chẵn.
Xét các trường hợp:
Khi không có màn chắn P ho ặc kích thướ c lỗ tròn rất lớ n : n , an 0
nên cườ ng độ sáng tai M:
2 a2
I0 ka
k1.
4
Nếu lỗ chứ a số lẻ đớ i cầu:
I ka2 k( a1 an )2 I ,
2 2 0
điểm M sáng hơn khi không có màn P.
Đặc biệt, nếu lỗ chứ a m ột đớ i cầu : n 1 a a1
1
0
I ka2 4I .
Cường độ sáng gấp 4 lần so vớ i khi không có lỗ tròn , như vậy điểm M rất sáng.
Nếu lỗ chứ a số chẵn đớ i cầu:
I ka2 k( a1 an )2 I ,
2 2 0
điểm M tối hơ n khi không có lỗ tròn.
Đặc biệt, nếu lỗ tròn chứ a hai đớ i cầu thì : a a1 a2
0 I 0,
2 2
điểm M tối hoàn toàn.
Tóm lai
điểm M có thể sáng hơ n hoặc tối hơ n so vớ i khi không có lỗ tròn
tuỳ theo kích thước của lỗ và vị trí của màn quan sát.
5. Nhiêu xa ̣ sóng cầu qua đĩa tròn
Biên độ dao động sáng tại M là:
a am1 am2 am3 am4 am5 ...
a am1
2
I ka2 k( am1 )2 k( a1 )2 I .
2 2 0
Như vậy:Nếu đĩa chỉ che mất một ít đới, thì tại M ta luôn có một điểm sáng có cường độ sáng nhỏ hơn một chút so với cường độ sáng tại M trong trường hợp không có vật chắn sáng.
6. Nhiêu
xa ̣ của sóng phẳng qua một khe hep
Áp dun
g phươ ng pháp đớ i cầu Fresnel ta tính toán đươc
biên đ ộ dao
động sáng tổng hơp
tai
một điểm M trên màn quan sát.
Kết quả ta có các điều ki ện cưc như sau:
đaị , cưc
tiểu n hiêu
xạ qua m ột khe hep
Cưc
đai
giữa:
sin 0
Cưc
tiểu nhiêu
xa:
sin; 2 ;
b b
3
b
; ...
Cưc
đai
nhiêu
xa:
sin3; 5; 7 ; ...
2b 2b 2b
Trên đồ thi ̣phân bố cườ ng đ ộ sáng ta thấy cưc
đai
giữa rất sán g, các
cưc
đai
nhiêu
xạ b ậc k =1,2,3...nằm xen giữa các cưc
tiểu nhiêu
xạ và
phân bố đối xứ ng ở hai bên cưc
đai
giữa . Cưc
đai
giữa có bề r ộng gấp
đôi các cưc
đai
khác . Theo tính toán lí thuyết , cường đ ộ sáng của các
cưc
đai
nhiêu
xạ tuân theo hệ thứ c sau:
I0 : I1 : I2 : I3 : ... 1: 0, 045 : 0, 016 : 0, 008 : ...
7. Nhiễu xạ trên tinh thể
Đối với v ật rắn tinh thể , mạng tinh thể đóng vai trò m ột cách tử không
gian ba chiều. Sự nhiêu
xạ của các tia X trên các nút man
g cho ta kết quả:
2d sink, d là khoảng cách giữa hai nút man
g , gọi là hằng số mạng . Đây
là công thứ c Vulf-Bragg, đươc dùng để xác điṇ h cấu trúc của vật rắn tinh thể.
CÂU HỎI LÍ THUYẾT
1. Nêu điṇ h nghia
hiện tươn
g nhiêu
xa ̣ánh sáng. Dùng nguyên lí Huygens
giải thích định tính hiện tươn
g nhiêu
xa.
2. Phát biểu nguyên lí Huygens-Fresnel.
3. Trình bày phương pháp đới cầu Fresnel : cách chia đới, tính cường độ sáng và biên độ tổng hợp.
4. Khảo sát hiện tươn
g nhiêu
xa ̣ánh sáng qua lỗ tròn nhỏ và qua một đĩa
tròn, nêu sự khác nhau giữa hai hiện tượng trên.
5. Mô tả hi ện tươn
g nhiêu
xa ̣ánh sáng qua m ột khe hep
. Tìm điều ki ện
cưc
đaị , cưc
tiểu nhiêu
xa ̣ . Vẽ ảnh nhiễu xạ của sóng phẳng qua m ột
khe hep̣ .
6. Khảo sát nhiễu xạ qua N khe của sóng phẳng, định nghĩa cực tiểu chính và phụ, cực đại chính và phụ. Vẽ ảnh nhiễu xạ của sóng phẳng qua ba khe hep̣ , chỉ rò vị trí các cực đại và cực tiểu.
7. Trình bày nhiêu
xa ̣của tia X trên tinh thể . Công thứ c Vulf - Bragg. Nêu
ứng dun
g của hiện tươn
g nhiêu
xa ̣tia X.
BÀI TẬP CHƯƠNG 3
Bài 3.1.
Một nguồn sáng S phát ra ánh sáng đơn sắc có bước sóng là 550nm, chiếu vào màn ảnh E cách S một khoảng 11m. Ở điểm giữa màn E và nguồn S có một màn chắn có chứa một lỗ tròn đường kính 4,2mm. Cho biết độ sáng tại trung tâm của hình nhiễu xạ thu được trên màn ảnh lớn hơn hay nhỏ hơn so với độ sáng tại chỗ đó khi không có màn chắn.
Bài 3.2.
Ánh sáng đơn sắc có bước sóng là 500nm, chiếu vuông góc vào một khe có bề rộng 0,02mm. Tìm bề rộng của ảnh khe sáng trên màn ảnh đặt cách khe 1m (thấu kính đặt sát khe sáng).
Bài 3.3.
Chiếu một chùm tia sáng song song có bước sóng là 500nm thẳng góc với một cách tử nhiễu xạ. Gần cách tử có đặt một thấu kính hội tụ. Khoảng cách từ màn đến thấu kính bằng 1m. Khoảng cách của hai vạch cực đại của quang phổ bậc nhất bằng 20,2cm. Xác định:
a. Chu kỳ d của cách tử.
b. Số vạch trên một mm của cách tử.
Bài 3.4.
Chiếu ánh sáng đơn sắc bước sóng =0,5m vào một lỗ tròn bán kính
chưa biết. Nguồn sáng điểm đặt cách lỗ tròn 2m, sau lỗ tròn 2m đặt màn quan sát. Hỏi bán kính của lỗ tròn bằng bao nhiêu để tâm của hình nhiễu xạ là tối nhất.
Bài 3.5.
Một nguồn sáng điểm chiếu ánh sáng đơn sắc bước sóng =0,5m vào một lỗ tròn có bán kính r=1mm. Khoảng cách từ nguồn sáng đến lỗ tròn R=1m. Tìm khoảng cách từ lỗ tròn đến màn quan sát để lỗ tròn chứ a ba đới Fresnel.
Bài 3.6.
Một màn ảnh đươc
đ ặt cách nguồn sáng điểm đơn sắc bước s óng
=0,5m một khoảng 2m. Chính giữa màn ảnh và nguồn sáng đ ặt một lỗ tròn
đường kính 0,2cm. Tìm số đới cầu Fresnel mà lỗ tròn chứ a đươc.
Bài 3.7.
Đặt một màn quan sát cách một nguồn sáng điểm phát ra ánh sáng đơn
sắc bước sóng =0,6m một khoảng x. Chính giữa khoảng x đặt một đia
tròn
nhỏ chắn sáng đường kính 1mm. Hỏi x bằng bao nhiêu để điểm M0 trên màn
quan sát có độ sáng gần giống như chưa đ ặt đia tròn , biêt́ điêm̉ M0và nguồn
sáng đều nằm trên truc
Bài 3.8.
của đia
tròn.
Một chùm tia sáng đơ n sắc song song bước sóng λ=0,589m chiếu thẳng
góc với m ột khe hep có bề r ộng b=2m. Hỏi những cực tiểu nhiễu xạ được
quan sát dưới những góc nhiêu
Bài 3.9.
xa ̣bằng bao nhiêu? (so với phương ban đầu)
Chiếu một chùm tia sáng đơn sắc song song vuông góc với m ột khe hep.
Bước sóng ánh sáng bằng 16 bề rộng của khe hep
. Hỏi cực tiểu nhiễu xạ thứ
ba đươc quan sát dưới góc lệch bằng bao nhiêu?
Bài 3.10.
Một chùm tia sáng đươc
rọi vuông góc với m ột cách tử . Biết rằng góc
nhiêu
xa ̣đối với vac̣ h quang phổ λ1=0,65m trong quang phổ b ậc hai bằng
φ1=450. Xác điṇ h góc nhiêu quang phổ bậc ba.
Bài 3.11.
xa ̣ứ ng với vac̣ h quang phổ λ2=0,5m trong
Cho một cách tử p hẳng có chu kỳ cách tử d=2μm. Sau cách tử đ ặt một
thấu kính hội tu,
trên màn quan sát đặt taị mặt phẳng tiêu của thấu kính người
ta quan sát thấy khoảng cách giữa hai quang phổ b ậc nhất ứ ng với bước sóng
λ1=0,4044μm và λ2 = 0,4047μm bằng 0,1mm. Xác điṇ h tiêu cự của thấu kính.