Tổng Hợp Dao Động Bằng Phương Pháp Giản Đồ Vectơ

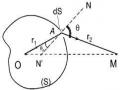
Dao động sáng do dS gây ra tại M là:

dx(M ) a(M )cos(t r1 r2 ) (3.1)

v

trong đó a(M ) là biên độ dao động sáng do nguồn dS gây ra tại M.

Biên độ a(M ) phụ thuộc vào các đại lượng dS, r1, r2, , 0 theo biểu thức:

a(M ) A(,0 )dS

r1r2

(3.2)

Có thể bạn quan tâm!

• Giao Thoa Gây Bởi Bản Mỏng Có Bề Dày Không Đổi. Vân Cùng Độ Nghiêng
• Hai Tia Phản Xạ Từ Cùng Một Tia Tới Tại Mặt Trên Và Mặt Dưới Của Bản Mỏng Không Khí Cho Hệ Thống Vân Tròn Newton
• Hiện Tượng Nhiễu Xạ Ánh Sáng. Nguyên Lí Huygens- Fresnel
• Vị Trí Các Cực Đại, Cực Tiểu Trong Nhiễu Xạ Qua Nhiều Khe
• D Sin   K  , D Là Khoa ̉ Ng Cách Giư ̃ A Hai Nút Man
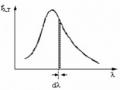
• Đu ̛ Ơ ̀ Ng Đ Ặc Tru ̛ Ng Phổ Phát Xạ Cu ̉ A Vật Đen Tuyệt Đối

Xem toàn bộ 258 trang tài liệu này.

Thực nghiệm chứng tỏ rằng năng lượng sáng phát ra theo phương vuông góc với dS là mạnh nhất, do đó nếu , 0 càng nhỏ thì A càng lớn.

Dao động sáng tổng hợp tại M là:

x dx(M ) A(,0) cos(t r1r2)dS (3.3)

(S ) r1r2v

Như vậy nguyên lí Huyghen-Fresnel cho phép nghiên cứu cường độ của sóng tổng hợp theo các phương khác nhau trong trường hợp sóng ánh sáng truyền tự do (truyền thẳng) cũng như khi gặp vật cản (nhiễu xạ).

Tuy nhiên việc giải trực tiếp bài toán này khá phức tạp vì rằng biên độ và pha ban đầu của các sóng thứ cấp phụ thuộc vào nhiều đại lượng. Ðể thay cho những tính toán phức tạp, Fresnel đưa ra phương pháp chia mặt (không tuỳ ý) thành những đới với điều kiện đặc biệt và được gọi là phương pháp đới cầu Fresnel.

3.2. PHƯƠNG PHÁP ĐỚI CẦU FRESNEL

3.2.1. Cách chia đới

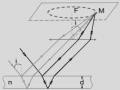
Xét nguồn sáng điểm S phát ánh sáng đơn sắc và điểm đươc

chiế u sáng

M. Lấy S làm tâm dưng m ặt cầu Σ bao quanh S, bán kính R < SM. Đặt

MB = b. Lấy M làm tâm vẽ các mặt cầu Σ0, Σ1, Σ2... có bán kính lần lươt là

b, b , b  2 , ... trong đó là bước sóng do nguồn S phát ra. Các mặt cầu

2 2

Σ0, Σ1, Σ2... chia mặt cầu Σ thành các đới goi là đới cầu Fresnel (ví dụ: đới cầu

thứ nhất là BM1M'1, đới cầu thứ hai là M1M'1M'2M2 ...).

S

B

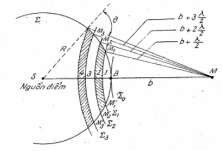
Hình 3.6. Cách chia đới cầu Fresnel

3.2.2. Tính biên độ tổng hợp

M

b

Trước hết, ta hãy tính bán kính của các đới cầu và từ đó chứng minh rằng theo cách chia đới Fresnel thì diện tích của mọi đới đều bằng nhau.

Ta có bán kính đới cầu thứ k là:

2 R2  (R h )2

k k

Mặt khác:

2 r2  (b h )2  (b 

Hình 3.7

2  (b h )2

k k k

k 2 ) k

k

R2  (R h )2  (b 

k ) 2

k

2  (b h )2

k k

 2Rh h2

k k



kb k

2 2

2 2

4

 2bh h2

2Rhk kb k

4  2bhk

2

k

Vì b nên với k không quá lớn có thể bỏ qua số hạng 2

4

phải. Do đó ta được:

ở vế

2Rhk kb  2bhk

hk

kb

2(R b)

(3.4)

k

Xét các đới cầu có k nhỏ, nghĩa là h2 rất nhỏ. Vậy:

2 R2  (R h )2  2Rh h2  2Rh

k k

2 kRb

k k k

(3.5)

k R b

tiếp.

Vậy bán kính các đới cầu tỉ lệ với căn bậc hai của các số nguyên liên

Diện tích của chỏm cầu thứ k (MkM'kB) là:

S  2R2 hk k R

 2Rhk

R kb

R b

Diện tích của đới cầu thứ k (M'k-1Mk-1MkM'k) là:

S S S

R kb

R (k 1)bR b

k k k1

R b

R b

R b

Ta thấy Sk không phụ thuộc vào k, nghĩa là diện tích các đới cầu đều bằng nhau và bằng:

Sk

R b

R b

(3.6)

Theo nguyên lí Huygens, mỗi đới cầu trở thành nguồn sáng thứ cấp phát ánh sáng tới điểm M. Gọi ak là biên độ dao động sáng do đới cầu thứ k gây ra tại M. Khi k tăng, các đới cầu càng xa điểm M và góc nghiêng θ tăng, do đó ak giảm:

a1 a2 a3 a4 ... (3.7)

khi k khá lớn thì ak  0.

Vì khoảng cách từ đới cầu đến điểm M và góc nghiêng θ tăng rất ch ậm nên ak giảm chậm, ta có thể coi ak do đới cầu thứ k gây ra là trung bình cộng của ak-1 và ak+1:

a 1 (a

a ) (3.8)

k 2 k1

k1

Khoảng cách của hai đới cầu kế tiếp tới điểm M khác nhau . Các đới

2

cầu đều nằm trên m ặt sóng Σ, nghĩa là pha dao đ ộng của tất cả các điểm trên mọi đới cầu đều như nhau . Kết quả , hiệu pha của hai dao đ ộng sáng do hai

đới cầu kế tiếp gây ra tai

M là:

 2(L1 L2 ) 2

2

Như v ậy hai dao động sáng đó ngươc pha nhau nên chúng sẽ khử lân

nhau. Vì M ở khá xa mặt Σ, ta coi các dao động sáng do các đới cầu gây ra tai

M cùng phương, do đó biên độ dao động sáng tổng hơp M sẽ là:

do các đớ i gây ra tai

a a1 a2 a3 a4 a5 a6... (3.9)

3.2.3. Phương pháp giản đồ vectơ

Việc khảo sát tác dụng của toàn bộ mặt sóng tại điểm M trên đây có thể được tiến hành theo cách vẽ Fresnel. Ở đây phương pháp này tỏ ra rất tiện lợi khi cần tổng hợp một số vô cùng lớn dao động có một hiệu số pha xác định nào đó.

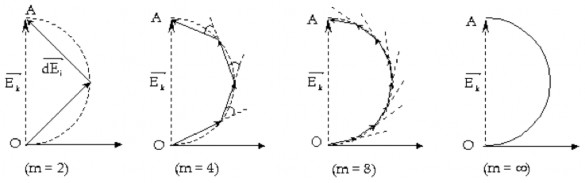
Hình 3.8. Tổng hợp dao động bằng phương pháp giản đồ vectơ

Ta tiếp tục chia mỗi đới cầu Fresnel thành m đới cầu nguyên tố dS có diện tích bằng nhau và rất bé để pha dao động của các đới cầu dS là không đổi.

Nhưng ta lại biết hai dao động phát ra từ hai đới Fresnel kề nhau gởi tới M là ngược pha nhau, nên pha dao động của các đới nguyên tố dS gửi tới M tăng dần từ 0 đến , hiệu số pha giữa hai đới nguyên tố kề nhau sẽ là n.

Do diện tích các đới được chọn bằng nhau nên biên độ của các dao động chỉ phụ thuộc vào góc (góc giữa pháp tuyến của dS với phương đến M), và sự phụ thuộc này không đáng kể do góc thay đổi rất nhỏ, do vậy các vectơ dao động có cùng độ dài. Biết độ dài của các vectơ và góc giữa hai vectơ kế tiếp ta dùng phương pháp vẽ giản đồ Fresnel để tổng hợp dao động sáng.

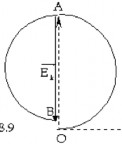
Nếu chọn gốc pha tại điểm O thì tổng các dao động ứng với đới cầu Fresnel thứ nhất sẽ là nửa chu vi của một đa giác đều. Nếu m thì nửa chu vi của đa giác đều trở thành nửa đường tròn (Hình 3.8), vectơ OA biểu diễn dao động phát đi từ đới Fresnel thứ nhất đến M.

Các dao động gởi đến M từ đới Fresnel thứ hai tạo thành trên giản đồ của Hình 3.9 nửa đường tròn có đường kính AB nhỏ hơn OA một ít vì a1 a2 . Như vậy tác dụng của hai đới Fresnel đầu tiên tại M được xác định bởi vectơ

tổng hợp OB OA AB. Cứ tiếp tục cách dựng này đối với

Hình 3.9

đới Fresnel tiếp theo, mỗi đới gửi đến M một dao động ngược pha với dao đọng gửi đến từ đới trước nó và coi rằng biên độ dao động giảm một cách liên tục từ đới Fresnel này sang đới Fresnel tiếp theo, thì tổng tất cả các dao động gửi đến M do toàn bộ mặt sóng tạo thành một đường xoắn ốc có điểm tiệm cận C ở chính giữa OA. Kết quả này ta cũng nhận được khi cộng đại số các biên độ theo phương pháp đới cầu Fresnel.

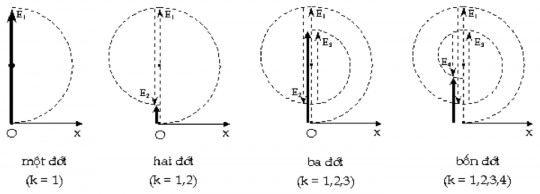
Hình 3.10

3.3. NHIỄU XẠ GÂY BỞI CÁC SÓNG CẦU

Dùng phương pháp đới cầu Fresnel có thể giải thích được hiện tượng nhiễu xạ xuất hiện khi một phần mặt sóng ánh sáng lan truyền bị vật cản chắn lại.

Bây giờ ta dùng phương pháp đới cầu Fresnel để giải thích hiện tượng nhiễu xạ của sóng cầu do các vật cản có hình dạng khác nhau. Hiện tượng nhiễu xạ này quan sát được ở gần vật cản và lần đầu tiên được Fresnel nghiên cứu, nên còn được gọi là nhiễu xạ Fresnel.

3.3.1. Nhiễu xạ qua lỗ tròn

a. Bố trí thí nghiệm

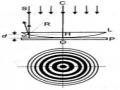
Đặt một miếng bìa dày có khoét một lỗ tròn nhỏ song song với màn quan sát và chắn giữa nguồn sáng điểm O và màn quan sát (Hình 3.11). Quan sát ánh sáng thu được tại vị trí điểm M trên màn quan sát với OM nằm trên trục của lỗ tròn.

b. Hiện tượng

Tại M có thể là sáng hơn hoặc tối hơn so với khi không có màn chắn tùy theo kích thước của lỗ tròn và vị trí của màn quan sát.

c. Giải thích

Theo phương pháp đới cầu Fresnel ta có biên độ sáng tổng hợp tại M là:

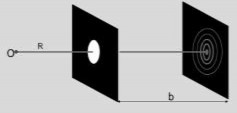
Hình 3.11. Nhiễu xạ qua lỗ tròn

Hình 3.12. Phân bố cường độ ảnh nhiễu xạ qua lỗ tròn

a a1 a2 a3 a4 a5 a6...

Do có miếng bìa chắn sáng nên sẽ có một số đới cầu cuối cùng trong biểu thức biên độ tổng hợp bị che khuất. Khi đó, biểu thức biên độ sáng tại M là:

a a1 a2 a3 a4 a5 a6... an

dấu "+" ứng với n lẻ, dấu "-" ứng với n chẵn.

Biểu thức () vẫn đúng cho trường hợp không có màn chắn, trong đó

n , an  0 .

Đối với k lẻ, tách:

a ak ak

k 2 2

Biểu thức biên độ được viết lại như sau:

a a1 a1 a a3 a3 a a5 a5 a a7 ...

2 2 2 2 2 4 2 2 6 2

an

2





nêú n  2 p 1

an1 a

nêú n  2q

î2n

a a1  ( a1 a a3 )  ( a3 a

a5 )  ( a5 a a7 ) ...

2 2 2 2

2 4 2 2 6 2

an

2





nêú n  2 p 1

an1 a

an

nêú n  2q

 2 n 2

Hình 3.13

Vì các biểu thứ c trong dấu ngo ặc bằng không, nên:

a a1 an

(3.10)

2 2

dấu "+" ứng với n lẻ, dấu "-" ứng với n chẵn.

Nhận xét:

 Khi không có màn chắn P hoặc kích thước lỗ tròn rất lớn : n , an  0

nên cường độ sáng taị M:

2

I0 ka

a2



k1

4

(3.11)

 Nếu lỗ chứ a số lẻ đới cầu:

I ka2 k( a1 an )2 I

(3.12)

2 2 0

điểm M sáng hơn khi không có màn P.

 Đặc biệt, nếu lỗ chứ a m ột đới cầu : n 1 a a1

I ka2  4I .

1

0

Cường độ sáng gấp 4 lần so với khi không có lỗ tròn , như vậy điểm

M rất sáng.

 Nếu lỗ chứ a số chẵn đới cầu:

I ka2 k( a1 an )2 I

(3.13)

2 2 0

điểm M tối hơn khi không có lỗ tròn.

 Đặc biệt, nếu lỗ tròn chứ a hai đới cầu thì : a a1 a2

 0 I  0,

2 2

điểm M tối hoàn toàn.

3.3.2. Nhiễu xạ qua đĩa tròn

a. Bố trí thí nghiệm

Ðặt một đĩa tròn chắn giữa một nguồn sáng điểm O và một màn quan

Hình 3.14. Nhiễu xạ qua đĩa tròn

sát đặt song song với đĩa (Hình 3.14). Quan sát ánh sáng thu được tại vị trí điểm M trên màn quan sát với OM nằm trên trục của đĩa tròn.

b. Hiện tượng

Tại M ta luôn thu được một điểm sáng khi đĩa tròn có kích thước không quá lớn và đĩa ở xa nguồn điểm O.

c. Giải thích

Hình 3.15. Phân bố cường độ ảnh nhiễu xạ qua đĩa tròn

Theo phương pháp đới cầu Fresnel ta có biên độ sáng tổng hợp tại M khi không có vật chắn sáng là:

a a1 a2 a3 a4 a5 a6...