Gương Fresnel Hình 2.10. Lưỡng Thấu Kính Bile

Tc là bước sóng ánh sáng trong chân không.

Phương trình (2.2) đươc

2.1.4. Cường độ sáng

goi

là hàm sóng ánh sáng.

Cường độ sáng đặc trưng cho đ ộ sáng taị mỗi điểm trong không gian có sóng ánh sáng truyền qua.

Điṇ h nghiã :

Cường đ ộ sáng tai

m ột điểm là đai

Có thể bạn quan tâm!

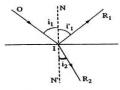
• Định Luật Về Tác Dụng Độc Lập Của Các Tia Sáng
• Những Phát Biểu Tương Đương Của Định Luật Descartes
• Các Đại Lượng Trắc Quang Là Các Đại Lượng Dùng Trong Kĩ Thuật Đo Lường Ánh Sáng.
• Giao Thoa Gây Bởi Bản Mỏng Có Bề Dày Không Đổi. Vân Cùng Độ Nghiêng
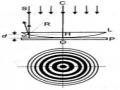
• Hai Tia Phản Xạ Từ Cùng Một Tia Tới Tại Mặt Trên Và Mặt Dưới Của Bản Mỏng Không Khí Cho Hệ Thống Vân Tròn Newton
• Hiện Tượng Nhiễu Xạ Ánh Sáng. Nguyên Lí Huygens- Fresnel

Xem toàn bộ 258 trang tài liệu này.

lươn

g có tri ̣số bằng nă ng lương

trung bình của sóng ánh sáng truyền qua một đơ n vi ̣di ện tích đặt vuông góc vớ i phươ ng truyền sáng trong một đơ n vi ̣thờ i gian.

Vì mật độ năng lượng của sóng đi ện từ tỉ l ệ thuận với bình phương biên

độ của véctơ cường đ ộ điện trường nên cường đ ộ sáng tai bình phương biên độ dao động sáng taị điểm đó:

I kA2

một điểm tỉ l ệ với

với k là hệ số tỉ lệ.

Khi nghiên cứ u các hi ện tươn

g giao thoa , nhiêu

xa ̣đ ặc trưng cho tính

chất sóng của ánh sáng , người ta chỉ c ần so sánh cường đ ộ sáng taị các điểm khác nhau mà không cần tính cu ̣thể giá tri ̣của cường đ ộ sáng, do đó qui ước lấy k  1:

I A2 (2.3)

2.1.5. Nguyên lí chồng chấ t các sóng

Khi có hai hay nhiều sóng ánh sáng truyền tới giao nhau taị m ột điểm

nào đó trong không gian thì sự tổng hơp̣ chồng chất các sóng. Nguyên lí này đươc

của các sóng tuân theo nguyên lí phát biểu như sau:

Khi hai hay nhiều sóng ánh sáng g ặp nhau thì từ n g sóng riêng biệt

không bi ̣các sóng khác làm cho nhiêu

loan

. Sau khi gặp nhau, các sóng ánh

sáng vân

truyền đi như cũ, còn tai

những điểm gặp nhau dao động sáng bằng

tổng các dao động sáng thành phần.

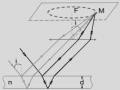
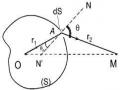
2.1.6. Nguyên lí Huygens

Môi

điểm trong không gian nhận đươc

sóng sáng từ nguồn sáng thưc

S truyền đến đều

trở thành nguồn sáng thứ cấp phát sóng sáng về phía trướ c nó

Nguyên lí Huygens đươc trên Hình 2.7.

mô tả đơn giản

2.2. GIAO THOA ÁNH SÁNG

2.2.1. Điṇ h nghiã

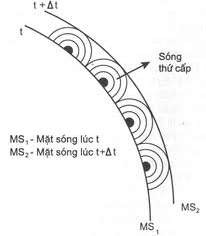
Hình 2.7

Hiện tươn

g giao thoa ánh sáng là hi ện tươn

g g ặp nhau của hai hay

nhiều sóng ánh sáng kết hơp

, kết quả là trong trườ ng giao thoa sẽ xuất hi ện

những vân sáng và những vân tối xen kẽ nhau.

Điều kiện giao thoa:

Hiện tươn

g giao thoa chỉ xảy ra đối với sóng ánh sáng kết hơp

. Sóng ánh

sáng kết hơp

là những sóng có hiệu pha không thay đổi theo thờ i gian.

Nguyên tắc tao

ra hai sóng ánh sáng kết hơp

là từ m ột sóng duy nhất

tách ra thành hai sóng riêng biệt. Dụng cụ để tạo ra các sóng ánh sán g kết

hơp: ví du ̣khe Young, gương Fresnel, lưỡng thấu kính Bile ...

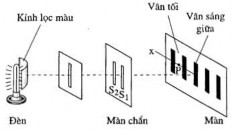
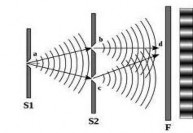
2.2.2. Khảo sát hiện tươn

Hình 2.8. Giao thoa Young.

g giao thoa

a. Điều kiện cưc

đaị , cưc

tiểu giao thoa

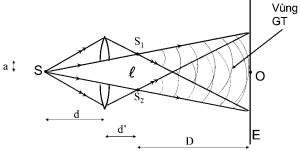
Hình 2.9. Gương Fresnel Hình 2.10. Lưỡng thấu kính Bile

Xét hai nguồn sóng ánh sáng đơn sắc kết hơp động sáng của chúng taị vi ̣trí của S1 và S2 là:

x(S1 ) A1 cost x(S2 ) A2 cost

S1 và S2. Phương trình dao

Tại M ta nhận đươc

hai dao động sáng:

x (M ) A cos(t 2L1 )

1 1

x2 (M ) A2



cos(t 2L2 )



với L1 và L2 là quang lộ tương ứng với đoan

đường d1 S1M, d2 S2 M .

Vì khoảng cách S1S2 nhỏ hơn rất nhiều so với khoảng cách từ m ặt phẳng của hai khe đến màn quan sát nên ta coi đây là trường hợp tổng hợp của hai dao động cùng phương, cùng tần số.

Dao động sáng tổng hợp tại M là:

x(M ) x1(M ) x2 (M ) Acos(t )

trong đó: A,tuân theo công thức tổng hợp dao động, theo đó:

A A  2A A cos

2 2

1 2

1 2

A 

với: 

(2.4)

2(L L ) (2.5)

2 1 1 2

Như vậy biên độ dao động sáng tổng hơp của hai dao động.

tai

M phụ thuộc vào hiệu pha

Nếu hai dao đ ộng cùng pha, hiệu pha  2k, thì biên độ dao động

sáng tổng hơp

tai

M sẽ có giá trị cực đại : A A1 A2 và cường đ ộ sáng tai

điểm M là cưc

đaị. Như vậy điều kiện cưc

đai

giao thoa là:

2(L L )  2k

1 2

L1 L2 kvới k=0,±1,±2... (2.6)

Nếu hai dao đ ộng ngươc pha , hiệu pha  (2k 1), thì biên độ dao

động sáng tổng hơp

taị M sẽ có giá tr ị cực tiểu : A A1 A2 và do đó cường

độ sáng cưc

tiểu. Như vậy điều kiện cưc

tiểu giao thoa là:

2(L L )  (2k 1)

1 2

d2

S2

d1

O

S1

M

L1

L2

 (k 1 )với k=0,±1,±2... (2.7)

2

b. Vị trí của vân giao thoa

Xét hệ thống khe Young như hình vẽ ,

đươc

đ ặt trong không khí . Xét điểm M trên

màn E, điểm M cách điểm O một khoảng là x.

Dễ thấy:

d2  (x a )2 

Hình 2.11. Vị trí của vân giao thoa

12 2 2

2ax

2



d2  (x 

a )2 ï2

d1 d2  2ax d1 d2 

d

1

d2



Xét: a D, x D có thể lấy gần đúng d1 d2  2D. Do hệ thống khe Young đặt trong không khí nên ta có:

L L d d

 2ax ax

(2.8)

1 2 1

2 2D D

Từ điều kiện cưc vân sáng và vân tối.

đaị, cưc

tiểu giao thoa ta dễ dàng tính đươc

vi ̣trí các

Vị trí các vân sáng (cưc đaị giao thoa):

L1 L2

ax kD

x k D, k  0, 1, 2... (2.9)

a

với k  0 là vân cưc

đai

trung tâm.

Vị trí các vân tối:

L L ax  (k 1 )

1 2 D 2

x  (k 1 ) D , k  0, 1, 2... (2.10)

2 a

Các vân sáng và tối nằm xen kẽ cách đều nhau về cả hai phía đối với vân sáng trung tâm. Đối với vân sáng , bậc giao thoa trùng với k. Đối với vân tối, khi k  0 bậc giao thoa trùng với k 1, khi k  0 bậc giao thoa trùng với k .

Khoảng cách giữa hai vân sáng kế tiếp:

i x

x  (k 1) Dk DD

(2.11)

k1 k

a a a

Tương tự, khoảng cách giữa hai vân tối kế tiếp cũng là i và i đươc

khoảng vân.

goi là

Các vân giao thoa thu được trên màn E là giao tuyến của hai họ mặt hypecbolic ứng với quỹ tích các điểm cực đại và cực tiểu giao thoa với màn

E. Vân sáng chính giữa là một đoạn thẳng, các vân khác là những đoạn hypecbol. Thông thường khoảng cách S1 S2 rất bé và màn quan sát đặt xa nên các đoạn hypecbol có thể coi như các đoạn thẳng. Các vân giao thoa là các

đoan

thẳng song song cách đều nhau.

Nếu dịch chuyển đồng thời S1 và S2 theo phương vuông góc với m ặt

phẳng hình vẽ thì h ệ thống vân chỉ trươt

trên mình nó và không thay đổi gì .

Do đó ta có thể thay hai nguồn sáng điểm S1 và S2 bằng hai nguồn sáng khe đặt vuông góc với mặt phẳng hình vẽ để cho hình ảnh giao thoa rò nét hơn.

c. Hệ vân giao thoa khi dùng ánh sáng trắng

Nếu nguồn sáng S1 và S2 phát ánh sáng trắng gồm moi

ánh sáng đơn sắc

có bước sóng  0, 4  0, 76m , thì mỗi ánh sáng đơn sắc sẽ cho m ột hệ vân giao thoa có màu sắc riêng và độ rộng i khác nhau.

Tại gốc tọa đ ộ O, ứng với x  0 điều kiện cực đại giao được thỏa mãn với mọi ánh sáng đơn sắc , tại O ta thu được tất cả các vân sáng đơn sắc trong

dải bước sóng  0, 4  0, 76m nên vân cưc đaị giữa là một vân sáng trắng.

Vì bề rộng khoảng vân i phụ thuộc vào bước sóng, bước sóng càng lớn thì khoảng cách giữa hai vân càng lớn. Do đó ở hai bên vân sáng trắng trung tâm, các hệ thống vân của những ánh sáng đơn sắc khác nhau sẽ nằm ở những vị trí khác nhau. Ứng với cùng một bậc vân sáng, vân tím ở gần vân trung tâm nhất, còn vân đỏ ở xa nhất tạo thành một dải màu trong tím, ngoài đỏ.

1

2

3

Hình 2.12. Giao thoa khi dùng ánh sáng trắng

Tại một vị trí nào đó, ta có thể thu được chồng chập nhiều vân sáng của các màu sắc khác nhau ứng với các bậc vân khác nhau. Càng xa vân sáng trung tâm, càng có nhiều vân sáng các màu chồng lên nhau, do đó màu sắc vân quan sát được bị nhòe dần khi xa vân sáng trắng ở trung tâm.

Bài toán 1:

Hai khe Young cách nhau một khoảng l  1mm , được chiếu bằng ánh

sáng đơn sắc có bước sóng  0, 6m . Màn quan sát được đặt cách mặt phẳng

chứa hai khe một đoạn D  2m .

a. Tìm khoảng vân giao thoa.

b. Xác định vị trí của ba vân sáng đầu tiên (coi vân sáng trung tâm là vân sáng bậc không).

c. Xác định độ dịch của hệ vân giao thoa trên màn quan sát nếu trước một trong hai khe đặt một bản mỏng song song, trong suốt có bề dày e  2m , chiết suất n  1,5.

Giải:

a. Khoảng vân giao thoa:

i D

l

 0, 6.106.2 103

 1, 2.103 m

b. Vị trí của vân sáng được xác định bởi công thức:

y kD, k  0, 1, 2, 3...

s l

s

y D 

1 l

0, 6.106.2 3



103 1, 2.10 m

ys2

ys3

2D 2,4.103 m l

3D 3,6.103 m l

c. Độ dịch chuyển của hệ vân

Khi đặt bản mỏng trong suốt trước một trong hai khe, hiệu quang lộ giữa các tia sáng từ hai khe đến một điểm trên màn thay đổi. Muốn biết hệ vân dịch chuyển như thế nào, ta phải tính hiệu quang lộ của hai tia sáng tại một điểm trên màn.

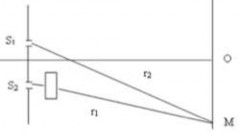
Từ hình vẽ ta có hiệu quang lộ:

L1L2(r1e) ner2 (r1r2) (n 1)e

Mà:

do đó:

r1 r2

L L

yl D

yl  (n 1)e

1 2 D

Vị trí vân sáng được xác định bởi điều kiện:

L L ysl  (n 1)e kykD(n 1)eD

1 2 D

s l l

Vị trí tối được xác định bởi điều kiện:

L L ytl  (n 1)e  (2k 1) Dy (2k 1) D(n 1)eD

1 2 D

Mặt khác:

2l t

2l l

y kD,

s l

y (2k 1)D

t l

Hệ vân dịch chuyển một khoảng:

y 

e(n 1)D l

 2.106.0,5.2 103

 2.103 m.

2.3. GIAO THOA GÂY BỞI BẢN MỎNG

Như ta đã biết nếu quan sát giao thoa với nguồn sáng điểm thì sẽ được vân giao thoa không định xứ rất rò. Tuy nhiên trong thực tế nguồn điểm khó thực hiện, trong nhiều trường hợp không thực hiện được. Hơn nữa trong thiên nhiên hiện tượng giao thoa trên bản mỏng thường được quan sát với nguồn rộng, chẳng hạn hiện tượng giao thoa trên các váng dầu, mỡ do ánh sáng tán xạ của một phần bầu trời. Trong trường hợp này thí nghiệm chứng tỏ rằng, hình ảnh giao thoa quan sát được rò nhất chỉ trong một miền không gian rất hẹp gần mặt bản mỏng và ra khỏi miền đó vân sẽ nhanh chóng biến mất. Vì vậy người ta gọi loại vân giao thoa này là vân giao thoa định xứ.

Khi nghiên cứu sự truyền ánh sáng qua các bản mỏng ta thấy một phần ánh sáng truyền qua bản mỏng, còn một phần phản xạ trở lại môi trường tới. Các tia phản xạ và truyền qua được tách ra từ một tia sáng tới nên thỏa mãn điều kiện kết hợp, nếu chúng gặp lại nhau sẽ xảy ra giao thoa ánh sáng. Để nghiên cứu hiện tượng giao thoa này trước hết chúng ta cần làm rò cách tính quang lộ của đường truyền tia sáng khi phản xạ qua hiện tượng giao thoa do phản xạ do Lloyd tiến hành.