Độ Tin Cậy Của Trạng Thái Cắt Đối Với Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Một Mode (Đường Nét Liền) Và Hai Mode (Đường Chấm



2i

t 

it

c 01 (t) c 00 (t)  sin e 2 ,

Có thể bạn quan tâm!

• Trạng Thái Lượng Tử Của Qubit Ứng Với Các Điểm Trên Mặt Cầu Bloch
• Kéo Lượng Tử Phi Tuyến Dựa Trên Các Dao Động Tử Phi Tuyến Kerr
• Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Một Mode
• Độ Tin Cậy Của Trạng Thái Cắt Trong Bộ Nối Phi Tuyến Tương Tác Phi Tuyến
• Xác Suất Để Hệ Tồn Tại Trong Các Trạng Thái Kiểu Bell
• Sự Tiến Triển Của Entropy Đan Rối (Đơn Vị Ebit) Của Trạng Thái Cắt Đối Với Các

Xem toàn bộ 144 trang tài liệu này.

00 01

 2 

it

it

01

t i

t e 2 e



c01

(t)  cos

2



sin

2  2

it

 ,

2

it

(2.22)

01

t i

t e 2 e



c10

(t)  cos

2



sin

2  2  2 ,



2i

t 

it

c 01 (t) c 00 (t)  sin e 2 .

11 10

 2 

cut a b

Khi các mode của hệ ban đầu ở trong các trạng thái (t  0)  1 0 và

cut a b

(t 11, ta cũng tìm được sự tiến triển của hệ đối với bộ nối được bơm hai mode có dạng tương tự với trường hợp được bơm một mode.

Để đánh giá chất lượng của phép cắt các trạng thái quang học, ta ứng

dụng độ tin cậy như một phép đo sự khác nhau giữa trạng thái cắt hai qubit

ˆcut (t)cutcut (t) , cho bởi (2.12), và trạng thái ra thực tế tính số từ:

ˆ (t)

(t)

được

(t)

 exp( iHˆt) | 0 | 0, (2.23)

a b

đối với không gian Hilbert hai mode. Độ tin cậy của trạng thái được định nghĩa bởi [68]:



1

2

F (, ˆcut ) Tr

ˆcut ˆ

ˆcut 2

, (2.24)



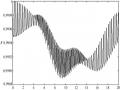
Độ tin cậy đối với phép cắt hoàn hảo bằng 1. Hình 2.3 trình bày độ tin cậy của trạng thái cắt. Từ Hình 2.3, ta thấy rằng độ tin cậy của trạng thái cắt xấp xỉ bằng một, tức là kết quả giải tích thu được là khá chính xác. Hơn nữa, độ tin cậy của trạng thái cắt đối với bộ nối phi tuyến được bơm hai mode nhỏ hơn so với bộ nối phi tuyến được bơm một mode, nghĩa là phép cắt đối với bộ nối được bơm một mode là chính xác hơn. Điều đó chứng tỏ rằng trạng thái cắt thu được có độ chính xác rất cao so với kết quả thu được trong [20].

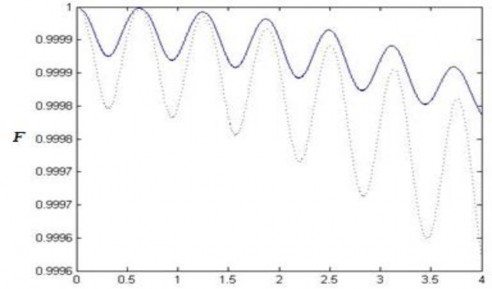
t [10-5s]

Hình 2.3: Độ tin cậy của trạng thái cắt đối với bộ nối phi tuyến tương tác tuyến tính được bơm một mode (đường nét liền) và hai mode (đường chấm chấm) với hệ số phi tuyến

8 5

a b  10 rad/s,  510 rad/s và các mode ban đầu ở trạng thái chân không

Chúng tôi sẽ sử dụng các biên độ xác suất phức thu được ở các phần trên để khảo sát sự tạo ra các trạng thái kiểu Bell ở phần tiếp theo.

2.1.2. Sự tạo ra trạng thái đan rối trong bộ nối phi tuyến tương tác tuyến tính

Chúng ta đã biết rằng sự đan rối của trạng thái thuần hai thành phần, mô

tả bởi ma trận mật độ



, có thể được mô tả bởi entropy von Neumann của

ma trận mật độ rút gọn

a Trb 

hoặc

b Tra , hoặc tương đương với entropy

Shannon của các hệ số Schmidt bình phương có dạng như sau [106]:

E Tr

ij 

1 a

log 2

aTrb

log 2

bSk

k

k

log 2 k

. (2.25)

Đối với trường hợp của trạng thái thuần hai qubit, giá trị của entropy đan rối thay đổi từ không đối với trạng thái không đan rối đến một ebit đối với trạng thái đan rối cực đại và nó có dạng đơn giản như sau [20]:

1

Eij(t) .log

2  (1).log

2 (1) , (2.26)

trong đó

1  1 C ij2

và ijijijijij

Từ đó, ta dễ dàng tìm

C

2

 2 c00 (t)c11 (t) c01 (t)c10 (t) .

được mối liên hệ giữa các entropy đan rối cho các trường hợp bộ nối được bơm một mode và hai mode bởi trường ngoài như sau:

E 11t E 00t , E 10t E 01t . (2.27)

1 1 1 1

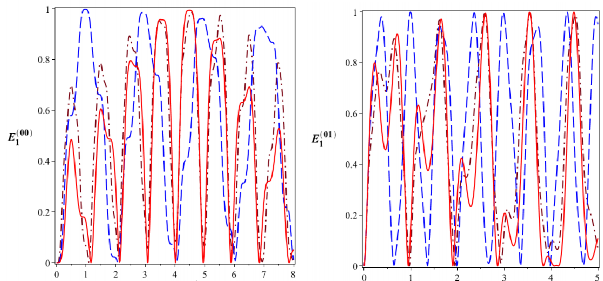
E

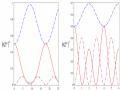
t [10-6s] t [10-6s]

Hình 2.4: Sự tiến triển của các entropy đan rối (đơn vị ebit)

00và

E

011

đối với bộ

1

nối phi tuyến tương tác tuyến tính được bơm một mode với

 106 rad/s,

 0

 106 rad/s (đường nét gạch) và

 106 rad/s,  210 6 rad/s (đường gạch chấm)

Các entropy đan rối của hệ đối với các điều kiện đầu khác nhau được chỉ

1

ra ở Hình 2.4. Các kết quả của E00đối với bộ nối được bơm một mode (  0) và

hai mode ( ) giống với những kết quả đã được trình bày ở [20]. Các

entropy đan rối

E00và

E

011

tiến triển theo chu kỳ thời gian và xấp xỉ bằng 1 ebit

1

E

đối với các trạng thái đan rối cực đại và bằng không đối với các trạng thái không

đan rối. Khi

, các giá trị cực đại của

00và

E

011

là lớn nhất trong khi chúng

1

là bé nhất đối với

. Hơn nữa, entropy đan rối

E

011

có nhiều cực đại hơn

E00,

1

tức là

E

011

dao động nhanh hơn

E00. Hệ quả là, các trạng thái đan rối cực đại và

1

entropy đan rối thay đổi một cách đáng kể đối với các mode ban đầu ở trong các trạng thái khác nhau.

Như một hệ quả, cực đại của các entropy đan rối có giá trị thay đổi theo chu kỳ, trong đó có một số giá trị gần bằng 1 ebit tương ứng với sự hình thành

của các trạng thái Bell. Để thể hiện rò ràng hơn, ta có thể trình bày các trạng thái được tạo ra trong cơ sở

(t)

Bij

, (2.28)

4

cut

l1 l1

l 1

được mở rộng thành các trạng thái kiểu Bell có dạng như sau [20]:

B



ij

11

B



ij

31

1 0

2 a

1 0

2 a

1

0

1

b

b

a

a

1

ij,

1

0

b

b

ij,

ij

B



21

B



ij

41

1 1

2a

1 1

2a

0

1

0

b

b

a

a

0

1

b

b

0

ij,

ij.

(2.29)

l

So sánh (2.12) và (2.28), ta tìm được các hệ số khai triển bij :

bij 1 cij(t) icij(t), bij 1 cij(t) icij(t),

11 2 00 11

21 2 11 00

(2.30)

bij 1 cij(t) icij(t), bij 1 cij(t) icij(t).

31 2 01 10 41 2 10 01

Dễ dàng thấy rằng

b012 b002 và

b012 b002 , vì vậy các hình vẽ đối với xác suất

11 41 21 31

để hệ tồn tại trong các trạng thái kiểu Bell

B

0111

B

và

0121

không cần phải trình

bày. Xác suất tìm thấy hệ trong các trạng thái kiểu Bell được trình bày ở các hình từ 2.5 đến 2.7.

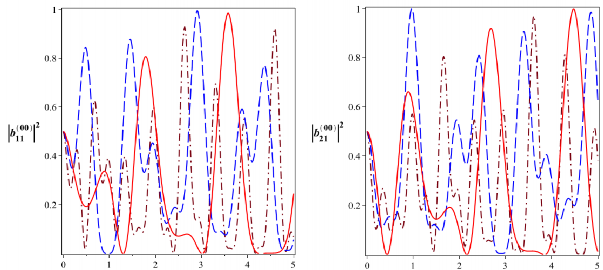
t [10-6s] t [10-6s]

Hình 2.5: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell

00

B

11

00

B

và

21

đối với

bộ nối phi tuyến tương tác tuyến tính được bơm một mode với

 106 rad/s,

 0

(đường nét liền) và hai mode với

 106 

rad/s (đường nét gạch) và

 106 rad/s,  210 6 rad/s (đường gạch chấm)

t [10-6s] t [10-6s]

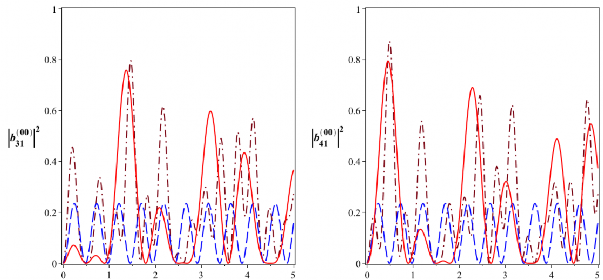
Hình 2.6: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell

00

B

31

00

B

và

41

đối với

bộ nối phi tuyến tương tác tuyến tính được bơm một mode với

 106 rad/s,

 0

 106 rad/s (đường nét gạch) và

 106 rad/s,  210 6 rad/s (đường gạch chấm)

t [10-6s] t [10-6s]

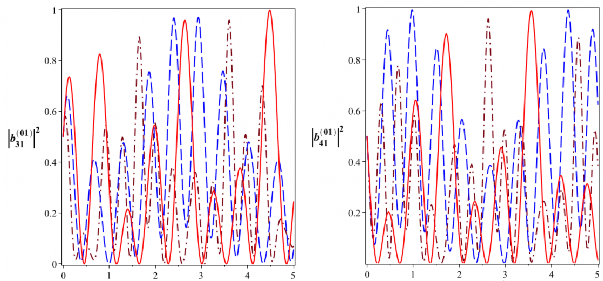
Hình 2.7: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell

B

0131

B

và

0141

đối với bộ

nối phi tuyến tương tác tuyến tính được bơm một mode với

 106 rad/s,

 0

 106 rad/s (đường nét gạch) và

 106 rad/s,  210 6 rad/s (đường gạch chấm)

Từ các hình vẽ ta thấy rằng khi bộ nối được bơm một mode (  0), đối

với các mode ban đầu ở trạng thái

, ta tìm được kết quả tương tự như kết

0 0

a b

quả trong [20] (Hình 2.5 và Hình 2.6). Đối với các mode ban đầu ở trạng thái

0 1

, xác suất tạo ra các trạng thái đan rối cực đại là hàm của thời gian cho các

a b

bộ nối điều khiển đơn mode và hệ cũng có thể tạo ra các trạng thái kiểu Bell đối

với các trạng thái

B

0131

B

và

0141

(Hình 2.7). Khi bộ nối được bơm hai mode, hệ

11

có thể tạo ra các trạng thái đan rối cực đại đối với các trạng thái B00,

00

B

21

(Hình 2.5) và

B

,

0131

B

0141

(Hình 2.7), nhưng hệ không thể tạo trạng thái đan rối

cực đại cho các trạng thái

00

B

và

,

31

00

B

và

41

(Hình. 2.6). Đặc biệt, khi

, các giá

11

trị cực đại của xác suất là lớn nhất đối với các trạng thái B00,

B

00

21

0141

B

trong khi chúng là nhỏ nhất đối với các trạng thái

B

00

,

31

00

B

và

và

41

. Hơn nữa, khi

tham số

, xác suất để hệ tồn tại ở trạng thái B00,

B

00

21

0131

B

0141

giảm,

11

B

trong khi xác suất để hệ thống tồn tại ở trạng thái

B

00

31

00

B

và

41

tăng.

1 0

1 1

và

Để không bị lặp lại, ở đây chúng tôi không trình bày các hình vẽ về xác suất để hệ tồn tại trong các trạng thái kiểu Bell và các entropy đan rối đối với

trường hợp các mode ban đầu ở các trạng thái

a b a b

bởi vì chúng đã

được trình bày trong các hình vẽ từ 2.4 đến 2.7 khi các mode ban đầu ở các

0 0

a b

và

a b

trạng thái 0 1 .

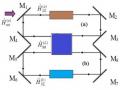
2.2. Bộ nối phi tuyến tương tác phi tuyến

2.2.1. Bộ nối phi tuyến tương tác phi tuyến được bơm một mode

2.2.1.1. Mô hình bộ nối phi tuyến tương tác phi tuyến được bơm một mode

Mô hình của một bộ nối phi tuyến được xem xét ở đây vẫn xây dựng dựa

trên hai dao động tử phi tuyến được đặc trưng bởi tính chất phi tuyến Kerr

a và

b tương ứng với hai mode a và b và mode a liên kết tuyến tính với trường

ngoài tương tự như bộ nối phi tuyến tương tác tuyến tính đã trình bày ở phần trên. Ở đây chỉ khác là các dao động tử này được liên kết phi tuyến với nhau. Khi đó, Hamiltonian của hệ chỉ khác so với bộ nối tương tác tuyến tính là thành

phần liên kết hai dao động tử là phi tuyến

ˆ ( NL)

H

int

thay cho thành phần tuyến tính

H

ˆ ( L)

int

và có dạng như sau [23]:

HˆHˆ

HˆaHˆbHˆ(NL) Hˆa, (2.31)

trong đó

0 NL NL

int

ext

Hˆ(a) aaˆ2aˆ2,

NL2

(2.32)

Hˆ(b) bbˆ2bˆ2,

NL2

int

HˆNLaˆ2bˆ2*bˆ2aˆ2,

ext

Hˆa aˆ*aˆ,

(2.33)

(2.34)

ở đây chúng tôi chỉ xét trường hợp không có tắt dần, sự tiến triển của hàm sóng phụ thuộc thời gian được biểu diễn dưới dạng trạng thái Fock n-photon như sau:



a b

(t)

cgh (t) g

g ,h0

h, (2.35)

trong đó,

cgh (t)

là các biên độ xác suất phức tìm hệ trong trạng thái g-photon của

mode a và trạng thái h-photon của mode b.

Sử dụng phương trình Schroedinger trong hình thức luận tương tác, ta được:

i d (t) Hˆa Hˆb Hˆ(NL) Hˆa (t)

, (2.36)

a

b

a

b

dt NL

NL int

ext

NL

h

,

Hˆa (t)

aaˆ2aˆ2



2

cgh

(t)g

a





h

2

g(g 1)cgh

(t)g

g ,h0

g ,h0

(2.37)

NL

Hˆb (t)

bbˆ2bˆ2



2

cgh

(t)g

b



h



h

,

2

h(h 1)cgh

(t)g

g ,h0

a

b

a

b



Hˆ(NL) (t) aˆ2bˆ2*bˆ2aˆ2c

g ,h0

(t) g h

int 

g ,h 0

gh a b





g ,h 0

(h  2)(h  1)g(g 1)cghg a h b



a

b

* 

g ,h 0

(g  2)(g  1)h(h 1)cgh

(t)g 

h 

(2.38)



h



g ,h 0

(h  2)(h  1)g(g 1)cg 2,h  2 g a b



a

h

,

b

* 

g ,h 0

(g  2)(g  1)h(h 1)c

g  2,h  2

(t)g

ext

Hˆa (t)

aˆ*aˆ

cgh

a

h

b

(t)g

g ,h 0



a

h

b

a

h

b



g ,h 0

g  1cgh

(t)g  1

* 

g ,h 0

gcgh

(t)g  1

(2.39)



a

h

b

a

h

.

b



g ,h 0

g  1c

g 1,h

(t)g

* 

g ,h 0

gcg 1,h

(t)g

Thay (2.37)-( 2.39) vào (2.36) ta thu được kết quả sau:

i d c

(t) 1 

g(g 1) 1 h(h 1)c

(t)

dtgh

2 a

2 b gh



*

(h  2)(h 1)g(g 1)cg 2,h2 (t)

(g  2)(g 1)h(h 1)cg 2,h2 (t)

(2.40)

*

g 1cg 1,h (t) 

gcg 1,h (t).

Đối với trường hợp này vì có quá trình tương tác của hệ với trường ngoài nên năng lượng của hệ không được bảo toàn. Do đó, khi hệ tiến triển theo thời gian sẽ có một số trạng thái có số lượng photon lớn. Khi giả thuyết rằng hệ số

phi tuyến

a,b , 

thì các phần tử tỉ lệ với a

và b

sẽ triệt tiêu do

Hˆa và

NL

H

ˆ b 

NL

tạo ra các mức năng lượng suy biến. Mặt khác, với giả thiết

a,b , ,

phương trình (2.40) chỉ ra rằng biên độ xác suất

cgh (t) sẽ dao động nhanh hơn

nhiều so với các biên độ xác suất khác khi g, h  2 . Do đó, áp dụng phương

pháp gần đúng sóng quay [107], người ta bỏ qua sự ảnh hưởng của biên độ xác

suất

cgh (t)

trong trường hợp này. Từ đó, sự tiến triển của hệ tương ứng với chỉ ba

trạng thái cộng hưởng sau

20, 12

và 0 2. Khi xét trong phép gần

a b a b

a b

đúng được sử dụng thì tiến triển của hệ chỉ khép kín trong ba trạng thái nói trên. Khi đó, hàm sóng của hệ được viết lại dưới dạng [108]:

pq(t)

cpq(t) 2 0

cpq(t) 1 2

cpq(t) 0 2

, (2.41)

cut

20 a b

12 a b

02 a b

p

q

a b

với p,q = 0,2 là ký hiệu của các mode ở trạng thái đầu và ta thu được các

phương trình chuyển động của các biên độ xác suất có dạng như sau:

Xem tất cả 144 trang.