Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Một Mode

Chương 2

CÁC TRẠNG THÁI ĐAN RỐI HÌNH THÀNH TRONG BỘ NỐI PHI TUYẾN KIỂU KERR

Trong chương này, chúng tôi nghiên cứu mô hình bộ nối phi tuyến gồm hai dao động tử phi tuyến liên kết tuyến tính hoặc phi tuyến với nhau và được bơm một mode hoặc hai mode bởi trường kết hợp ngoài. Bằng cách sử dụng hình thức luận NQS, ta thu được hàm sóng mô tả sự tiến triển của hệ là tổ hợp của các trạng thái Fock n-photon. Sự tiến triển của hệ theo thời gian có thể sinh ra các trạng thái đan rối cực đại gọi là các trạng thái kiểu Bell. Mô hình của chúng tôi được xem xét đối với các điều kiện đầu khác nhau của các biên độ xác suất.

2.1. Bộ nối phi tuyến tương tác tuyến tính

2.1.1. Mô hình bộ nối phi tuyến tương tác tuyến tính

2.1.1.1. Bộ nối phi tuyến tương tác tuyến tính được bơm một mode

Mô hình của một bộ nối phi tuyến kiểu Kerr được xem xét ở đây bao gồm hai dao động tử phi tuyến, tương tác tuyến tính với nhau và một trong hai dao động tử này (mode a) tương tác tuyến tính với trường ngoài kết hợp.

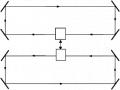
Về phương diện quang học bộ nối có cấu tạo và hoạt động như sau: Bộ nối phi tuyến là một thành phần của sợi quang phi tuyến hỗ trợ phân phối lại tín hiệu quang, có thể chia tín hiệu quang từ một thành hai hay nhiều tín hiệu và kết hợp tín hiệu quang từ hai hay nhiều thành một. Bộ nối phi tuyến kiểu Kerr được xét ở đây (Hình 2.1) gồm hai sợi quang phi tuyến không hấp thụ có lòi chứa môi trường phi tuyến Kerr, được đặc trưng bởi hai hệ số phi tuyến Kerr khác nhau

a và b . Các sợi quang này được ghép với bộ liên kết định hướng quang bốn

cổng, gồm hai cổng vào và hai cổng ra, được cấu tạo bằng cách gắn hai ống dẫn sóng với nhau bằng liên kết tuyến tính. Về nguyên tắc hai ống dẫn sóng của bộ liên kết định hướng phải được đặt gần nhau về không gian tới mức sóng đang

truyền trên ống này có thể cảm ứng truyền bên đường dẫn sóng kia [102], lúc đó ta có thể nói rằng có hiện tượng ghép mode giữa hai ống dẫn sóng đó. Thông thường hai ống dẫn sóng này chỉ có một không gian nhất định tại đó chúng rất sát nhau, gọi là chiều dài tương tác. Hệ số của liên kết tuyến tính giữa hai ống dẫn sóng phụ thuộc vào khoảng cách giữa hai ống, độ chênh lệch chiết suất và kích thước của ống. Các bản chia để tín hiệu vào có hệ số phản xạ R < 100%. Hệ số phản xạ, tán xạ trên mặt trước và sau của các mặt môi trường, hấp thụ của môi trường sẽ xác định hệ số tương tác của trường ngoài với hệ.

Chùm tia sáng vào bản chia M1, có hệ số phản xạ R < 100%, qua sợi quang phi tuyến ở mode a làm thay đổi pha truyền của các tia sáng. Các tia sáng tiếp tục phản xạ trên các gương M2 và M3 và đi vào bộ liên kết. Hoạt động của bộ liên kết tuân theo nguyên lý phản xạ, khúc xạ nên nếu trước khi vào bộ liên kết tín hiệu truyền trên nhánh a (b) của sợi quang phi tuyến thì sau bộ liên kết tín hiệu có thể vẫn truyền trên nhánh a (b) hoặc có thể chuyển sang truyền trên nhánh b (a) với độ lệch pha khác nhau. Sự kết hợp các tia sáng từ hai nhánh dẫn đến trạng thái giao thoa ở trong bộ nối này. Tùy thuộc vào cường độ của các tia sáng vào bản chia, ta sẽ thu được các cường độ tín hiệu ra khác nhau.

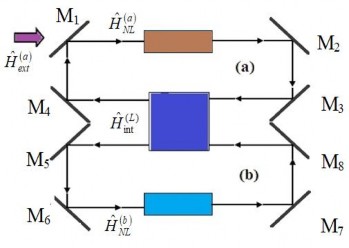
Hình 2.1: Mô hình bộ nối phi tuyến tương tác tuyến tính được bơm một mode

Khi đó, hệ này được mô tả bởi Hamiltonian có dạng ( =1) [20, 96, 103]:

HˆHˆ0Hˆ1,

Hˆ0aaˆ aˆ bˆbˆ,

b

(2.1)

HˆHˆa Hˆb Hˆ( L) Hˆa ,

trong đó:

1 NL

NL int

ext

Hˆ(a) aaˆ2aˆ2,

NL2

Hˆ(b) bbˆ2bˆ2,

NL 2 (2.2)

int

HˆL aˆbˆ*aˆbˆ,

ext

Hˆa aˆ*aˆ,

và aˆaˆvà bˆbˆlà các toán tử hủy (sinh) photon tương ứng với các mode a và b

của các dao động tử phi tuyến. Hamiltonian (2.1) đối với trường hợp tả bộ nối phi tuyến chuẩn [104, 105].

a

H  0

mô

ext

Trong bức tranh tương tác, sự tiến triển của hệ có thể được mô tả bởi

phương trình Schrodinger:

trong đó

i d (t)

dt

Hˆ1

b



(t)

, (2.3)

(t)

cmn (t) m a m,n 0

n, (2.4)

cmn (t) là các biên độ xác suất phức tìm hệ trong trạng thái m-photon của mode a

và trạng thái n-photon của mode b. Thay (2.4) vào (2.3) ta tìm được:



aaˆ2aˆ2

2

cmn

a

n

b

(t)m

a

2



m(m  1)cmn

a

n

b

(t)m

, (2.5)

m,n 0 m,n 0



bbˆ2bˆ2

2

cmn

a

n

b

(t)m

b





2

n(n 1)cmn

a

n

b

(t)m

, (2.6)

aˆbˆ*aˆbˆ

cmn

m,n 0

a

n

b

(t)m

m,n 0

m,n 0



a

b

a

b



m,n 0

n(m  1)cmn

(t)m  1

n 1

* 

m,n 0

m(n  1)cmn

(t)m 1

n  1

(2.7)



m(n  1)c (t) m n * n(m  1)c 

mn ,

m,n 0

m 1,n 1 a b

m,n 0

m 1,n 1 a b

n

aˆ*aˆ

cmn

(t)m

m,n 0



a

n

b

a

n

b



m,n 0

m  1cmn

(t)m  1

* 

a

b

m,n 0

mcmn

(t)m 1

(2.8)



a

n

b

a

n

.

b



m,n 0

mcm1,n

(t)m

* 

m,n0

m  1cm1,n

(t)m

Bằng cách thay các biểu thức từ (2.5) đến (2.8) vào (2.3) ta tìm được phương

trình chuyển động của biên độ xác suất

cmn t có dạng:

i d c

(t) 1 

m(m 1) 1 n(n 

dtmn

2 a

2b1)cmn (t)

*

n(m  1)cm 1,n1(t) 

m(n  1)cm 1,n1(t)

(2.9)

*

m  1cm 1,n (t) 

mcm 1,n (t).

1 0

Từ phương trình (2.9) có thể kết luận rằng sự tiến triển của hệ được bơm bởi trường ngoài cổ điển không chỉ được giới hạn trong các trạng thái hai photon mà còn các trạng thái nhiều photon hơn. Tuy nhiên, bằng cách sử dụng phương pháp kéo lượng tử phi tuyến [106], sự tiến triển của hệ có thể chỉ giới hạn trong

bốn trạng thái

00,

01,

và 11. Giả thiết các hệ số phi tuyến Kerr

a b

a b

a b

a b

a,b , , ta có thể giải thích sự tiến triển giữa bốn trạng thái này là sự dịch chuyển cộng hưởng. Hiện tượng này có thể chỉ ra một cách tường minh như sau:

Dưới sự giả thiết

a,b , 

và thời gian tiến triển ngắn, phương trình (2.9), với

những giá trị m, n  0,1, có thể xấp xỉ bằng:

i d c

t 1 

m m 11 n n 1c

t , (2.10)

dt mn

2 a

2 b mn

nghiệm của (2.10) là:

c t  exp i 1 

mm 11 n n 1t c

0. (2.11)

mn 2a

2 b mn



Bằng cách chọn điều kiện đầu

cmn (0)  0 , với

m, n  0,1, lúc đó

cmn (t)  0 . Ngược

lại, đối với các giá trị

m, n 0,1, các số hạng tỉ lệ với hệ số phi tuyến Kerr a

và b triệt tiêu do sự suy biến của Hamiltonian và do đó các số hạng tỉ lệ với 

và vẫn tồn tại. Lúc đó, hàm sóng của hệ sau khi “cắt” được viết dưới dạng đơn giản như sau:

ij t 

cij (t) 0 0

cij (t) 0 1

cij (t) 1 0

cij (t) 1 1

, (2.12)

cut

00 a b

01 a b

10 a b

11 a b

i, j  0,1 là kí hiệu cho trường hợp các mode ban đầu ở trong trạng thái ij . Từ phương trình (2.9), ta tìm được phương trình chuyển động cho biên độ

xác suất

cijtcó dạng như sau:

mn

i d cij (t) cij (t),

dt 00 10

i d cij(t) cij(t) cij(t),

dt 01 10 11

d

(2.13)

i cij (t) *cij (t) *cij (t),

dt 10 01 00

11 01

i d cij(t) *cij(t).

dt

Mặc dù các phương trình gần đúng (2.13) không phụ thuộc vào

a và

b , kết

quả thu được chỉ ra rằng tính chất phi tuyến Kerr đóng một vai trò chủ yếu trong quá trình cắt. Bằng cách giả thiết rằng cả hai dao động tử ban đầu ở trạng thái

a b

chân không ( (t  0)  0 0 ) và các tham số và là thực, khi đó nghiệm của

(2.13) cho các biên độ xác suất có dạng [20]:

c00(t) 1 cos 1t cos 2t ,

00 2 2

2





c00(t)  cos 1t  cos 2t 

01  2 2 ,

it

t 

(2.14)

c 00(t) 

2 sin1 sin2,

10 4 2 2 



c00(t) i  sin 1t 

sin 2t 

11 22 2

1 2 .



với

1 

2[22 2 ] ,

2 

2[22 2 ] , 

42 2 .

a b

Ở trên đã giả thuyết rằng cả hai mode ban đầu ở trạng thái chân không. Bây giờ, chúng tôi sẽ phân tích một sự tiến triển tổng quát hơn khi mà ban đầu một mode của hệ tồn tại trong trạng thái chân không và mode còn lại tồn tại

trong trạng thái Fock đơn photon ( (t 

độ xác suất (2.13) có dạng:

 01). Khi đó nghiệm của các biên



2



c01(t) c00(t)  cos 1t  cos 2t 

00 01

2 ,

c01(t) 1cos 1t cos 2t,

01 2 2

2

it

t 

(2.15)

c 01(t)  sin1 sin2,

10 22 2 1 2 



2



c01(t) c00(t) i2sin 1t sin 2t

11 10

4 2 .

Tiếp theo, ta sẽ xem xét sự tiến triển của hệ đối với các trường hợp khi

1 0

a b

a b

các mode ban đầu ở các trạng thái và 1 1 . Khi đó, sự tiến triển của hệ

đối với các trạng thái ban đầu này có dạng như sau:

10t 

11t 

cut cut

c000

10

11

a

a

0

0

b

b

c000

c010

10

10

a

a

1

1

b

b

c000

c011

01

01

a

a

0

0

b

b

c001

c001

01

00

a

a

1

1

,

.

b

b

c001

(2.16)

Trong phần tiếp theo, ta sẽ trình bày mô hình bộ nối phi tuyến tương tác tuyến tính được bơm hai mode bởi trường ngoài.

2.1.1.2. Bộ nối phi tuyến tương tác tuyến tính được bơm hai mode

Trong phần này chúng tôi tiếp tục mở rộng mô hình bộ nối đã được trình bày ở Hình 2.1 cho trường hợp cả hai mode a và b đều được kích thích bởi hai trường ngoài (Hình 2.2), trong khi mô hình trước đó chỉ một trong hai mode là được liên kết với trường ngoài. Khi đó, Hamiltonian mô tả hệ này có dạng sau [20, 21]:

HˆHˆHˆaHˆbHˆ(L) HˆaHˆb. (2.17)

0 NL NL

int

ext ext

Hamiltonian này về cơ bản giống với (2.1), ngoại trừ

ˆ (b)

H

ext

được cho bởi:

ext

Hˆ(b) bˆ*bˆ, (2.18)

mô tả liên kết tuyến tính của mode b với trường ngoài, trong đó tham số là hệ số của liên kết tuyến tính này.

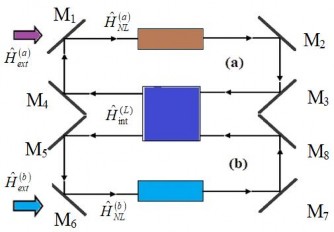
Hình 2.2: Mô hình bộ nối phi tuyến tương tác tuyến tính được bơm hai mode

Hoàn toàn tương tự như trường hợp bộ nối phi tuyến được bơm một mode, sự tiến triển của hệ được mô tả bởi Hamiltonian (2.17) có thể được cho bởi phương trình Schrödinger. Từ đó, ta dễ dàng tìm được hệ các phương trình

đối với các biên độ xác suất tương tác như sau [20]:

cmn (t)

của hàm sóng (2.4) trong hình thức luận

i d c

(t) 1 m(m 1) 1 n(n 1)c

(t)

dt mn

2 a

2 b mn

*

n(m  1)cm 1,n 1 (t) 

m(n  1)cm 1,n 1 (t)

(2.19)

*

*

m  1cm1,n (t) 

n  1cm,n 1 (t) 

mcm 1,n (t)

ncm,n 1 (t).

Tương tự như trường hợp một mode, ta giả thiết thời gian tiến triển ngắn và độ lớn

của các tham số , và là rất nhỏ so với các phi tuyến Kerr a và b . Khi đó,

phương trình (2.19) với trường hợp m, n  0,1 có thể xấp xỉ bằng (2.10) có nghiệm

là (2.11) sẽ triệt tiêu đối với điều kiện đầu

cmn (0)  0 . Do đó, dưới sự giả thiết ở

trên, hệ các phương trình (2.19) rút gọn thành bốn phương trình vi phân sau:

i d ckl (t) *ckl (t) *ckl (t),

dt 00 10 01

i d ckl (t) *ckl (t) *ckl (t) ckl (t),

dt 01 10

11 00

i d ckl (t) ckl (t) ckl (t) *ckl (t),

(2.20)

dt10

01 00 11

i d ckl (t) ckl (t) ckl (t),

dt11

01 10

k,l  0,1 là kí hiệu cho trường hợp các mode ban đầu ở trong trạng thái kl.

Giả thiết rằng tại thời điểm t = 0, cả hai mode của hệ đều ở trạng thái chân không, ta có thể tìm nghiệm giải tích của hệ phương trình (2.20). Để giải (2.20) cần tìm các giá trị không của đa thức bậc bốn, do đó, các nghiệm tổng quát của chúng là phức tạp và khó hiểu hơn. Tuy nhiên, nếu giả thiết rằng tất cả các hệ số liên kết là thực và các liên kết với trường ngoài có cường độ bằng nhau ( ), thì các nghiệm trở nên đơn giản và dễ hiểu hơn nhiều. Do đó, dưới các giả thiết này, các nghiệm của (2.20) có dạng sau [20]:

00

t i

t e

it



2 1

c00

(t)  cos

2



sin

2  2  2 ,

it

2it 
01 2  2it 
10		2 

Có thể bạn quan tâm!

• Các Trạng Thái Lượng Tử Hữu Hạn Chiều
• Trạng Thái Lượng Tử Của Qubit Ứng Với Các Điểm Trên Mặt Cầu Bloch
• Kéo Lượng Tử Phi Tuyến Dựa Trên Các Dao Động Tử Phi Tuyến Kerr
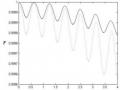
• Độ Tin Cậy Của Trạng Thái Cắt Đối Với Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Một Mode (Đường Nét Liền) Và Hai Mode (Đường Chấm
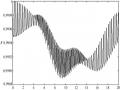
• Độ Tin Cậy Của Trạng Thái Cắt Trong Bộ Nối Phi Tuyến Tương Tác Phi Tuyến
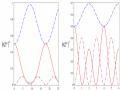
• Xác Suất Để Hệ Tồn Tại Trong Các Trạng Thái Kiểu Bell

Xem toàn bộ 144 trang tài liệu này.

c 00 (t) 

c 00 (t) 

sin 

sin 

e 2 ,

it

e 2 ,

it

(2.21)

00

t i

t e 21



c11

(t)  cos

2



sin

2  2  2 ,

0 1

trong đó  162 2 . Nếu tại thời điểm t = 0, một mode của hệ ở trạng thái

chân không còn mode kia ở trạng thái Fock đơn photon

(t 

thì

cut

a b

nghiệm của hệ phương trình (2.20) cho các biên độ xác suất có dạng sau:

Xem tất cả 144 trang.