i d cpq(t) 2cpq(t),
![]()
dt 20 02
i d cpq(t) cpq(t),
![]()
(2.42)
dt 12 02
i d cpq(t) 2*cpq(t) *cpq(t).
![]()
Có thể bạn quan tâm!
-
 Kéo Lượng Tử Phi Tuyến Dựa Trên Các Dao Động Tử Phi Tuyến Kerr
Kéo Lượng Tử Phi Tuyến Dựa Trên Các Dao Động Tử Phi Tuyến Kerr -
 Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Một Mode
Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Một Mode -
 Độ Tin Cậy Của Trạng Thái Cắt Đối Với Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Một Mode (Đường Nét Liền) Và Hai Mode (Đường Chấm
Độ Tin Cậy Của Trạng Thái Cắt Đối Với Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Một Mode (Đường Nét Liền) Và Hai Mode (Đường Chấm -
 Xác Suất Để Hệ Tồn Tại Trong Các Trạng Thái Kiểu Bell
Xác Suất Để Hệ Tồn Tại Trong Các Trạng Thái Kiểu Bell -
 Sự Tiến Triển Của Entropy Đan Rối (Đơn Vị Ebit) Của Trạng Thái Cắt Đối Với Các
Sự Tiến Triển Của Entropy Đan Rối (Đơn Vị Ebit) Của Trạng Thái Cắt Đối Với Các -
 Trung Bình Của Phương Trình Vi Phân Ngẫu Nhiên Với Nhiễu Trắng
Trung Bình Của Phương Trình Vi Phân Ngẫu Nhiên Với Nhiễu Trắng
Xem toàn bộ 144 trang tài liệu này.
dt02
20 12
Giả sử tại thời điểm t = 0, cả hai photon ở mode a và không có photon nào ở
mode b, tức là
c200 1 và
c200c200 0 ( ![]() (t
(t ![]()
cut
![]() 2
2![]()
![]() 0
0![]()
). Khi đó dễ
20
12 02
a
b
dàng giải hệ phương trình (2.42) để thu được nghiệm có dạng [23]:
c
2020
(t)
2 42 cos(t)
![]()
2 ,
c20(t) 2cos(t) 1,
(2.43)
12 2
c20(t) 2isin( t) ,
![]()
02
![]()
trong đó
2 42 . Hơn nữa khi giả sử tại thời điểm
t 0 , có một photon ở
mode a và hai photon ở mode b, có nghĩa là
c12(0) 1 và c12(0) c12(0) 0
12 20 02
cut a b
( ![]() (t
(t ![]()
![]() 1
1![]()
![]() 2
2![]() ), nghiệm của hệ phương trình (2.42) có thể tìm được dưới dạng:
), nghiệm của hệ phương trình (2.42) có thể tìm được dưới dạng:
c12(t) 2222cos(t),
20
12
c12(t)
22
![]()
1222cos(t),
2
(2.44)
c12(t) isin( t) .
![]()
02
Mặt khác nếu giả sử rằng tại thời điểm t 0 , không có photon nào ở mode a và cả hai photon
ở mode b, có nghĩa là
c020 1 và
c020c020 0 ![]() (t
(t ![]()
cut
![]() 0
0![]()
![]() 2
2![]()
, ta tìm
02
20 12
a
b
được nghiệm của hệ phương trình (2.42) có dạng:
c02(t) 2isin( t) ,
![]()
20
c02(t) isin( t) ,
![]()
(2.45)
12
02
c02(t) cos(t).
Để đánh giá độ chính xác của kết quả giải tích, ta sẽ tính độ tin cậy của
![]()
![]()
![]()
![]()
a b
trạng thái ra với trạng thái ban đầu là 2 0 . Khi đó, sự tiến triển theo thời gian
![]()
của trạng thái
(t)
có dạng sau:
![]()
![]()
![]()
(t)
exp( iHˆt) | 2![]()
![]()
0![]() . (2.46)
. (2.46)
b
a
Độ tin cậy của trạng thái ra được tính bằng biểu thức [85]:
1
![]()
![]()
2
F (, ˆcut ) Tr
ˆcut ˆ
ˆcut 2
, (2.47)
![]()
trong đó
![]()
![]()
ˆ (t)
(t) ,
ˆcut ![]() (t)
(t)![]() cutcut
cutcut ![]() (t)
(t) ![]() . (2.48)
. (2.48)
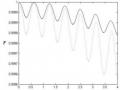
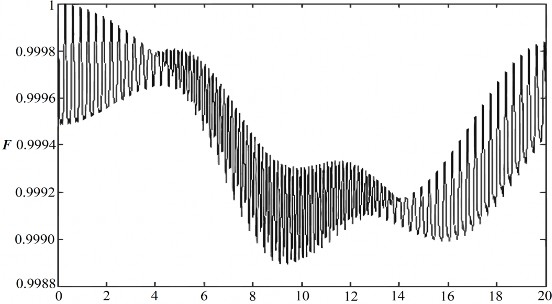
Đối với quá trình cắt hoàn hảo thì độ tin cậy sẽ cho giá trị bằng 1. Độ tin cậy của trạng thái cắt được thể hiện ở Hình 2.8.
t [10-6s]
7
Hình 2.8: Độ tin cậy của trạng thái cắt trong bộ nối phi tuyến tương tác phi tuyến
được bơm 1 mode. Trong trường hợp hệ số phi tuyến
1,5105 rad/s
a b 2,510 rad/s,
Có thể thấy rằng độ tin cậy của trạng thái cắt chỉ sai khác một lượng khoảng 10-3 so với giá trị cực đại bằng 1. Điều đó cho thấy trạng thái cắt thu được có độ chính xác rất cao, tương đương với kết quả thu được trong [23].
Ta sẽ sử dụng các biên độ xác suất từ (2.43) đến (2.45) để khảo sát sự tạo ra các trạng thái đan rối ở phần tiếp theo.
2.2.1.2. Sự tạo ra các trạng thái đan rối trong bộ nối phi tuyến tương tác phi tuyến được bơm một mode
a b
a b
2 0
a b
Ta có thể mong đợi rằng đối với mô hình được xem xét ở đây các trạng thái kiểu Bell có thể được tạo ra. Để nghiên cứu chi tiết hiện tượng này ta vẽ đồ
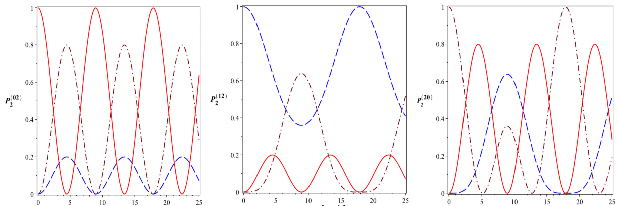
thị các xác suất đối với ba điều kiện đầu thái của hệ ở Hình 2.9.
![]() 0
0![]()
![]() 2
2![]() ,
,
![]() 1
1![]()
![]() 2
2![]() và
và ![]()
![]()
![]()
![]()
của ba trạng
t [10-6s] t [10-6s] t [10-6s]
![]()
![]()
![]()
![]()
0 2
a b
Hình 2.9: Các xác suất để hệ tồn tại trong các trạng thái (đường nét liền),
1 2
2 0
a b
a b
![]()
![]()
![]()
![]() (đường nét gạch) và
(đường nét gạch) và ![]()
![]()
![]()
![]()
(đường gạch chấm) với
5104 rad/s,
![]()
![]()
(t 0)
cut
![]() 0
0![]()
![]() 2
2![]()
( P02),
(t 0)
cut
![]() 1
1![]()
![]() 2
2![]()
( P12) và
(t 0)
cut
![]() 2
2![]()
![]() 0
0![]()
(P20)
![]()
![]()
![]()
![]()
2
2
2
2
2
a
b
a
b
a
b
a
2
b
2
0
và
a b
1
2
a b
2
0
a b
Từ Hình 2.9, có thể thấy rằng các xác suất này dao động và một số đồ thị cắt nhau tại những giá trị gần bằng 0,5. Điều này chỉ ra rằng các trạng thái kiểu Bell có thể được tạo ra trong trường hợp này. Cụ thể, ta quan sát được các cặp
2
0
a b
trạng thái ![]()
![]()
![]()
![]()
và ![]() 0
0![]()
![]()
![]()
(P02), ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ( P12) cũng như
( P12) cũng như ![]()
![]()
![]()
![]() và
và
2
0
2
a b
![]()
![]()
![]()
![]() ( P20) cắt nhau tại những giá trị gần bằng 0,5. Ngoài ra có thể xem xét
( P20) cắt nhau tại những giá trị gần bằng 0,5. Ngoài ra có thể xem xét
2 0
và
các tổ hợp khác của các trạng thái thuần được thảo luận ở đây. Chẳng hạn, các
1 2
trạng thái kiểu Bell bao gồm
![]()
![]() a
a ![]()
![]() b
b ![]()
![]() a
a ![]()
![]() b
b
có thể được xem xét. Sau khi xem
xét kĩ các kết quả của đồ thị ở Hình 2.9, ta thấy rằng các trạng thái kiểu Bell này
có thể đóng một vai trò trong sự tiến triển của hệ. Ta quan sát sự giao nhau của các đồ thị của các xác suất thích hợp, mặc dù các điểm cắt nhau của chúng tương ứng với giá trị xác suất gần bằng không hoặc một. Vì thế, đối với những
![]()
![]()
![]()
![]()
a b
khoảng thời gian này hệ gần như ở trạng thái thuần 0 2 . Tuy nhiên, có thể
![]()
![]()
a
2
b
a
2
thấy rằng đối với một số khoảng thời gian khác các xác suất này trở nên gần bằng 0,5, mặc dù chúng không cắt nhau. Cho nên, ta có thể mong đợi trạng thái kiểu Bell lại được tạo ra. Kết quả là các trạng thái kiểu Bell có thể được hình thành từ các cặp trạng thái của hệ được xét có dạng như sau:
![]()
![]()
B
pq
12
1 2
![]()
![]()
![]()
![]()
![]()
![]()
0
a
2 a b
![]() 0
0![]()
![]()
pq,
pq
![]()
![]()
B
22
1 2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
0
2
b
a
2
2 a b
![]() 0
0![]()
![]()
pq,
![]()
![]()
B
pq
32
1 2
![]()
![]()
![]()
![]()
![]()
0
2 a b
![]() 1
1 ![]()
pq,
pq
![]()
![]()
B
42
1 2
![]()
![]()
![]()
![]()
![]()
0
2 a b
![]() 1
1 ![]()
pq,
![]()
b
b
(2.49)
![]()
![]()
B
pq
52
1 2
![]()
![]()
![]()
![]()
![]()
0
2 a b
![]() 1
1![]()
![]() 2
2![]()
pq,
pq
![]()
![]()
B
62
1 2
![]()
![]()
![]()
![]()
![]()
0
2 a b
![]() 1
1![]()
![]() 2
2![]()
pq.
a
b
a
b
Xác suất để hệ tồn tại trong các trạng thái kiểu Bell được tính bởi biểu thức sau:
![]()
i 2
B
P(Bpq)
pqi 2
cut
(t)
2
![]()
. (2.50)
![]()
Trạng thái (2.41) có thể khai triển trong cơ sở các trạng thái Bell theo dạng:
![]()
![]()
(t)
b![]() Bpq
Bpq![]()
. (2.51)
6
cut
i 2 i 2
i1
b
Do đó, ta có thể tìm được các hệ số
pqi
có dạng:
bpq
1cpq(t) icpq(t),
bpq
1cpq(t) icpq(t),
![]()
![]()
12 2 20 02 22 2 20 02
bpq 1 cpq(t) icpq(t), bpq 1 cpq(t) icpq(t),
(2.52)
![]()
![]()
32 2 20 12 42 2 20 12
bpq
1cpq(t) cpq(t),
bpq
1cpq(t) cpq(t).
![]()
![]()
52 2 20 12 62 2 20 12
Sự tạo ra các trạng thái đan rối cực đại có thể được mô tả bởi entropy von Neumann như đã trình bày ở chương 1. Để áp dụng cụ thể cho việc tính độ đan rối hình thành trong bộ nối phi tuyến, ở đây ta lần lượt tính các đại lượng sau:
ˆab ![]()
![]() cutcut
cutcut ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
cpq2 0 2
2 0 cpqcpq* 0 2
2 1 cpqcpq* 0 2 0 2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
02 a bb a
02 12
a bb a
02 20
a bb a
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
cpqcpq* 1
2 2 0 cpq2 1 2
2 1 cpqcpq* 1 2 0 2
(2.53)
![]()
![]()
![]()
![]()
12 02
a bb a
12 a bb a
12 20
a bb a
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
cpqcpq* 2 0
2 0 cpqcpq* 2 0
2 1 cpq2 2 0
0 2 .
20 02
a bb a
20 12
a bb a
20 a bb a
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Từ đó có thể tính vết thành phần trên mode b như sau
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ˆbTraab a![]() 0
0 ![]() ab
ab ![]() 0
0![]() aa
aa![]() 1
1![]() ab
ab ![]() 1
1![]() aa
aa
2![]() ab
ab ![]() 2
2![]() a
a
![]()
![]()
![]()
![]()
cpq2 0
0 cpq2 cpq2 2 2 ,
(2.54)
20
với các trị riêng lần lượt của
ˆb
bb
là:
02 12
bb
0 ;
cpq2
và
cpq2 cpq2 1 cpq2 . (2.55)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1 2 20 3 02 12 20
Kết quả ta thu được biểu thức tính độ đan rối là:
pq
E2
(t) 2 log 2 2 3 log 2 3 . (2.56)
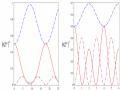
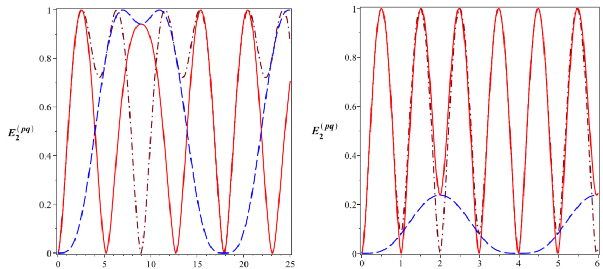
Sự tiến triển của entropy đan rối được trình bày ở Hình 2.10.
t [10-6s] t [10-6s]
Hình 2.10: Entropy đan rối (đơn vị ebit)
E
202
(đường nét liền),
12
E
2
(đường nét gạch)
E
2
và 02
(đường gạch chấm) với
5104 rad/s (Hình bên trái) và
5104 rad/s,
2.5105 rad/s (Hình bên phải)
E
Các kết quả của
202
ở Hình 2.10 trái tương tự với các kết quả tìm được
E
ở
trong [23]. Các entropy đan rối thay đổi theo chu kỳ của thời gian tùy thuộc vào các điều kiện đầu khác nhau và bằng 1 ebit đối với các trạng thái Bell, trong khi
các trạng thái tách ra có giá trị bằng không. Ngoại trừ cực đại thứ hai của
20
2
Hình 2.10 trái và các cực đại của
12
E
2
ở Hình 2.10 phải, giá trị của tất cả các cực
đại còn lại xấp xỉ bằng đơn vị, nghĩa là hệ có thể là nguồn của các trạng thái kiểu Bell. Như một hệ quả, giá trị của các entropy đan rối thay đổi một cách đáng kể đối với các điều kiện đầu khác nhau.
Xác suất để hệ tồn tại trong các trạng thái kiểu Bell với ba điều kiện đầu
![]()
cut a b
(t ![]()
![]() 2
2![]()
![]() 0
0![]() ,
,
![]() (t
(t ![]()
![]() 1
1![]()
![]() 2
2![]()
và ![]() (t
(t ![]()
![]() 0
0![]()
![]() 2
2![]()
được trình bày trong
cut a b
cut a b
các hình vẽ từ 2.11 đến 2.16.
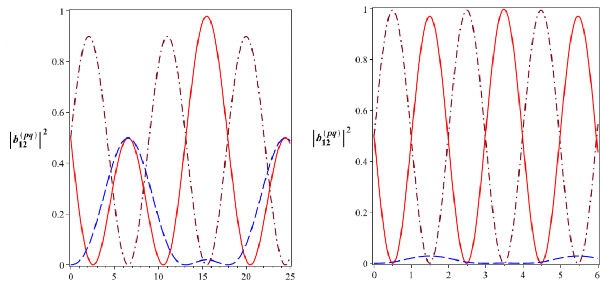
t [10-6s] t [10-6s]
![]()
B
Hình 2.11: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell
2012
(đường nét liền),
![]()
![]()
![]()
B
12
12
(đường nét gạch) và
02
![]()
![]()
B
12
(đường gạch chấm) với 5104 rad/s (Hình bên
trái) và 5104 rad/s, 2.5105 rad/s (Hình bên phải)
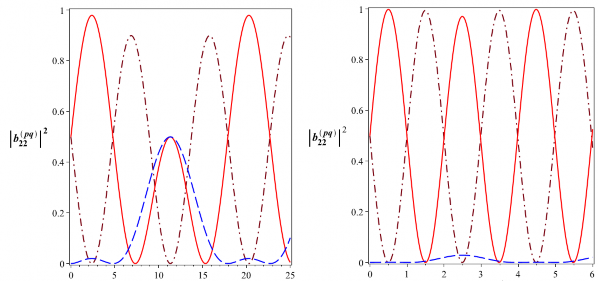
t [10-6s] t [10-6s]
Hình 2.12: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell
![]()
![]()
B
2022
(đường nét liền),
![]()
![]()
B
12
22
(đường nét gạch) và
02
![]()
![]()
B
22
(đường gạch chấm) với 5104 rad/s (Hình bên
trái) và 5104 rad/s, 2.5105 rad/s (Hình bên phải)
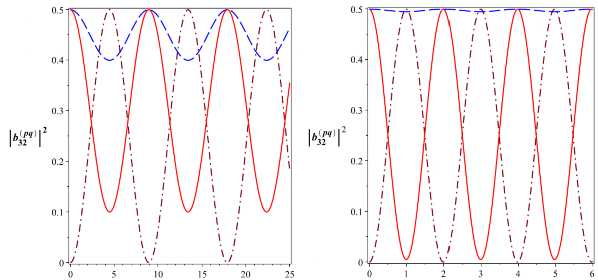
t [10-6s] t [10-6s]
Hình 2.13: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell
![]()
![]()
B
2032
(đường nét liền),
![]()
![]()
B
12
32
(đường nét gạch) và
02
![]()
![]()
B
32
(đường gạch chấm) với 5104 rad/s (Hình bên
trái) và 5104 rad/s, 2.5105 rad/s (Hình bên phải)
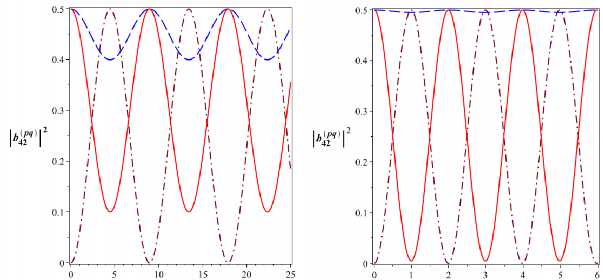
t [10-6s] t [10-6s]
Hình 2.14: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell
![]()
![]()
B
2042
(đường nét liền),
![]()
![]()
B
12
42
(đường nét gạch) và
02
![]()
![]()
B
42
(đường gạch chấm) với 5104 rad/s (Hình bên
trái) và 5104 rad/s, 2.5105 rad/s (Hình bên phải)
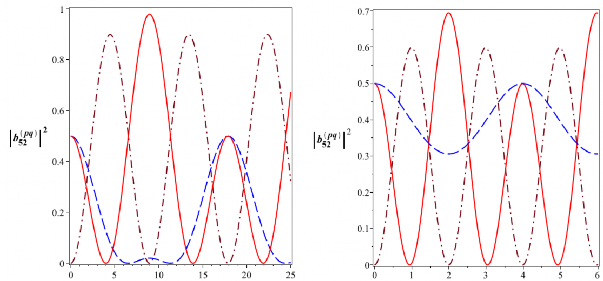
t [10-6s] t [10-6s]
Hình 2.15: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell
![]()
![]()
B
2052
(đường nét liền),
![]()
![]()
B
12
52
(đường nét gạch) và
02
![]()
![]()
B
52
(đường gạch chấm) với 5104 rad/s (Hình bên
trái) và 5104 rad/s, 2.5105 rad/s (Hình bên phải)