Sự Tiến Triển Của Entropy Đan Rối (Đơn Vị Ebit) Của Trạng Thái Cắt Đối

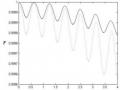
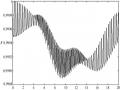
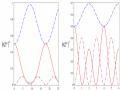
trạng thái đan rối. Khi β tăng, đỉnh thứ hai của

E20chia thành hai đỉnh và chúng

đạt giá trị xấp xỉ bằng đơn vị và chu kỳ của các entropy đan rối thay đổi. Do đó, sự hiện diện của β làm thay đổi các giá trị và vị trí của các đỉnh của entropy đan

rối. Hơn nữa, trong cùng một khoảng thời gian, các entropy đan rối có nhiều giá trị cực đại hơn so với các kết quả của [23].

02

Có thể bạn quan tâm!

Xem toàn bộ 144 trang tài liệu này.

và12

t [10-6s] t [10-6s]

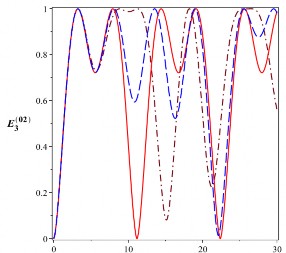
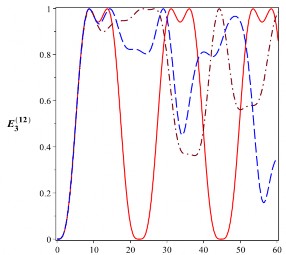
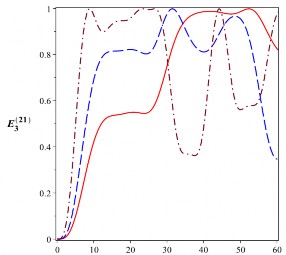
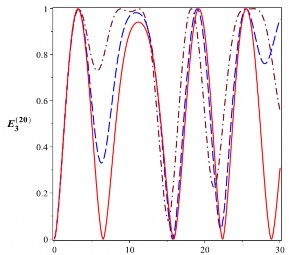
Hình 2.19: Sự tiến triển của entropy đan rối (đơn vị ebit) của trạng thái cắt đối với các

a b

trạng thái đầu là

( E02),

( E12),

( E21) và

( E20) với

a b

 4104 rad/s. Đường nét liền là cho  0 , đường nét gạch là cho

 2104 rad/s và đường gạch chấm là cho  4104 rad/s

a b

Các Hình từ 2.20 đến 2.25 chỉ ra các xác suất để hệ tồn tại trong các trạng

thái kiểu Bell

a b a

21và 2

mni3

(i=1,2,3,...,6) tương ứng với các trạng thái đầu 0 2

, 1 2,

t [10-6s] t [10-6s]

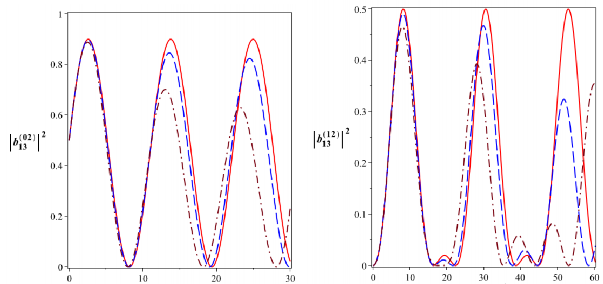
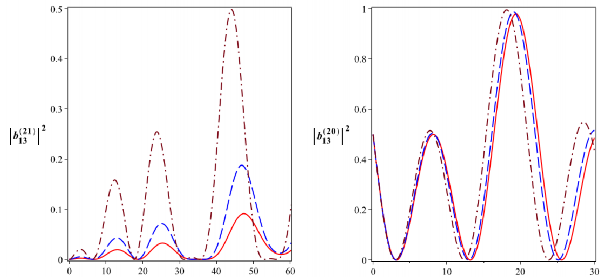
Hình 2.20: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell

02

a b

( b022 ),

12

( b122 ),

2113

( b212 ) và

2013

( b202 ) tương ứng với các trạng thái đầu

a b

2 1

2 0

a b

và

a b

12,

với  4104 rad/s. Đường nét liền là cho

 0 , đường

nét gạch là cho

 2104 rad/s và đường gạch chấm là cho

 4104 rad/s

t [10-6s] t [10-6s]

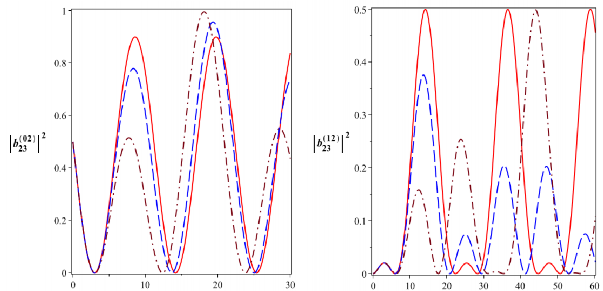
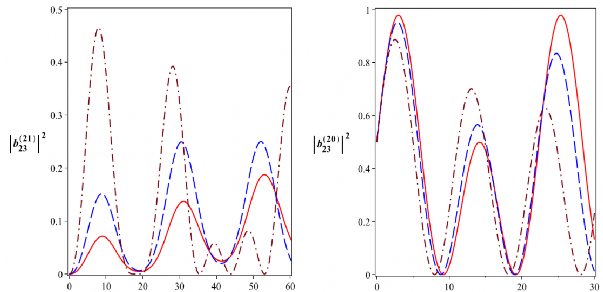
Hình 2.21: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell

02

a b

( b022 ),

12

( b122 ),

2123

( b212 ) và

2023

( b202 ) tương ứng với các trạng thái đầu

a b

2 1

2 0

a b

và

a b

12,

với  4104 rad/s. Đường nét liền là cho

 0 , đường

nét gạch là cho

 2104 rad/s và đường gạch chấm là cho

 4104 rad/s

t [10-6s] t [10-6s]

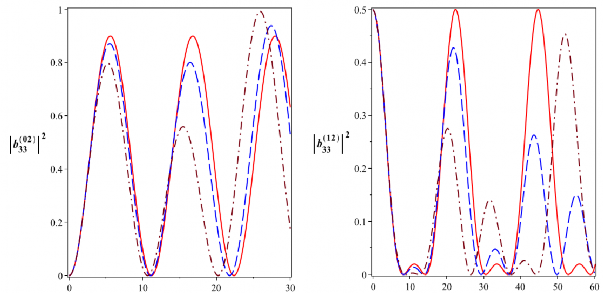
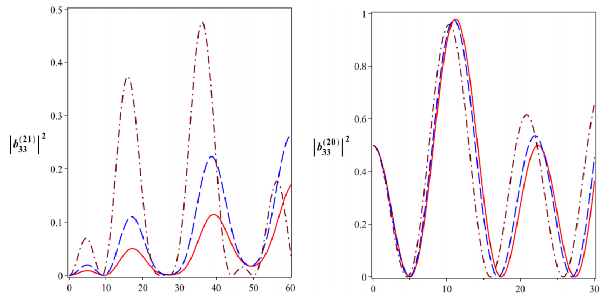
Hình 2.22: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell

02

a b

( b022 ),

12

( b122 ),

2133

( b212 ) và

2033

( b202 ) tương ứng với các trạng thái đầu

a b

2 1

2 0

a b

và

a b

12,

với  4104 rad/s. Đường nét liền là cho

 0 , đường

nét gạch là cho

 2104 rad/s và đường gạch chấm là cho

 4104 rad/s

t [10-6s] t [10-6s]

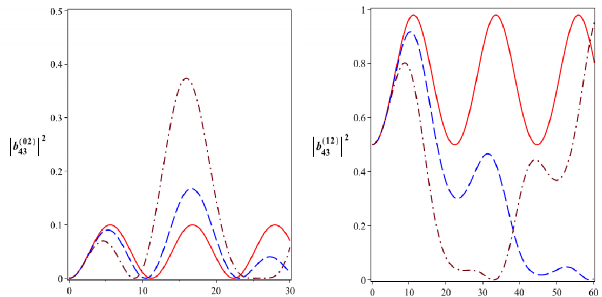
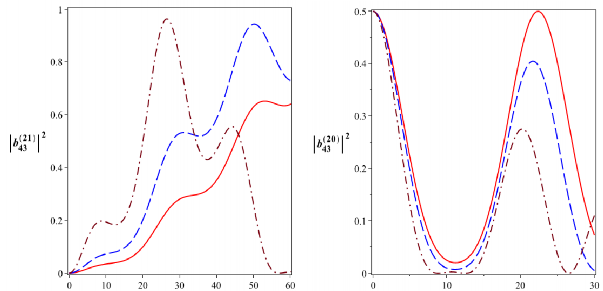
Hình 2.23: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell

02

a b

( b022 ),

12

( b122 ),

2143

( b212 ) và

2043

( b202 ) tương ứng với các trạng thái đầu

a b

2 1

2 0

a b

và

a b

12,

với  4104 rad/s. Đường nét liền là cho

 0 , đường

nét gạch là cho

 2104 rad/s và đường gạch chấm là cho

 4104 rad/s

t [10-6s] t [10-6s]

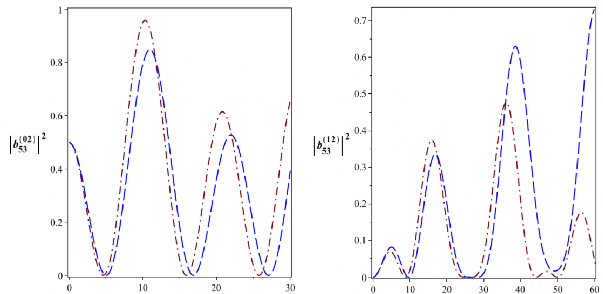
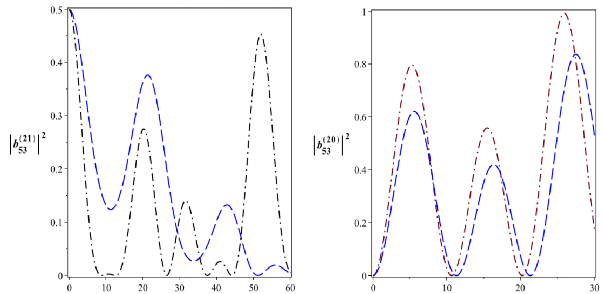
Hình 2.24: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell

02

a b

( b022 ),

12

( b122 ),

2153

( b212 ) và

2053

( b202 ) tương ứng với các trạng thái đầu

a b

2 1

2 0

a b

và

a b

12,

với

 4104 rad/s. Đường nét gạch là cho

 2104 rad/s và đường gạch chấm là cho  4104 rad/s

t [10-6s] t [10-6s]

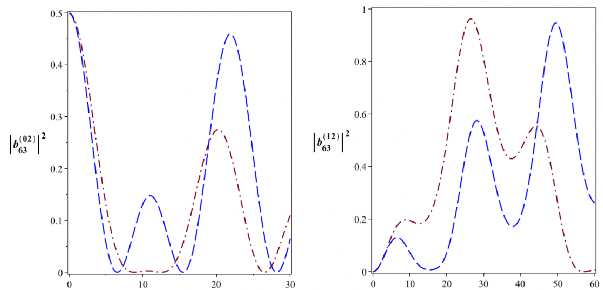
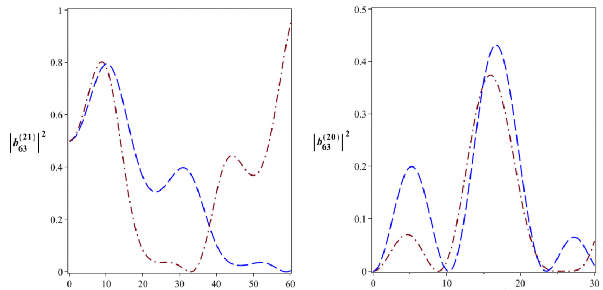
Hình 2.25: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell

02

a b

( b022 ),

12

( b122 ),

2163

( b212 ) và

2063

( b202 ) tương ứng với các trạng thái đầu

a b

2 1

2 0

a b

và

a b

12,

với

 4104 rad/s. Đường nét gạch là cho

 2104 rad/s và đường gạch chấm là cho  4104 rad/s

Khi β = 0, ta thu được kết quả của trường hợp bộ nối liên kết phi tuyến được bơm một mode đã trình bày ở phần 2.2.1. Đặc biệt, đối với trạng thái đầu

là 2 0 , kết quả thu được cho trường hợp β = 0 còn trùng với xác suất để hệ

tồn tại trong các trạng thái kiểu Bell được bơm một mode bởi trường ngoài được thảo luận ở [23]. Khi β = α, chúng tôi cũng thu được các xác suất để hệ tồn tại trong các trạng thái kiểu Bell được bơm bởi hai trường ngoài có cùng cường độ [109].

và

Từ các Hình vẽ 2.20 đến 2.25, ta thấy rằng các trạng thái đan rối cực đại

có thể được tạo ra cho cả bốn trạng thái đầu

02,

12,

với

a b

2 1

2 0

a b

và

những giá trị khác nhau của tham số β. Cụ thể, các trạng thái đan rối cực đại

02

và

2013

(Hình 2.20),

02

và

2023

(Hình 2.21),

02

và

2033

(Hình

2.22),

12

2143

(Hình 2.23),

02

2053

(Hình 2.24),

12

2163

(Hình 2.25) có thể được tạo ra, ngược lại các trạng thái

12

2113

12

2123

12

2133

02

2043

12

2153

02

2063

không thể tạo

và

ra các trạng thái đan rối cực đại. Như vậy, trong cùng một trạng thái kiểu Bell đối với bốn điều kiện đầu khác nhau thì có hai điều kiện đầu hệ có thể tạo ra các trạng thái kiểu Bell, trong khi hai điều kiện đầu còn lại hệ không thể tạo ra các

trạng thái kiểu Bell theo từng cặp

20

02

và

hoặc

12

21

. Khi β

càng tăng, trong một trạng thái kiểu Bell đối với bốn điều kiện đầu khác nhau thì có hai điều kiện đầu giá trị xác suất của các trạng thái tăng, trong khi đối với hai điều kiện đầu còn lại giá trị xác suất của các trạng thái lại giảm. Các trạng thái

2013

(Hình 2.20),

02

(Hình 2.21),

02

(Hình 2.22),

2143

(Hình 2.23),

và

02

2053

(Hình 2.24),

12

2163

(Hình 2.25) càng xấp xỉ bằng đơn

và

vị, nghĩa là các trạng thái kiểu Bell được tạo ra với độ chính xác cao, trong khi các trạng thái còn lại hầu như không tạo ra được các trạng thái kiểu Bell. Hơn