Trạng Thái Lượng Tử Của Qubit Ứng Với Các Điểm Trên Mặt Cầu Bloch

1

1

sp2n 2

2



22. (1.59)

1

Có thể bạn quan tâm!

• Ứng dụng lý thuyết quá trình ngẫu nhiên để nghiên cứu thăng giáng lượng tử trong các bộ nối phi tuyến kiểu Kerr - 2
• Lý Thuyết Cơ Sở Của Quá Trình Ngẫu Nhiên Và Mô Hình Kéo Lượng Tử Phi Tuyến
• Các Trạng Thái Lượng Tử Hữu Hạn Chiều
• Kéo Lượng Tử Phi Tuyến Dựa Trên Các Dao Động Tử Phi Tuyến Kerr
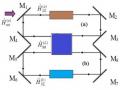
• Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Một Mode
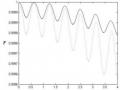
• Độ Tin Cậy Của Trạng Thái Cắt Đối Với Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Một Mode (Đường Nét Liền) Và Hai Mode (Đường Chấm

Xem toàn bộ 144 trang tài liệu này.



s



n0

n! s 

L s 1

p

Sự định nghĩa như vậy tương đương với trường hợp trong đó trạng thái

p s

được tạo ra do kết quả của sự tác dụng toán tử

e~aˆvào trạng thái chân không 0 .

Các trạng thái này thường được gọi là các trạng thái kết hợp cắt.

1.3.3. Trạng thái đan rối

1.3.3.1. Khái niệm qubit

Ngày nay, thông tin được lưu trữ, tính toán và xử lý thông qua các bit, trong đó mỗi bit chỉ có thể tồn tại ở trạng thái 0 hoặc 1. Tuy nhiên, trong thời đại ngày nay, với sự phát triển như vũ bão của khoa học kỹ thuật, sự bùng nổ của công nghệ cao đặt ra yêu cầu lượng thông tin lưu trữ và tốc độ xử lý ngày càng tăng lên nhưng kích thước của các vi mạch ngày càng nhỏ lại. Công nghệ vi mạch tiến tới các giới hạn mà vật lý cho phép. Để vượt qua khó khăn này, lý thuyết thông tin lượng tử đã ra đời. Thuật ngữ qubit hay bit lượng tử, một đơn vị của thông tin lượng tử, là một hệ lượng tử hai trạng thái được biểu diễn trong không gian Hilbert hai chiều, do Benjamin Schumacher đề xuất lần đầu tiên vào năm 1993, có dạng như sau [76]:

a 0 b 1 , (1.60)

ở đây các số phức a và b thỏa mãn điều kiện chuẩn hóa a 2 b 2 1, hai trạng

thái 0và 1lập thành một hệ cơ sở trực chuẩn. Lúc đó, chúng ta có thể biểu diễn các trạng thái này trong không gian Hilbert hai chiều dưới dạng ma trận:

,

1

00

1 0. (1.61)



1



Từ đó, trạng thái của một qubit được tham số hóa có thể được viết dưới dạng:

= cos 

2

0 eisin 

2

1 . (1.62)

Nó có thể biểu diễn bằng một điểm trên mặt cầu Bloch (Hình 1.2) tương ứng với mỗi cặp giá trị của các tham số thực và (và biến đổi từ 0 đến 2π). Kết quả là có vô số các tổ hợp tuyến tính của hai trạng thái 0và 1trên mặt cầu. Như vậy, về lý thuyết qubit có thể lưu trữ được một lượng thông tin vô cùng lớn. Hơn nữa, việc xử lý các bit trong một vi mạch của máy tính cổ điển được tiến hành trong các nhánh một cách song song với nhau. Trong khi, trong mạch logic của máy tính lượng tử, nếu các qubit rối với nhau trong cùng một trạng thái thì trạng thái của một qubit thay đổi sẽ làm trạng thái của các qubit khác thay đổi ngay lập tức. Điều này khẳng định rằng máy tính lượng tử có tốc độ xử lý thông tin nhanh hơn rất nhiều so với máy tính cổ điển.

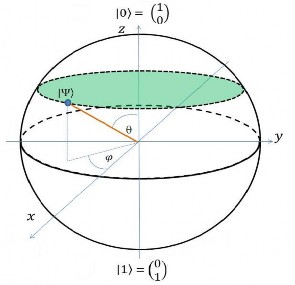
Hình 1.2: Trạng thái lượng tử của qubit ứng với các điểm trên mặt cầu Bloch

Ví dụ điển hình là để giải bài toán phân tích ra thừa số nguyên tố của một số nguyên dài hàng trăm chữ số, bằng siêu máy tính truyền thống hiện nay thì mất khoảng 14 tỷ năm, nhưng nếu sử dụng máy tính lượng tử thì bài toán này chỉ thực hiện trong khoảng vài giây [77]. Do đó, trong tương lai gần một cuộc cách mạng thực sự về công nghệ thông tin sẽ xuất hiện, khi máy tính lượng tử được tạo ra bởi nguồn tài nguyên là các qubit.

Tuy nhiên, vấn đề khó khăn đặt ra là có bao nhiêu thông tin được biểu

22

diễn bằng một qubit và bằng cách nào để thao tác trên các qubit. Về nguyên tắc, do mặt cầu Bloch có vô số điểm nên mỗi qubit sẽ lưu trữ được vô số thông tin. Nhưng khi thao tác trên mỗi qubit, theo quy luật lượng tử, chúng ta sẽ không chắc chắn tìm được giá trị nào, mà chỉ có thể tìm được một giá trị tương ứng với xác suất nào đó. Đồng thời, trạng thái của qubit cũng sẽ bị phá vỡ khi thực hiện phép đo, trạng thái của hệ chuyển sang trạng thái riêng tương ứng với trị riêng của toán tử thực hiện phép đo mà chúng ta nhận được một giá trị ngẫu nhiên với xác suất nào đó.

1.3.3.2. Trạng thái đan rối

Trạng thái đan rối (entangled state) là trạng thái của một hệ lượng tử gồm nhiều hệ con mà trạng thái lượng tử của chúng có mối quan hệ ràng buộc lẫn nhau, dù chúng cách xa nhau tới mức nào [77, 78]. Trong không gian Hilbert là tích tenxơ của các không gian Hilbert hai chiều:

H H1 H 2  ... H n , (1.63)

Trạng thái lượng tử tổng quát nhất của hệ n qubit có dạng như sau:

c

1,2,...n1

00...0

c2

01...0

 ... c n

11...1

, (1.64)

2

ở đây ci ( i = 1, 2,... 2n) là các hệ số phức thỏa mãn điều kiện chuẩn hóa:

2

n2

ci

,







i 1

 1. (1.65)

Ta gọi

,...,

lần lượt là trạng thái trong các không gian Hilbert

H1 ,

2

1

n

H 2 ,..., H n

tương ứng. Lúc đó, trạng thái lượng tử n qubit

1,2...n

gọi là trạng



,







thái phân tách được nếu nó luôn được biểu diễn dưới dạng tích tenxơ của các

trạng thái

,...,

như sau:

2





1

n

1,2,...n

...

n . (1.66)



1 2

Ngược lại, nếu trạng thái

1,2,...n

luôn được biểu diễn dưới dạng





1,2,..., n

1,2,..., n

thì nó được gọi là trạng thái đan rối của hệ n qubit.

Ta không thể xác định được trạng thái riêng của từng hệ mà chỉ có thể xác định được trạng thái chung của các hệ lượng tử đan rối với nhau. Nếu muốn xác định trạng thái riêng của một hệ con nào đó thì phải thực hiện phép đo thích hợp lên hệ con đó. Khi các hệ con không đan rối với nhau thì trạng thái của chúng là độc lập nhau nên các phép đo lên một hệ con nào đó không hề ảnh hưởng đến trạng thái của các hệ con khác. Ngược lại, khi các hệ đan rối với nhau, trạng thái của chúng không còn độc lập nữa. Do đó, mỗi sự tác động đến một hệ con thì sẽ ngay lập tức làm ảnh hưởng đến các hệ con khác của nó. Ta có thể thu được một kết quả ngẫu nhiên với xác suất xác định khi thực hiện phép đo trên một hệ con nào đó, từ kết quả này có thể xác định được trạng thái của các hệ con còn lại mà không cần thực hiện các phép đo trên chúng. Kết quả là tốc độ xử lý thông tin trên các hệ đan rối nhanh hơn rất nhiều so với các hệ không đan rối. Ngoài ra, kết quả đo được trên một hệ con cho phép ta xác định được trạng thái của các hệ con còn lại dù chúng rất xa nhau. Đây chính là nền tảng cơ bản của hiệu ứng viễn tải lượng tử.

1.3.4. Các trạng thái Bell

Các trạng thái Bell là những trạng thái đan rối đa mode đơn giản nhất. Khái niệm trạng thái này được đặt theo tên của John F. Bell bởi vì nó liên quan đến bất đẳng thức nổi tiếng của ông [79] và đã được phát triển bởi Clauser và cộng sự [80]. Do mối liên hệ của các trạng thái Bell với nghịch lý EPR nên trong trường hợp riêng hai qubit, chúng thường được gọi là cặp EPR.

Chúng tôi chỉ xét trường hợp đơn giản gồm hai trạng thái chân không và một photon trong mỗi mode và giả thiết rằng đối với mỗi mode được dán nhãn là A hoặc B, ta có 0 hoặc 1 photon, lúc đó các trạng thái Bell có thể được biểu diễn dưới dạng sau [19]:

1

 10

2 A B

1

 10

2 A B

 1 0 ,

A

A

B

B

 1 0 ,

(1.67)

0

 10

2 A B

0

 10

2 A B

 1 1 ,

A

A

B

B

 1 1 .

Các trạng thái Bell là những trạng thái hai qubit và đan rối cực đại. Mỗi phép đo cụ thể đối với một trạng thái Bell chỉ có thể xác định được thông tin về tính chẵn lẻ hoặc về pha của trạng thái mà không thể xác định được trạng thái đan rối của cả hệ.

0

A

N

B

Khái niệm của các trạng thái Bell có thể được mở rộng thành trạng thái có nhiều photon trong hệ, đó là trạng thái NOON đã được đề xuất bởi Sanders [81] bằng cách sử dụng trạng thái N thay cho trạng thái một photon 1. Các trạng thái NOON đóng một vai trò quan trọng trong thông tin lượng tử và có thể được biểu diễn như sau



NOON

 1N

2 A B

eiN0

, (1.68)

ở đây tham số kí hiệu một pha lượng tử bất kỳ.

Ngoài ra, khái niệm các trạng thái Bell cũng được mở rộng thành các trạng thái Bell tổng quát biểu diễn dưới dạng [82]:

mn

D1

1

e2ikm / D k

D

k nmod D

, (1.69)

k 0

ở đây D là một số nguyên dương lớn hơn 2.

1.3.5. Cách tính độ đan rối của một trạng thái lượng tử

Entropy là một khái niệm của vật lý thống kê được dùng cho lý thuyết thông tin lượng tử, đo lường mức độ không chắc chắn có trong trạng thái của một hệ vật lý. Có thể sử dụng entropy von Neumann để xác định độ đan rối của các trạng thái n qubit [83-85]. Trạng thái của một hệ lượng tử tổng quát có thể

được biểu diễn bởi ma trận mật độ dưới dạng

pi i i

i

, (1.70)

với i

là trạng thái của hệ có xác suất tương ứng là

pi . Tuy nhiên, khi chỉ đề

cập đến hệ lượng tử hai thành phần với trạng thái được mô tả bởi ma trận mật độ như (1.70) thì ma trận mật độ của hai hệ con A và B chính chính là các ma trận mật độ rút gọn của (1.70), là vết theo B (A) của ma trận toàn phần của hai hệ con

A và B được viết tương ứng dưới dạng [84, 85]:

B

i

A

i

Tr ,



(1.71)

B TrA i i .

Tính độ đan rối chính là phép đo mức độ vướng víu giữa các thành phần trong hệ. Phép đo này rất phức tạp đối với các trạng thái đan rối hỗn tạp. Nhưng ta lại có thể đo một cách chính xác hay ít nhất cũng có thể so sánh mức độ đan rối giữa các trạng thái cùng một họ rất dễ dàng đối với các trạng thái thuần. Giữa hai hệ con A và B không có bất kỳ sự ràng buộc nào khi các ma trận mật độ rút gọn có tính chất của một trạng thái thuần. Ngược lại, giữa hai hệ con A và B có một mối liên kết nào đó, tức là hệ AB là hệ đan rối khi các ma trận mật độ rút gọn là các ma trận mật độ của trạng thái hỗn tạp. Khi mức độ hỗn tạp của các ma trận rút gọn càng lớn thì sự tương quan giữa hai thành phần của hệ càng

mạnh. Vì vậy, độ đan rối của trạng thái thuần hai thành phần i

có thể được

xác định thông qua entropy von Neumann của một trong hai hệ con A và B:

ESS Alog ABlog

B , (1.72)



A B j 2 j j

k 2 k

k



j

ở đây A

và B

là các trị riêng tương ứng của các ma trận rút gọn

A và

B .

k

Tính độ đan rối bằng entropy von Neumann có ưu điểm này là có độ chính xác tuyệt đối dựa trên quan điểm thống kê. Tuy nhiên, việc xác định nó đòi hỏi phải chéo hóa ma trận mật độ rút gọn là rất khó cho các trạng thái bất đối xứng.

Đối với độ đan rối của hệ lượng tử tổng quát có ma trận mật độ như (1.70)

26

được định nghĩa như là đan rối trung bình của các trạng thái thuần phân ly, giảm đến mức tối thiểu trên tất cả sự phân ly của ma trận mật độ [85]:

E min pi Ei

i

. (1.73)

Đối với một cặp qubit, giá trị cực tiểu trong (1.73) có thể được biểu diễn như một hàm tường minh của ma trận mật độ . Công thức này có thể được gọi là phép biến đổi đảo spin, nó được áp dụng cho các trạng thái với một số lượng qubit tùy ý. Đối với một trạng thái thuần của một qubit đơn, đảo spin, được ký hiệu dưới dạng [86]:

*

~y

, (1.74)

ở đây *

là liên hợp phức của trạng thái , còn y

là ma trận Pauli chuyển pha

có dạng y

0

i



i.

0



Để biểu diễn một đảo spin đối với n qubit, người ta áp dụng biến đổi trên cho mỗi qubit riêng lẻ. Ma trận mật độ tổng quát của hệ hai qubit A và B có dạng

như (1.70). Lúc đó, ma trận mật độ đảo spin có dạng:

y y y y

~*, (1.75)

Mặc dù chúng ta đã giới thiệu khái niệm đảo spin chủ yếu là để áp dụng cho trạng thái hỗn tạp. Tuy nhiên, khái niệm này cũng thuận tiện trong việc tính độ đan rối của trạng thái thuần hai qubit. Khi đó công thức (1.72) có thể được

biểu diễn dưới dạng

E

EC

, (1.76)

trong đó, concurrence C được định nghĩa như sau:

C

~. (1.77)

Khi đó, độ đan rối của trạng thái này được định nghĩa như sau:

1  1 C2 

ECh, (1.78)

2 



27

ở đây

hxx log 2 x  (1x) log1 (1x) . (1.79)

Khi entropy đan rối

EC

thay đổi đơn điệu từ 0 đến 1 khi

C

tang từ 0

đến 1, do đó người ta có thể sử dụng concurrence như một phép đo độ đan rối theo đúng nghĩa của nó.

Khi concurrence thay đổi từ 0 đến 1 thì giá trị của entropy đan rối cũng thay đổi từ 0 đến 1. Entropy đan rối bằng 0 đối với trạng thái phân tách được, còn đối với

trạng thái có độ đan rối cực đại, nó có giá trị bằng 1.

Bây giờ chúng ta sử dụng đảo spin và

EC

để xây dựng các công thức

tính độ đan rối của trạng thái hỗn tạp hai qubit có ma trận mật độ :

 1 

Eh

2 

1 C 

, (1.80)

trong đó





C max0,

1 

2

2 





3 

4 , (1.81)

với i

( i  1,2,3,4 ) là các trị riêng của ma trận Hermitian:

y y y y

R ~*, (1.82)

và thỏa mãn điều kiện 1 2 3 4 .

1.4. Mô hình kéo lượng tử phi tuyến

Mô hình kéo lượng tử là nhóm các phương pháp hay những phương án vật lý có khả năng tạo ra sự chồng chập hữu hạn các trạng thái bằng cách cắt các trạng thái của hệ trong không gian Hilbert vô hạn chiều. Theo cách này, chúng thuộc một nhóm rộng hơn của các phương pháp công nghệ xử lý trạng thái lượng tử. Kéo lượng tử ở đây là trường hợp riêng của các hệ quang học, dựa trên các phương pháp quang học mà việc cắt có thể đạt được trong nhiều cách khác nhau. Khi phương pháp này sử dụng các môi trường quang học phi tuyến để thu được trạng thái hữu hạn chiều, ta sẽ gọi chúng là các kéo lượng tử phi tuyến (nonlinear quantum scissors - NQS).

1.4.1. Môi trường phi tuyến Kerr

Khi điện từ trường lan truyền trong môi trường đồng nhất và đẳng hướng,