Kéo Lượng Tử Phi Tuyến Dựa Trên Các Dao Động Tử Phi Tuyến Kerr





sẽ gây ra các kích ứng lên nguyên tử và tạo ra các phân cực vi mô, như một sự “phản ứng” lại của môi trường với tác dụng của trường điện từ. Đại lượng đặc trưng cho phản ứng của môi trường gọi là véctơ phân cực điện và kí hiệu là

r ,t . Theo điện động lực học, véctơ cảm ứng điện của môi trường D r,tsẽ

phụ thuộc vào tọa độ không gian và thời gian và được biểu diễn dưới dạng [87]:

D r,t 0 E r,t P r,t , (1.83)

ở đây

Có thể bạn quan tâm!

• Lý Thuyết Cơ Sở Của Quá Trình Ngẫu Nhiên Và Mô Hình Kéo Lượng Tử Phi Tuyến
• Các Trạng Thái Lượng Tử Hữu Hạn Chiều
• Trạng Thái Lượng Tử Của Qubit Ứng Với Các Điểm Trên Mặt Cầu Bloch
• Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Một Mode
• Độ Tin Cậy Của Trạng Thái Cắt Đối Với Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Một Mode (Đường Nét Liền) Và Hai Mode (Đường Chấm
• Độ Tin Cậy Của Trạng Thái Cắt Trong Bộ Nối Phi Tuyến Tương Tác Phi Tuyến

Xem toàn bộ 144 trang tài liệu này.

0 là độ điện thẩm của chân không. Cũng có thể đưa vào véctơ phân cực

từ tương tự như vậy. Tuy nhiên, việc đưa vào một đại lượng như vậy theo [88] sẽ không có ý nghĩa. Do đó, véctơ cảm ứng từ phụ thuộc vào tọa độ không gian và thời gian có thể được biểu diễn dưới dạng sau:

B r ,t 0 H r ,t , (1.84)

với 0

là độ từ thẩm của chân không.

E r , t và

H r ,t 

tương ứng là véctơ

cường độ điện trường và từ trường, được xác định theo các phương trình Maxwell như sau:





rotE r , t

t B

r , t ,







j r, t ,

rotH r , t

0 0 t E

r , t

(1.85)

divB

r , t



 0,

divE

r , t



r, t ,

trong đó





B r ,t

là véctơ cảm ứng từ,

j r,t 

là véctơ mật độ dòng và

r,t là mật

độ điện tích tự do. Nếu chỉ xét đối với môi trường điện môi thì

j r ,t và

r,t sẽ

bằng không. Trong trường hợp điện từ trường yếu, nghĩa là các véctơ cường độ điện trường và từ trường rất nhỏ so với trường nội nguyên tử, chúng có thể được xem như

các nhiễu loạn nhỏ lên nguyên tử. Khi đó, véctơ r ,t 

sẽ phụ thuộc tuyến tính vào

véctơ cường độ điện trường

E r , t . Tuy nhiên, đối với những trường laser mạnh có

độ lớn véctơ trường so sánh được với độ lớn các véctơ trường nội nguyên tử, véctơ

phân cực điện

r,t 

sẽ phụ thuộc phi tuyến vào véctơ cường độ điện trường

E r , t như sau [89]:

r ,t 1r ,t 22r ,t 33r ,t  ...nnr ,t , (1.86)

(1)

là độ cảm tuyến tính của môi trường, còn

( 2) ,

(3) ,...,

( n )

lần lượt là độ

cảm phi tuyến bậc 2, bậc 3,..., bậc n của môi trường.



Trong môi trường đồng nhất và đẳng hướng, luôn có sự đối xứng đối với phép nghịch đảo tọa độ không gian nên các thành phần phi tuyến bậc chẵn của môi trường bị triệt tiêu [88]. Thêm vào đó, từ độ cảm phi tuyến bậc 5 trở lên sẽ rất nhỏ so với độ cảm phi tuyến bậc 3 nên có thể bỏ qua. Khi đó, véctơ phân cực điện môi chỉ gồm các thành phần phụ thuộc tuyến tính và phi tuyến bậc 3 vào véctơ cường độ điện trường:

r ,t 1r ,t 33 r ,t

. (1.87)

133

Môi trường phi tuyến như trên được gọi là môi trường phi tuyến Kerr. Khi đó, véctơ cảm ứng điện của môi trường có thể được viết lại dưới dạng sau:

D r ,t 0r ,t r ,t  (0)r ,t r ,t , (1.88) còn biểu thức Hamiltonian của trường được viết dưới dạng:

H 1





E r , t

2

D r , t B r , t H

r , t dV



1

1

33 

1



(1.89)

E r , t 0

2 

E r , t

E r , t

B r , t

0

B r , t dV



Ta xét trường hợp đơn giản khi trường là đơn mode, còn sóng điện từ lan truyền dọc theo trục z trong khoảng từ 0 đến L. Lúc đó, thành phần điện trường và từ trường phân cực dọc tương ứng theo trục x và trục y. Với các điều kiện biên E(0, t) = E(L, t) = 0, B(0, t) = B(L, t) = 0, nghiệm của hệ phương trình Maxwell (1.85) có dạng sau [90]:

x z,t 

22

0

q t sin kz , (1.90)

 00



y z,t 

22

p t cos kz , (1.91)

k 0

ở đây k 

c

là số sóng, q(t) và p(t) là các thành phần phụ thuộc thời gian và

thỏa mãn điều kiện p t 

như sau:

d q t . Từ đó, Hamiltonian (1.89) được viết lại

dt

2

1 L 

12

34

1 2 

dz 0

xz, t 

xz, t 

y z, t  . (1.92)

0 0 

Thay các biểu thức (1.90) và (1.91) vào Hamiltonian (1.92) ta tìm được:

1 2 2 2

(1) 2 2

(3) 4 4





p q q 2 q . (1.93)

2 20 20





Ta tiến hành lượng tử hóa trường theo nguyên lý tương ứng bằng cách thay thế Hamiltonian (1.93) bằng toán tử Hamilton:

ˆ 1 2 2 2

(1) 2 2

(3) 4 4

pˆ qˆ qˆ

2qˆ ,

(1.94)

ở đây

2 20

20

qˆ 

(aˆ aˆ,



2

2

(1.95)

pˆ 1

i

(aˆ aˆ,

ở đây aˆ, aˆlần lượt là các toán tử hủy và sinh photon.

Thay biểu thức (1.95) vào biểu thức (1.94), ta thu được biểu thức của toán tử Hamilton:

ˆ1

aˆ

aˆ 1

(1)

aˆ aˆ2

(3) 22

2

aˆ aˆ4

. (1.96)

2 40 80

Bởi vì mốc để tính năng lượng là tùy ý nên có thể chọn mốc là năng lượng của chân không và coi như bằng không. Lúc đó toán tử Hamilton phải được viết dưới dạng tích chuẩn, tức là toán tử sinh bên trái và toán tử hủy bên phải. Nếu

lấy trung bình trong chân không thì các số hạng khác sẽ triệt tiêu. Khi đó, toán tử Hamilton (1.96) có thể được viết lại dưới dạng sau:

ˆ (1)

(3) 22 

(3) 22

2 2

aˆ

aˆ 





20

22

aˆ



aˆ 

42

aˆ

aˆ

. (1.97)

0

0

Từ đó có thể thấy rằng, vì tính chất phi tuyến của môi trường nên biểu thức của

toán tử Hamilton đã xuất hiện các thành phần phi tuyến (aˆ)2aˆ2. Đây chính là cơ

sở để xây dựng mô hình kéo lượng tử phi tuyến dựa trên các dao động tử phi tuyến Kerr ở phần tiếp theo.

1.4.2. Kéo lượng tử phi tuyến dựa trên các dao động tử phi tuyến Kerr

NQS là một nhóm những thiết bị quang học trong đó các phần tử phi tuyến như các dao động tử phi tuyến được sử dụng [90, 91]. Những thiết bị này cắt các trạng thái quang học trong không gian Hilbert vô hạn chiều thành các trạng thái gồm một vài n-photon được mô tả hoàn toàn trong không gian Hilbert hữu hạn chiều. Đã có một số đề xuất về các thiết bị như vậy và nói chung chúng có thể được chia thành các nhóm khác nhau theo số mode của các trạng thái thu được. Quá trình cắt được liên kết chặt chẽ với viễn tải trạng thái trong các thiết bị NQS và các hiện tượng lượng tử khác. Chẳng hạn, sự tạo thành các trạng thái đan rối cực đại hoặc sự chết và hồi sinh đan rối xuất hiện trong những điều kiện đặc biệt [92]. Người ta có thể tìm các trường hợp về NQS được sử dụng để tạo ra các trạng thái cắt một hoặc hai mode.

1.4.2.1. Kéo lượng tử phi tuyến đối với các trạng thái một mode

Trong nhóm NQS, dựa trên các phần tử quang học phi tuyến, có các thiết bị tạo ra các trạng thái Fock đơn mode hoặc đa mode. Trước hết, ta sẽ tập trung vào các hệ có thể tạo ra các trạng thái hữu hạn chiều đơn mode của trường điện từ. Trong số đó, người ta cần đề cập đến phương pháp “cắt” các toán tử trường được đề xuất trong nghiên cứu của Leoński và Tanaś [93] và được phát triển trong nghiên cứu của Leoński và các cộng sự [94].

Như đã đề cập trong phần trước, trạng thái kết hợp hữu hạn chiều có thể

tìm được bằng cách sử dụng toán tử dịch chuyển

Dˆ(,*)

tác động lên trạng thái

32

chân không, trong đó các toán tử sinh và hủy photon được định nghĩa trong không gian Hilbert hữu hạn chiều (xem các Phương trình (1.51) - (1.57)), trái với trạng thái kết hợp cắt, được định nghĩa như một hiệu ứng cắt của sự mở rộng trạng thái kết hợp Glauber trong cơ sở trạng thái n-photon (các phương trình (1.58) và (1.59)). Để tạo ra trạng thái kết hợp hữu hạn chiều, chúng ta có thể áp dụng mô hình được đề xuất bởi Leoński và Tanaś [93]. Khi biên độ và thời gian giữa các kích có giá trị phù hợp thì trường trong một buồng, kích theo chu kỳ bởi các xung cổ điển và chứa một môi trường phi tuyến Kerr, có thể tạo ra trạng thái lượng tử một photon, toán tử unita mô tả sự tiến triển của hệ được viết dưới

dạng:

U  expiT / 2nˆnˆ 1expiaˆ*aˆ, (1.98) với là hệ số phi tuyến, T biểu thị thời gian giữa các lần kích tiếp theo và nˆ aˆaˆ là toán tử số photon. Tham số là một đại lượng mô tả độ mạnh của sự kích tỷ lệ với biên độ của trường kích cổ điển từ bên ngoài. Nếu giả định rằng ban đầu hệ ở

trạng thái chân không, kích thích yếu (tức là

), kích nhiều lần và thời gian

cho mỗi lần kích đủ lâu thì có thể tạo ra trạng thái một photon với độ chính xác cao, với điều kiện là các quá trình tắt dần đủ nhỏ. Hơn nữa, đối với trường hợp này, quá trình tiến triển của hệ trở nên khép kín trong tập hợp hai trạng thái: trạng thái chân không 0và trạng thái một photon 1.

Người ta có thể thay đổi mô hình này và sau khi có những điều chỉnh thích hợp của độ lệch cộng hưởng trong hệ, phần Hamiltonian của hệ tương ứng với sự tiến triển của môi trường phi tuyến trở thành:

Hˆ1nˆnˆ  2. (1.99)

2

Sự tiến triển của hệ, với giả thiết quá trình kích là hai photon, được khép kín trong các trạng thái 0và 2và trạng thái hai photon cũng có thể được tạo ra.

Mô hình này có thể được mở rộng cho trường hợp Hamiltonian phi tuyến tỉ lệ

với

nˆnˆ z, trong đó z là một số tự nhiên tùy ý, và kích thích liên quan đến quá

trình z-photon thì trạng thái z-photon sẽ được tạo ra [95].

Ngoài ra, Kilin và Horoshko [96] đã xây dựng một Hamiltonian thích hợp để tạo ra trạng thái Fock n-photon, trong đó sự biến đổi lẫn nhau giữa trạng thái chân không và trạng thái n-photon có thể được viết dưới dạng sau:

Hˆn0

Hˆnn

n,

. (1.100)

 0 .

Ở đây, người ta đã thảo luận về một số lớp con của phép biến đổi và tập trung vào những vấn đề được xác định bởi:

eitnHˆn0

n ,

(1.101)

trong đó

tn / 2  2k

với k là một số nguyên. Khi đó, dạng của Hamiltonian

phi tuyến tạo ra các phép biến đổi này được biểu diễn như sau:

ˆ 

aˆaˆ 

aˆ2

Hn aˆ

aˆ aˆ n

aˆ 1 

n 

H.c.. (1.102)

n! 



Nếu sử dụng môi trường phi tuyến thì Hamiltonian mô tả hệ vật lý có thể thu

được bằng cách giả thiết rằng tham số thực  0 . Khi đó, trường bơm có tần số

 nằm trong quá trình (1.102) được chuyển thành trạng thái Fock n-photon có

tần số  / n đồng thời theo hai cách:

n

và n  1.

1.4.2.2. Kéo lượng tử phi tuyến đối với các trạng thái hai mode

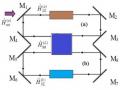
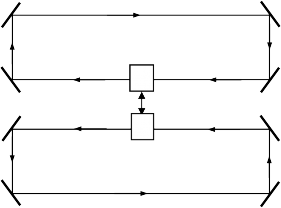
Các đề xuất đầu tiên về NQS đối với trạng thái hai mode được trình bày trong [20, 97], trong đó hệ quang học gồm bộ nối phi tuyến được điều khiển bởi trường ngoài kết hợp đã được thảo luận. Bộ phận chính của NQS bao gồm hai dao động tử phi tuyến liên kết tuyến tính, phi tuyến,…với nhau và được mô tả bởi tính phi tuyến Kerr. Sơ đồ tổng quát của kéo lượng tử phi tuyến hai mode được trình bày ở Hình 1.3.

Dạng tổng quát của Hamiltonian mô tả hệ kéo lượng tử phi tuyến có thể được viết dưới dạng:

HˆHˆ0Hˆ1,

Hˆ0aaˆ aˆ bˆbˆ,



b

a extb

Hˆ1HˆaHˆbHˆint Hˆext Hˆ ,

(1.103)

ở đây

Hˆ a

aaˆ2aˆ2

2

và Hˆb

bbˆ2bˆ2

2

lần lượt là Hamiltonian phi tuyến của

các mode a và b.

Hˆint

là Hamiltonian tương tác giữa các mode với nhau, tương

tác này có thể là tương tác tuyến tính [20], tương tác phi tuyến [98-100], hay

tương tác kiểu tham số [101],

Hˆ ext

và Hˆ ext

lần lượt là Hamiltonian tương tác

a

b

của mode a và mode b với trường ngoài. Nếu

Hˆext  0

hoặc

Hˆext  0

thì kéo

a

b

lượng tử chỉ được bơm một mode a hay b, tương ứng bởi trường ngoài. Tùy thuộc vào dạng tương tác giữa các mode với nhau và số mode được bơm bởi trường ngoài mà các trạng thái tìm được từ các bộ nối phi tuyến sẽ khác nhau.

a

Hˆext

b

Hˆext

a

b

Hˆ a



Hˆ b

Hình 1.3: Mô hình chung của kéo lượng tử phi tuyến hai mode

Ta biết rằng các trạng thái hai mode chứa một số lượng lớn photon trong không gian Hilbert vô hạn được mô tả bởi Hamiltonian (1.103) có dạng phổ biến sau:



(t)

cmn (t) m an b, (1.104)

m,n 0

trong đó

cmn (t)

là các biên độ xác suất. Để tìm được tập hợp kín của phương

trình (1.104), nghĩa là hệ khép kín trong tập hữu hạn các trạng thái n-photon, thì các điều kiện thích hợp cần được thỏa mãn. Nói chung, do sự suy biến của các

Hamiltonian

Hˆ a

và Hˆb

và nếu giả sử rằng các kích thích phải đủ yếu, tức là giá

trị của các tham số mô tả các tương tác này phải nhỏ hơn đáng kể so với các hệ số phi tuyến, thì hệ có khả năng chỉ tạo ra một số trạng thái hai mode. Chẳng

hạn khi hai mode liên kết tuyến tính với nhau [20, 97], trạng thái cắt được tạo ra của hệ chỉ khép kín trong bốn trạng thái có dạng đơn giản như sau:

t 

cut

1

n

cmn t m a b m,n0

(1.105)

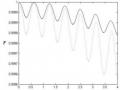
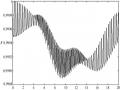
Độ chính xác của phép cắt này được xác định bằng độ tin cậy giữa các trạng thái (1.104) và (1.105). Bất kỳ độ lệch nào từ việc cắt hoàn hảo là có bậc của 10-4 đối với các tham số được chọn thích hợp, đặc biệt là tỷ lệ giữa các hệ số phi tuyến và tương tác. Tùy thuộc vào dạng tương tác giữa các mode với nhau và số mode tương tác với trường ngoài mà độ tin cậy của quá trình cắt được thực hiện bởi kéo lượng tử phi tuyến thu được các kết quả khác nhau.

1.5. Kết luận chương 1

Trong chương này, chúng tôi đã trình bày các khái niệm cơ bản và lý thuyết về các quá trình ngẫu nhiên trong quang học lượng tử. Trước hết chúng tôi trình bày các mô hình ngẫu nhiên của ánh sáng laser đơn mode, đa mode và laser với thăng giáng bơm. Tiếp theo chúng tôi trình bày lý thuyết nhiễu trắng và áp dụng cho trường hợp tuyến tính.

Các trạng thái hữu hạn chiều thường được áp dụng và thảo luận trong lý thuyết thông tin lượng tử, quang lượng tử hoặc tổng quát hơn là các mô hình kỹ thuật lượng tử. Người ta có thể tìm được nhiều phương pháp khác nhau để tạo ra các trạng thái Fock, kết hợp hữu hạn chiều hoặc đan rối trong các hệ quang học. Kéo lượng tử là thiết bị cho phép thu được các trạng thái như vậy. NQS được xây dựng với sự áp dụng của những phần tử phi tuyến. Hơn nữa, chúng có thể là nguồn cung cấp các trạng thái cắt. Các trạng thái này biểu hiện tính chất rất thú vị, chúng có thể là đối tượng của các nghiên cứu trong lĩnh vực quang học lượng tử. Tuy nhiên, kéo lượng tử có thể được áp dụng cho các mô hình quang học khác. Mô hình kéo lượng tử phi tuyến sẽ được ứng dụng để nghiên cứu sự hình thành các trạng thái có độ đan rối cao ở các chương tiếp theo.