Định Lý 1 Giả Sử Hàm F(X,y) Thỏa 3 Điều Kiện

Bài 14Cho hàm hai biến z = e

x2y 2+ ln1

. Tính vi phân cấp một dz,dz(4,3).

x 2 y 2

2

Bài 15 Cho hàm hai biến z = yln(y2+ x2) . Tính dz , dz(

, 1),

2 z

yx

4,3

Có thể bạn quan tâm!

• Toán cao cấp A2 - Trường ĐH Sư phạm Kỹ thuật TP.HCM - 20
• Ñònh Nghóa ( Số Gia Riêng Và Số Gia Toàn Phần)
• Định Lý Nếu Hàm Số Nhiều Biến Có Tất Cả Các Đạo Hàm Riêng Cấp K Miền D Thì Tồn Tại Vi Phân Đến Cấp K Của Hàm Số Trên Miền D.
• Cách Tìm Cực Trị Hàm Hai Biến Dựa Vào Định Lý Điều Kiện Cần , Định Lý Điều Kiện Đủ, Tiêu Chuẩn Sylvester Vào Việc Xét Dấu Dạng Toàn Phương,
• Cách Tìm Cho Hàm F (X, Y) Liên Tục Trên Tập Đóng Và Bị Chặn E .
• Toán cao cấp A2 - Trường ĐH Sư phạm Kỹ thuật TP.HCM - 26

Xem toàn bộ 224 trang tài liệu này.

Bài 16Cho hàm hai biến z = f(x,y). Khẳng định nào đúng? Khẳng định nào sai?

A) Nếu hàm f(x,y) khả vi tại (xo,yo) thì f(x,y) có các đạo hàm riêng tại (xo,yo).

B) Nếu hàm f(x,y) có các đạo hàm riêng liên tục trên tập mở D chứa điểm (xo,yo) thì f(x,y) khả vi tại (xo,yo).

C) Nếu hàm f(x,y) có các đạo hàm riêng tại (xo,yo) thì f(x,y) liên tục tại (xo,yo).

D) Nếu hàm f(x,y) khả vi tại (xo,yo) thì f(x,y) liên tục tại (xo,yo).

f

E) Nếu hàm f(x,y) có các đạo hàm riêng tại (xo,yo) thì f(x,y) khả vi tại (xo,yo).

x

y

F) Nếu hàm f(x,y) có các đạo hàm riêng trên D.

f ' ,

' liên tục trên tập mở D thì f(x,y) khả vi

xy(x 2 y 2 )



khi

(x, y)  (0,0) ''

Bài 17Cho hàm số

yx

vaø f '' (0,0)1.

f (x, y) 



x 2 y 2

0

khi

(x, y)  (0,0)

. Chứng minh

fxy(0,0)-1

Bài 18Một đoạn mạch gồm hai điện trở

R1và

R2mắc song song thì tổng trở R của

đoạn mạch tính bởi công thức

1  1 

1. Chứng minh rằng: R

1

R R

R R

2

R R1 R2

1 R

2 R

Bài 19 a) Chứng minh rằng hàm z= yln( x2- y2) thỏa mãn phương trình 1z x'1z 'yz

x y y 2

x

y

y

b) Chứng minh rằng nếu z = xy + x e xthì : xz ' yz' xy  z

Bài 20

a) Tính vi phân cấp hai

d 2 f (x, y) , d 2 f (2,1)

của hàm số

f (x, y) x 2 ln y  4x3 y 2 e2 x5 y

(x x )2  ( y y )2

o

o

b) Tính vi phân cấp hai d 2f (x, y, z) , d 2f (1,2,2) của hàm số

f (x, y, z) z 2 e y y 3 ln x e2 x z 3

Bài 21Với 0 bé, tập

B(xo

, yo

),(x, y) R 2:

gọi là

f

lân cận (xo, yo)

hay gọi tắt là lân cận (xo, yo) . Nếu hàm

z f (x, y) có các đạo hàm

x

riêng f ' ,

' liên tục trong

B(xo

, yo

),thì

y

L(x, y) 

f (xo

, yo

) + f ' (x

, yo

)(x xo

) + f ' (x

, yo

)( y xo ) 

f (x, y)

(x, y) B(xo

, yo

),

x

y

o

o

Công thức xấp xỉ này gọi là xấp xỉ tuyến tính (linear approximation) của

f (x, y)

trong lân cận

(xo, yo) . Với hàm ba biến f (x, y, z) , chúng ta cũng có công thức xấp xỉ tương tự .

a) Tìm xấp xỉ tuyến tính hàm số

f (0.2,0.5).

b) Tìm xấp xỉ tuyến tính hàm số

f (2.2,0.8,0.7).

f (x, y)  6 e3y 2 x trong lân cận điểm

f (x, y) xy 2ln z trong lân cận điểm

(0,0) và ước tính

(2,1,1) và ước tính

c) Ước tính

f (1.8,1.5)

biết

f (2,1)  1 , f ' (2,1)  2 , f ' (2,1)  1.

x y

§4. ĐẠO HÀM HÀM HỢP- ĐẠO HÀM HÀM ẨN

Sau khi học xong bài này, bạn có thể:

Hiểu khái niệm hàm hợp và tính được đạo hàm hàm hợp.

Hiểu khái niệm hàm ẩn và tính được đạo hàm hàm ẩn.

Biết ứng dụng đạo hàm hàm hợp, đạo hàm hàm ẩn trong tính gần đúng.

1. Đạo hàm và vi phân hàm hợp

1.1-Ñònh nghóa

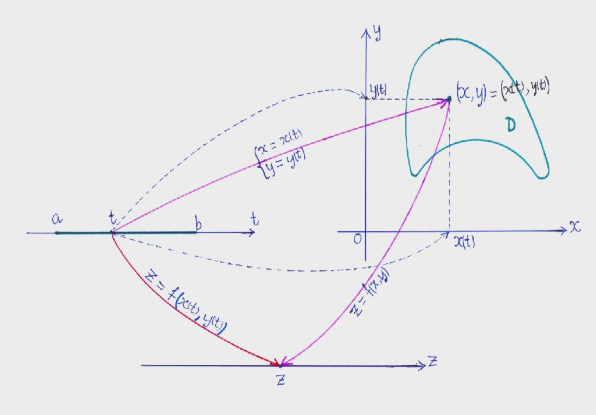
Nếu hàm hai biến

z f (x, y)

xác định trên

D 2và các hàm

x x(t), y y(t)

xác định

trên khoảng

(a, b)  thỏa x(t), y(t)D

t  (a, b) , thì

z f x(t), y(t)

là hàm số xác

định trên khoảng (a, b) và gọi là hàm hợp.

1.2- Định lý 1 (Đạo hàm hàm hợp-Quy tắc xích)

Giả sử t  (a, b) thì x(t), y(t)D .

Nếu hàm

z f (x, y)

khả vi theo biến

(x, y) D 2và các hàm

x x(t), y y(t)

khả vi

theo biến t  (a, b) thì hàm hợp

z f x(t), y(t)khả vi theo biến t  (a, b) và ta có

df f . dx f . dy  dz

dt x dt y dt dt

Ví dụ 5.26 Tính

dfbiết

dt

f (x, y) x 2 e y x ,

x(t) t 2 , y(t)  sin t .

Cách 1

Giải

df f . dx f . dy  (2xe y  1)2t x 2 e y cos t

dt x dt y dt

 (2t 2 esin t  1)2t t 4 esin t cos t  4t 3esin t  2t t 4 esin t cos t

Cách 2Thay

x(t) t 2 , y(t)  sin t

vào

f (x, y) x 2 e y x

được

f x(t), y(t)= t 4 esin t t 2 .

df= 4t 3esint t 4 esint cos t  2t

dt

Ví dụ 5.27(Đạo hàm hàm hợp-Quy tắc xích)

Cho hàm sản xuất dạng Cobb-Douglas : Q(K , L)  20.L23K 13

( Q là sản lượng-đơn vị là1000 sản phẩm; K là vốn-đơn vị là $1,000,000 ; L là lực lượng lao động-đơn vị là 1000 người )

a) Tìm sản lượng biên tế của vốn QKvà sản lượng biên tế của lực lượng lao động QLôû

mức

K  5

và

L  3 .

b) Giả sử K  5, L  3 , lực lượng lao động tăng 60 người/năm, vốn giảm $150,000 /năm. Áp

dụng quy tắc đạo hàm hàm hợp, ước tính tốc độ thay đổi của sản lượng.

Giải

a) Sản lượng biên tế của vốn : Q=

2

20 L 3

K 

3 K 

1

Sản lượng biên tế của lực lượng lao động: Q= 40K3

L 3 L 

Sản lượng biên tế của vốn ở mức

K  5

3

2

và



L  3 :

Q (5,3) =

20 3 

4,74 (1000 sản phẩm)

K 

3  5 

Sản lượng biên tế của lực lượng lao động QLở mức

1

K  5

và

L  3 :

Q (5,3)

= 40 5 

3

 15,81

(1000 sản phẩm)

L 

3  3 

b) Lực lượng lao động tăng 60 người/năm:

dL  0,06

dt

Vốn giảm $150,000 /năm:

dK 0,15

dt

Ước tính tốc độ thay đổi sản lượng

dQ Q dK + Q dL

 4,74  (0,15) +15,81 0,06 = 0,2376 (1000 sản phẩm/năm)

dt K dt L dt

1.3-Ñònh nghóa

Nếu hàm

z f (u)

xác định trên tập

I  vaø hàm hai biến

u u(x, y)

xác định trên tập

D 2thỏa

u(x, y) I

(x, y) D

thì

z f u(x, y)

là hàm số xác định trên tập D và

gọi là hàm hợp.

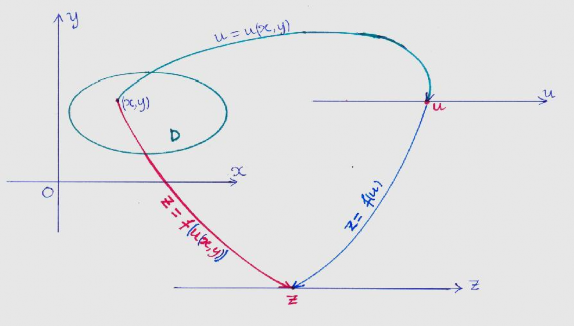
1.4 -Định lý 2

Giả sử (x, y) D

thì u u(x, y) I

và hàm

z f (u) xác định trên tập I .

Nếu hàm u u(x, y) khả vi theo biến (x, y) D và hàm z 

f (u) khả vi theo biến u I

thì hàm

hợp

z f u(x, y)có các đạo hàm riêng theo các biến x, y và ta có

f (x, y) df . u (x, y) ; f (x, y) df . u (x, y)

x

1.5-Ñònh nghóa

du x

y du y

Nếu hàm

z f (u, v)

xác định trên tập

D' và các hàm hai biến

u u(x, y) , v v(x, y)

xác

định trên tập

D 2 thỏa

(u, v) D'

(x, y) D

thì

z f u(x, y), v(x, y)

là hàm số xác

định trên tập D và gọi là hàm hợp.

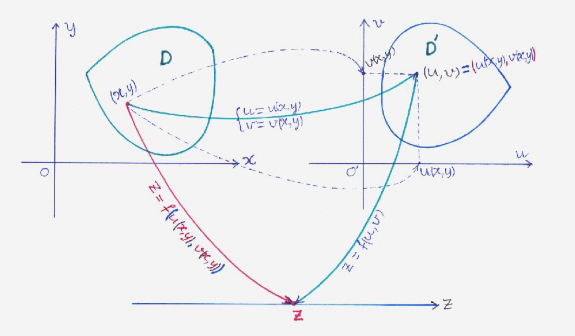
1.6 -Định lý 3

Nếu hàm

f (u, v)

khả vi theo biến (u,v) và các hàm u = u(x,y) , v = v(x,y) khả vi theo biến

(x, y) thì hàm hợp

f u(x, y), v(x, y)

có các đạo hàm riêng theo biến x, y và ta có:

f (x, y) f (u, v). u (x, y) f (u, v). v (x, y)

f 

u

v f 

x

u x

v x

x 

x

x u 

f

f u

f v

f u

v f 

 (x, y) 

(u, v).

(x, y) 

(u, v).

(x, y)





y

u y

v y

y 

y

y v 



u

x

v 

x 





Ma trận u

v 

gọi là ma trận Jacobi của u,v đối với x,y.







y y 

u v

Ký hiệu

D(u, v) x

D(x, y) u

y

v

x = J gọi là định thức Jacobi của u,v đối với x,y.

y

2- Đạo hàm và vi phân hàm ẩn

2.1.Định nghĩa

a) Cho phương trình

F x, y  0 , trong đó

F x, y 

xác định trên miền mở

D 2. Nếu tồn

tại khoảng a, bđể mọi

x  (a,b) tồn tại duy nhất

y y xsao cho

F x, y x 0 thì ta nói

F x, y  0 xác định hàm ẩn y theo x . Khi đó

y y x

gọi là hàm ẩn xác định bởi phương

trình

F x, y  0 .

b) Tương tự :

z z(x, y) là hàm ẩn hai biến xác định bởi phương trình

F x, y, z  0 ;

u u(x, y, z)

là hàm ẩn ba biến xác định bởi phương trình

F (x, y, z,u)  0 ;

u u(x, y) và

v v(x, y) hai biến xác định bởi hệ phương trình

F (x, y,u, v)  0



G(x, y,u, v)  0

;….

Các định lý sau đây chỉ ra khi nào tồn tại hàm ẩn và cách tính đạo hàm hàm ẩn.

2.2- Định lý 1 Giả sử hàm F(x,y) thỏa 3 điều kiện

i) F(x,y) liên tục trong lân cận (xo , yo ) và F(x0,y0) = 0.

ii) F(x,y) có các đạo hàm riêng

f , f

liên tục trong lân cận (x , y ) .



iii) F (x 0 , y0 ) 0

y

x y o o

Khi đó phương trình F(x,y) = 0 xác định một hàm ẩn y = y(x) trong lân cận điểm x0thỏa

yoy(xo) . Hơn nữa hàm y = y(x) khả vi và liên tục trong lân cận điểm x0và ta có:

y ' dy 

F

F

F



'

x =x

dx F '

y

y

Ví dụ 5.28Tính đạo hàm

xy x sin y  0 (*)

y'(x) ,

y ' (1 )

của hàm ẩn

Giải

y y(x)

xác định bởi:

Thay

x  1 vào phương trình ta được:

y  sin y  0

Giải phương trình ta được nghiệm duy nhất y .

Cách 1Đặt F (x, y) =

xy x sin y 

F

F '

sin y y

x

F ' y  sin y ,

' x x cos y y'(x) =x=

F

'

y

y

x x cos y

y'(1) =

sin 

1  1cos



2

Cách 2Lấy vi phân toàn phần hai vế của đẳng thức (*) ta được

( y  sin y)dx  (x x cos y)dy  0

dy 

dx

sin y y x x cos y

(1)

Mà

y'(x) =

dy (2)

dx

Từ (1) và (2) suy ra:

y'(x)

 sin y y ,

x x cos y

y'(1) =

sin

1  1cos



2

Ví dụ 5.29Cho

y y xlà hàm ẩn xác định bởi phương trình

Giải

x  sin xy y3 exy . Tính

y '0.

F x, y x  sin xy y3 exy .



1y.cos xy y.exy

y ' x  .

x.cos xy  3y2 x.exy

Khi

x  0 , ta có

y 0 1. Vậy

y '01

3

2.2-Định lý 2 Giả sử hàm F(x,y,z) thỏa 3 điều kiện:

i) F(x,y,z) liên tục trong lân cận (xo , yo , zo ) và F (x0,y0,z0) = 0.

ii) F(x,y,z) có các đạo hàm riêng liên tục trong lân cận điểm (x0,y0,z0)

z

iii) F' (x 0

, y0

, z 0

)  0

Khi đó phương trình F(x,y,z) = 0 xác định một hàm ẩn 2 biến

z z(x, y)

trong một lân cận nào

đó của điểm (x0,y0) thỏa

zo z(xo, yo) . Hàm



F

z z(x, y) liên tục, có các đạo hàm riêng

- F

F

liên tục trong lân cận (x0,y0) và:

z x'



F

;

x

z

x F '

z

z 

y

y 

F

z

- F' '

y

F

z

Ví dụ 5.30Tính đạo hàm riêng hàm ẩn z = z(x, y) xác định bởi phươnh trình :

y2ez +z3 –3 y + 6x – x2 = 0 (*)

Cách 1Đặt

F

F (x, y, z)

Giải

F

z

= y2ez +z3 –3 y + 6x – x2

F

z

x

'  6  2x ’,

'  2 ye z  3 ,

' y 2 e z  3z 2

z

y

x

Suy ra:

' 

6  2x

y 2 e z  3z 2

 2x  6 ,

y 2 e z  3z 2

' 

2 ye z  3

y 2 e z  3z 2

 3  2 ye z

y 2 e z  3z 2

y

Cách 2Lấy vi phân toàn phần hai vế của đẳng thức (*) ta được

(6  2x)dx  (2 ye z  3)dy  ( y 2 e z  3z 2 )dz  0

( y 2 e z  3z 2 )dz  (2x  6)dx  (3  2 ye z )dy

dz 

2x  6 dx 

y 2 e z  3z 2

3  2 ye z

y 2 e z  3z 2 dy

(1)

Mặt khác dz  z'dx  z'dy (2)

x

Từ (1) và (2) suy ra:

y

x

z ' 

2x  6 ,

y 2 e z  3z 2

z ' 

3  2 ye z

y 2 e z  3z 2

y

Ví dụ 5.31Tính đạo hàm riêng hàm ẩn z = z(x, y) xác định bởi phương trình

ez +z3 – y3 +6x2 = 2x3

Giải

Phương trình tương đương với: ez+z3– y3+6x2- 2x3= 0 (*)

Lấy vi phân toàn phần hai vế của đẳng thức (*) ta được (ez+3z2)dz –3y2dy +(12x – 6x2)dx = 0

(ez +3z2)dz = (6x2 -12x)dx +3y2dy

dz (6x 2 12x) dx 

ez 3z 2

3y 2

ez 3z 2

dy (1)

Mặt khác dz  z'dx  z'dy (2)

x

Từ (1) và (2) suy ra:

y

z ' = (6x 2 12x) , z' = 3y 2

x ez 3z 2 y ez 3z 2

Ví dụ 5.32Cho hàm ẩn

z z x, y xác định từ phương trình

x2z y2z2 2xy3z  0 ,

vớixlà hàm khả vi trên R . Tính z 'x x, y , z 'y x, y .

Giải

2 2 2

Đặt F x, y, z x2z y2z2 2xy3z .

3

F 'x x, y, z  2xz  2 y z ,

F 'y x, y, z  2 y'y z  6xy z ,

F 'zx, y, z x2 2z'y2z2 2xy3

Suy ra

z 'x

x, y F 'x

F 'z

F '

2xz  2 y3 z 

x2 2z.'y2z2 2xy3,

2 y.'y2z2 6xy2z

z 'y

x, y y

F 'z

x2 2z'y2z2 2xy3.

BÀI TẬP

Bài 1Tính đạo hàm các hàm hợp

a) Tính du với u e x2 y , x  sin t, y t 3

dt

c) Tính

z ,

u

z với

v

z x 2 ln y, x u , y  3u  2v

v

b) Tính dfvới fx, yx y

dt

và

x lnt



y sint

d) Tính dzvới z  arcsinx y, x  3t, y  4t 3

dt

e) Tính

df, fvà

f nếu

fx; ylnexeyvới y 1x3x

dx x y

f f

3

x2 y2

2

Bài 2Tính 1;2

x

Bài 3Đạo hàm ẩn

và

1;2nếu fx; y

y

et dt

2x

a) Tính

dy, d 2 y

nếu x-y + arctgy = 0 b) Tính

dy, d 2 y

nếu x+y= ex-y

dx

c) Tính y1

dx2

và

dx

y1nếu x2+2xy+y2-4x+2y-2= 0 và y(1) = 1.

dx2

d) Tính

e) Tính

y'(x) nếu

y'(x) nếu

x3 y xy3  1

xey yex exy  0

Bài 4Tính cac đạo hàm riêng

z, z

của hàm ẩn z z(x, y) trong các trường hợp sau:

a) z lnx zxy 0

2

x y

c) y4ez +z3 – y2 – 8x3 –3x2 +1= 0

d) x2e3z +z3 – x2 + 6y = y2

b) zez xex yey

e) 3yz 2 e4 x cos 4z  3y 2  4

Bài 5Cho hàm số u xz . Tính u , u

biết rằng z là hàm ẩn của x, y được xác định bởi

y z x y

phương trình : zez xex yey .

y 2z 2

Bài 6

a) Chứng minh hàm ẩn

z zx, yxác định bởi phương trình z 22

x

thỏa mãn

x2 z1 z 1

x y y z

b) Chứng minh rằng hàm z yfx 2 y 2thỏa mãn

1 z1 zz 2

x x

Bài 7 Cho u = f(v,w) với v = x – y , w = y – x. Chứng minh

y y y 2

u u

x y

 0 .

Bài 8 Tính

D(u, v) ,

D(x, y)

D(x, y)

D(u, v)

với u = 2x – 3y ,v = - x + 2y.

Xem tất cả 224 trang.