Toán cao cấp A2 - Trường ĐH Sư phạm Kỹ thuật TP.HCM

§1. HÀM NHIỀU BIẾN

Sau khi học xong bài này, bạn có thể:

Hiểu khái niệm hàm số hai biến, ba biến, n biến.

Hiểu khái niệm miền xác định, miền giá trị hàm số.

Biết cách tìm miền xác định hàm số theo nghĩa toán học và theo nghĩa ứng dụng thực tiễn.

Hiểu khái niệm đồ thị hàm nhiều biến và vẽ được đồ thị hàm hai biến một số trường hợp đơn giản-Các đồ thị có liên liên quan đến đường và mặt bậc hai.

Hiểu khái niệm đường mức, mặt mức và ứng dụng vào thực tế.

1. Các ví dụ mở đầu Ví dụ 5.3

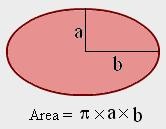
a) Một hình elip có hai bán trục lần lượt

a, b thì diện tích tính bởi công thức

S ab . Đại lượng S xác định duy nhất (phụ thuộc) vào hai đại lượng độc lập

a, b.

b) Hình quạt tròn có bán r , góc ở tâmthì diện tích tính bởi công thức

S 1 r 2.

Đại lượng S xác định duy nhất (phụ thuộc) vào hai đại lượng độc lập r,.

Độ dài cung tròn tương ứng tính bởi công thức L r. Đại lượng L xác định

duy nhất (phụ thuộc) vào hai đại lượng độc lập r,.

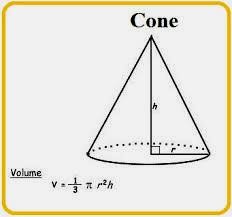
c) Khối nón (hình nón) có bán kính đáy r , chiều cao h thì thể tích tính bởi công thức V 1r 2h . Đại lượng V xác định duy nhất (phụ thuộc) vào hai đại lượng

độc lập

r, h.

d) Khối trụ (hình trụ) có bán kính đáy r , chiều cao h thì thể tích tính bởi công

thức V r 2h . Đại lượng V xác định duy nhất (phụ thuộc) vào hai đại lượng

độc lập

r, h.

Diện tích toàn phần tính bởi công thức

S  2r 2 2rh . Đại lượng

S xác định duy nhất (phụ thuộc) vào hai đại lượng độc lập r, h.

e) Một người có cân nặng

w(kg) , chiều cao

h(cm)

thì diện tích toàn phần cơ thể

S (m 2 )

được tính xấp xỉ cong thức

S S (w, h) =

0.0072w0.425h0.725. Đại lượng S

xác định duy nhất (phụ thuộc) vào hai đại lượng độc lập

w, h.

Mỗi đại lượng S , L hoặc V ở trên xác định duy nhất (phụ thuộc) vào hai đại độc lập, chúng được gọi là hàm số hai biến.

Ví dụ 5.4

a) Hai khối lượng bởi công thức

m1, m2cách nhau một khoảng r thì lực hấp dẫn giữa chúng tính

F Gm1m2

r 2

, với G là hằng số hấp dẫn

Đại lượng F xác định duy nhất (phụ thuộc) vào ba đại lượng độc lập m1, m2, r .

b) Một đoạn mạch gồm ba điện trở đoạn mạch tính bởi công thức

R 

R1 , R2 , R3

R1 R2 R3

mắc song song thì điện trở R của

R1 R2 R1 R3 R2 R3

Đại lượng R xác định duy nhất (phụ thuộc) vào ba đại lượng độc lập

R1 , R2 , R3 .

c) Một người có tuổi là A (năm), cân nặng

w(kg) , chiều cao

h(cm)

thì mức tiêu

hao năng lượng cơ bản hàng ngày B (kilo calo) tính xấp xỉ bởi công thức

Bm (w, h, A)  66.47  13.75w  5.00h  6.77 A

B f (w, h, A)  655.10  9.60w  1.85h  4.68A

(đối với nam) (đối với nữ)

Đại lượng

Bm (w, h, A) , B f (w, h, A)

xác định duy nhất (phụ thuộc) vào ba đại lượng

độc lập w, h, A .

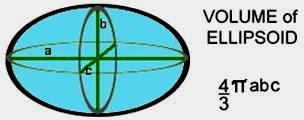
d) Thể tích khối ellipsoid có ba bán trục

a, b, c tính bởi công thức

V 4abc . Đại

lượng V xác định duy nhất (phụ thuộc) vào ba đại lượng độc lập a, b, c.

Các đại lượng

F , R , Bm , B f

hoặc V ở trên xác định duy nhất (phụ thuộc) vào ba đại

độc lập, chúng được gọi là hàm số ba biến.

2. Định nghĩa hàm nhiều biến

Cho tập

D R 2. Một quy luật, gọi tên là f , mà mỗi cặp số thực

(x, y) D

cho ta một số thực f (x, y) , gọi là một hàm số hai biến số và gọi tắt là hàm hai biến xác định trên D . Tập D gọi là tập xác định (domain) của hàm số. Nói cách khác, hàm hai biến là quy luật mà đầu vào là cặp số thực và đầu ra là một

số thực. Tập f (D) f (x, y) : (x, y) Dgọi là tập giá trị hàm số.

Cho tập D R 3. Một quy luật, gọi tên là f , mà mỗi bộ ba số thực

(x, y, z) D

cho ta một số thực f (x, y, z) , gọi là một hàm số ba biến số và gọi tắt

là hàm ba biến xác định trên D . Tập D gọi là tập xác định (domain) của hàm số. Nói cách khác, hàm ba biến là quy luật mà đầu vào là bộ ba số thực và đầu

ra là một số thực. Tập f (D) f (x, y, z) : (x, yz) Dgọi là tập giá trị hàm số.

Tương tự ta có khái niệm hàm bốn biến, hàm năm biến, …, hàm n biến. Nói cách khác, hàm n biến là quy luật mà một đại lượng (số) xác định duy nhất (phụ thuộc) vào n đại lượng (số) độc lập.

Ví dụ 5.5

a) f (x, y) xe 2 y y 2 y sin x

là hàm số theo hai biến

x, y có tập xác định là 2.

y x 2

b) g(x, y) là hàm số theo hai biến

x, y

có tập xác định là

D (x, y) R 2 : y x 2 

c) z 

f x, y  ln x y 

là hàm số theo hai biến

x, y

có tập xác định là

D (x, y) 2: x y .

d) f (r, s) 

ln r

là hàm số theo hai biến

r, s

có tập xác định là

D (r, s) R 2 :1 r  0 

e) f (x, y, z) ze 2 y yx 2 x sin z

là hàm số theo ba biến

x, y, z có tập xác định là 3.

f) u 

f x, y, z 

1x2 y2 z2

là hàm số theo ba biến

x, y, z có tập xác định là

r P

D (x, y, z) 3: x 2 y 2 z 2  14

g) Q(r, P, L,V ) là hàm số theo bốn biến

8Lv

r, P, L, v

có tập xác định là

D (r, P, L, v) R 4 : Lv  0 

Chú ý về miền xác định hàm soá

i) Về mặt toán học: Trong định nghĩa trên, chúng ta cho trước tập hợp D rồi mới xác định quy luật f của hàm số nên miền xác định hàm số đã biết trước. Nếu hàm số được cho dưới dạng biểu thức (tức là cho biết quy luật f của hàm số trước) thì miền xác định hàm số là tập tất cả các giá trị của biến sao cho biểu thức có nghĩa.

ii) Về mặt ứng dụng: Miền xác định hàm số là tập tất cả các giá trị của biến sao cho biến và hàm có ý nghĩa trong kinh tế, kỹ thuật, đời sống,…Trong trường hợp này, chúng ta cần có kiến thức về vấn đề (hay lĩnh vực) mà ta ứng dụng khi tìm tập xác định hàm số.

Ví dụ 5.6Chẳng hạn, với hàm số

Bm (w, h, A)  66.47  13.75w  5.00h  6.77 A

trong ví

dụ 2c thì tập xác định theo nghĩa toán học là 3, nhưng về mặt ứng dụng thì chúng

ta cần xét các bộ ba giá trị

(w, h, A)

có ý nghĩa trong đời sống. Chẳng hạn, nếu lấy

giá trị A  160 là vô lý vì hiện nay trên thế giới không ai sống đến 160 tuổi cả.

3. Đồ thị hàm nhiều biến

Cho hàm số

z f (x, y)

xác định trên tập D . Ứng với mỗi điểm

(x, y) D , ta xác

định tương ứng điểm x, y, f (x, y)trong không gian. Khi điểm

(x, y)

di động trên

toàn bộ tập D thì điểm x, y, f (x, y)di động trên một mặt cong (mặt phẳng được xem là mặt cong có độ cong bàng 0). Mặt cong này gọi là đồ thị hàm số

z f (x, y)

trên tập D .

Tổng quát, nếu hàm số w f (x1, x2

,..., xn) xác định trong tập D R thì tập hợp

G (x , x ,..., x , w) : (x , x

n 1 2

,..., xn

) R nn+1 gọi là đồ thị hàm số

w f (x1, x2,..., xn) trên tập D . Tuy nhiên, chúng ta chỉ biểu diễn hình học được

đồ thị hàm một biến và hàm hai biến.

Ví dụ 5.7

Đồ thị hàm số

z x 2



y 2

b) Đồ thị hàm số

z 

y 2

x 2

Có thể bạn quan tâm!

Xem toàn bộ 224 trang tài liệu này.

4. Đường mức mặt mức

4.1. Đường mức

Cho hàm số

z f (x, y) xác định trên tập D R2và

c f (D) . Đường bao gồm tất cả

các điểm (x, y) thỏa f (x, y) c

gọi là đường mức của hàm số

z f (x, y) ứng với mức c .

Ví dụ 5.8Xét hàm số

z x2  2 y2

trên

D (x, y) R2 : 4 x  4,4 y  4

có đồ thị

và đường mức là các đường elip đồng tâm O như hình vẽ.

Ví dụ 5.9Giả sử (x, y) (Kinh độ, vĩ độ) của một điểm trên mặt đất hoặc mặt nước

và T (x, y) là nhiệt độ trung bình trong một ngày cụ thể tại điểm (x, y) . Khi đó, tập tất

cả các điểm

(x, y)

mà

T (x, y) To

(với To

thuộc tập giá trị nhiệt độ tồn tại thực tế) là đường

mức và gọi là đường đẳng nhiệt ứng với To.

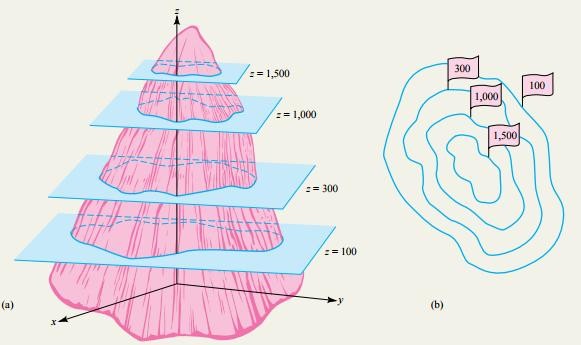
Ví dụ 5.10Áp dụng khái niệm đường mức trong việc lập đọc bản đồ địa hình, người ta lấy một mặt phẳng ngang làm chuẩn (thường là mặt nước biển) và hàm số xác định tương ứng mỗi điểm trong mặt phẳng với độ cao (hay độ sâu) đòa hình tại điểm đó. Tập các điểm có cùng độ cao tạo thành một đường mức. Sử dụng họ các đường mức cùng với đơn vị để chỉ rõ độ cao của một số đường thích hợp và đơn vị chênh lệch độ cao giữa hai đường mức kề nhau, người ta lập bản đồ địa hình.

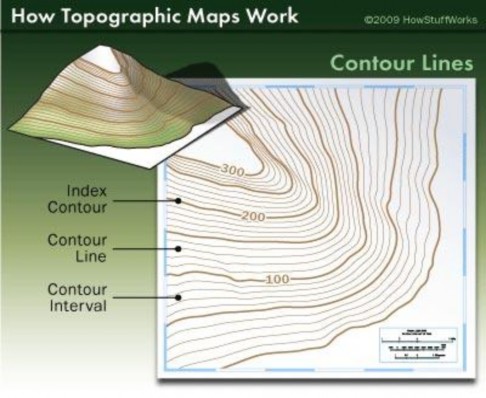
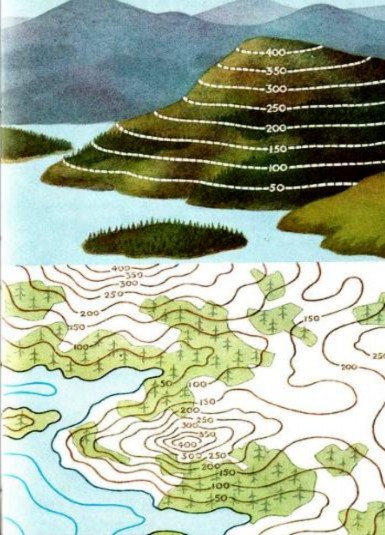
4.2. Mặt mức

Cho hàm số

w f (x, y, z) xác định trên tập

D R3

và

c f (D) . Mặt bao gồm tất cả

các điểm mức c .

(x, y, z)

thỏa

f (x, y, z) c

gọi là mặt mức của hàm số

w f (x, y, z) ứng với

Ví dụ 5.11

Giả sử

(x, y, z) (Kinh độ, vĩ độ,cao độ) của một điểm trong không gian và

P(x, y, z)

là áp suất tại điểm

(x, y, z)

ở một thời điểm to

cố định. Khi đó, tập tất cả các điểm

(x, y, z)

mà

P(x, y, z) Po

(với

Pothuộc tập giá trị áp suất tồn tại thực tế) là mặt mức và gọi

là mặt đẳng áp ứng với Po.

Tương tự, tập các điểm trong không gian có nhiệt độ bằng nhau cùng thuộc một mặt phẳng gọi là mặt đẳng nhiệt.