/ Trong Các Trường Hợp Sau Đây, Hãy Xác Định Tham Số M Để Véctơ X Là Tổ

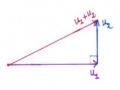
a) Để chứng minh  trực giao với

u1và u2. Ta có

Giải

W , chỉ cần chứng minh

u3trực giao với

u1 , u3  1  1  0  0 , u2 , u3  0  1  1  0

Vậy u3trực giao với u1và u2

Có thể bạn quan tâm!

Xem toàn bộ 224 trang tài liệu này.

b) Ta có

nên  trực giao với W .

w  nên w k1u1 k2 u2 k1 (1,1,0) k2 (0,1,1)  (k1 , k1 k2 , k2 )

u W 

nên u k3u3 k3 (1,1,1)  (k3 ,k3 , k3 )

Do đó,

w u v

 (k1 k3 , k1 k2 k3 , k2 k3 )  (6,1,7)

k1

k3  6

k1  2



k





k2

k3

k3

 1 

 3

 4

2

 7



3

Suy ra, w  (2,5,3) và u  (4,4,4) .

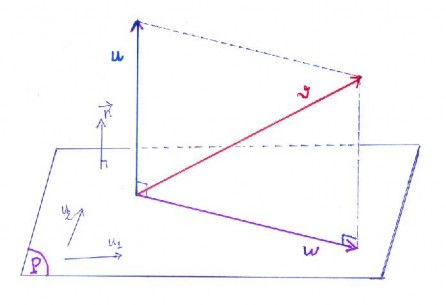
Ý nghĩaGọi (P) là mặt phẳng có cặp vectơ chỉ phương u1 (1,1,0), u2 (0,1,1) thì



u3  (1,1,1) n là vectơ pháp tuyến của (P) . Như vậy, vectơ v được phân tích thành

tổng của vectơ w song song mặt phẳng

(P)

và vectô u vuông góc mặt phẳng

(P) .

Với cách làm tương tự như trên, khi cho trước phương mặt phẳng (P) , chúng ta phân



tích được (một cách duy nhất) lực F bất kỳ thành tổng hai lực, một lực

w song song

mặt phẳng

(P)

và lực

u vuông góc mặt phẳng

(P) . Phép phân tích này áp dụng rất



nhiều trong vật lý, kỹ thuật, công nghệ điều khiển, …. 

Trong phần tiếp theo, chúng ta sẽ tổng quát phép phân tích trên cho một không gian Euclide bất kỳ.

5.4.Phép chiếu trực giao (Orthogonal projection)

5.4.1. Định lý 3.11 Cho  là không gian con của không gian Euclide  và

B u1, u2,..., unlà cơ sở trực giao của .

i) Tập = v : v, w  0, w  là một không gian con của .

ii) Với v , đặt

p  v, u1 u

 .... 

 v, u n u

và u v p

Khi đó:

 u1 , u1 

 u n , u m 

u trực giao  và v p u

với

p , u 

v p

v w

với mọi

w,

w p

Vectô p gọi là hình chiếu trực giao của v lên , ký hiệu

prW v

hay

hchW v ; vectơ u

gọi là hình chiếu trực giao của v lên , ký hiệu

pr v hay hch v .



w w

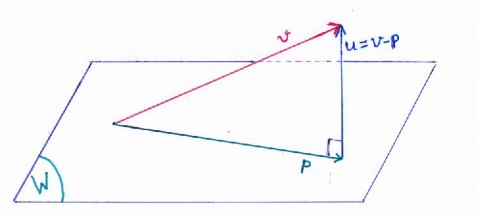
a) Với mọi v1 , v2

, với mọi

Chứng minh

w và với mọi

k .

k1v1 v2 , w =

k1 v1 , w v2 , w 

k1 .0  0

(vì v1 , v2

)

= 0

Suy ra

(k v v ) . Vậy là không gian con của .

1 1 2

b)Vì p là tổ hợp tuyến tính các vectơ trong cơ sở B của  nên p .

Để chứng minh u trực giao  , chỉ cần chứng minh u trực giao với B . Ta có

u, u1 v p, u1 v, u1 p, u1 

= v, u

-  v, u1 

u , u

 v, u 2 

1 2

u , u

 .... 

 v, u n 

1 n

u , u 

1  u

, u1 

 u 2

, u 2 

 u n

, u n 

1 1

Tương tự

v, u1 - v, u1 = 0

u, u2  0 , …, u, un  0

Suy ra, u trực giao với B . Do đó, u trực giao  hay u .

Vậy v p u

với

p , u .

Với mọi w  thì rõ ràng (v p)  ( p w) . Áp dụng định lý Pitago ta được

v w 2 

(v p)  ( p w) 2 

v p 2 

p w 2 

v p 2 , w p

Suy ra,

v p 

v w

với mọi

w và

w p ª

Nhận xét

i) Nếu 1, 2là hai không gian con hữu hạn chiều của không gian Euclide  và

1 2 thì

v - pr v 

v - pr v .

ii) Nếu v  thì p v .

5.4.2. Xấp xỉ hàm sốù

Cho

v -không gian Euclide vô hạn chiều. Nếu xây dựng được dãy các không gian

con của  có số chiều hữu hạn và tăng dần

1 2 ….n …

thì rõ ràng

v - pr v

dần về 0 khi n tăng. Khi đó, nếu n đủ lớn thì

hoặc

v  pr v

hoặc v  prWv

Phép xấp xỉ này thường được áp dụng cho không gian không gian các hàm liên tục

như

Ca, b,C(),

C(a, b) , D(a, b) , D (), .… nên được gọi là xấp xỉ hàm số. Dãy các

không gian con thường được chọn là n= Pn[x] .

Ví dụ 3.41 Trong =C()- không gian hàm số thực liên tục trên  xét tích vô hướng

ÑN 1

< f (x) ,

g(x) > f (x)g(x)dx

1

với mọi

f (x) ,

g(x) C()

Gọi  là không gian con của =C() sinh bởi cơ sở trực giao B =

2 x

{v1 1, v2 2x, v3 6x  2} và v e C(). Tìm hình chiếu p của v trên không gian con .

 e x ,1 

p  1,1 1 

 e x ,2x 

 2x,2x 

2x 

Giải

 e x ,6x 2  2 

 6x 2 - 2,6x 2 - 2 

(6x 2 - 2)

e x dx

= 1 1 

1dx

1

e x .2xdx

12x 

4x 2 dx

1

e x .(6x 2  2)dx

1(6x 2  2)

(6x 2  2)2 dx

1

= e 5 (2e  5)(6x 2  2) 8

Khi đó v e x

e 5 (2e  5)(6x 2  2) . 

Ví dụ 3.42 Xấp xỉ Fourier (Fourier Approximation)

Trong C[,] - không gian các hàm số liên tục trên [,], xét tích vô hướng



< f (x) , g(x) > = f (x)g(x)dx



với mọi

f (x) ,

g(x) C[,]

Trong ví dụ 3.37, chúng ta chứng minh

An 1, sin x, cos x, sin 2x, cos 2x,..., sin(nx), cos(nx)là cơ sở trực giao của không gian con

Fn 

1, sin x, cos x, sin 2x, cos 2x,..., sin(nx), cos(nx)

. Rõ ràng, các không gian con hữu

hạn chiều Fn

là dãy tăng

F1 F2  ... Fn  ...

Do đó, nếu

f n(x) là hình chiếu của f (x) C[,] trên Fn

thì

f n (x) f (x)

dần về 0.

Ta có

f (x) = 

f (x),1 1 

f (x), cosx cos x 

f (x), sinx sin x 

f (x), cos2x 

cos 2x

n  1,1 

 cos x, cosx 

 sin x, sinx 

 cos 2x, cos2x 

+ f (x), sin2x sin 2x  .... 

f (x), cosnx 

cos nx 

f (x), sinnx sin nx = pr f

 sin 2x, sin2x 

Bây giờ, dễ dàng tính được



 cos nx, cosnx 

 sin nx, sinnx Fn

 1,1 

1dx  2





1  cos 2kx

 cos kx, cos kx cos2kxdx 

dx ,

k  1,2,3,...

2

 sin kx, sin kx 





sin 2 kxdx 

1  cos 2kx

dx ,

k  1,2,3,...

Đặt



2 

f (x),1  1 

2

ao 

 1,1 

1 f (x)dx



f (x), coskx  1

ak  sin kx, coskx cos kx 

f (x) cos kxdx



với

k  1,2,3,...

f (x),sinkx  1

Suy ra

bk  sin kx,sinkx sin kx 

f (x) sin kxdx



với

k  1,2,3,...

f n (x) =

ao + a1 cos x 

b1 sin x a2 cos 2x b2 sin 2x  .... an cos nx bn sin nx

f (x)

Hàm số

f n (x) gọi là xấp xỉ Fourier thứ n của hàm

f (x) . 

Lưu yù Nếu f (x) C[,] thì

f n(x) hội tụ về

f (x)

x  (,) . Tức là

f (x) = ao + a1 cos x b1 sin x a2 cos 2x b2 sin 2x  .... an cos nx bn sin nx  ... ,

x  (,)

Vế phải đẳng thức này gọi là chuỗi Fourier của hàm

BÀI TẬP

f (x) .

3.1/ Trong tập R2= (x,y): x , y, xét phép cộng và phép nhân như sau:

u = (x1, y1) 2; v = (x2, y2) 2

- Phép cộng “+”: u + v = (x1 + x2, y1 + y2)

- Phép nhân “.”: u = (x1, y1); 

Tập 2với phép cộng và phép nhân như trên có là không gian véctơ trên  không? Tại sao?

3.2/ Trong tập 2= (x,y): x , y, xét phép cộng và phép nhân như sau:

u = (x1, y1) 2; v = (x2, y2) 2

- Phép cộng “+”: u + v = (x1 x2, y1 y2)

- Phép nhân “.”: u = (x1, y1); 

Tập 2với phép cộng và phép nhân như trên có là không gian véctơ trên  không? Tại sao?

3.3/ Trong tập = (x,y,z): x , y, z  và x + y + z = 0, xét phép cộng và phép nhân như sau: u = (x1, x2, x3) V; v = (y1, y2, y3) .

- Phép cộng “+”: u + v = (x1+ y1, x2 + y2,x3 +y3)

- Phép nhân “.”: u = (x1, x2, x3); 

a) Tập  với phép cộng và phép nhân như trên có là không gian véctơ trên 

không? Tại sao?

b) Tập  có là không gian con của 3không ? Tại sao?

3.4/ Cho  là tập tất cả các chuỗi số thực hội tụ. Trong  xét phép cộng và phép nhân như sau:

- Phép cộng “+”: Phép cộng hai chuỗi số.

- Phép nhân “.”: Phép nhân một số thực với một chuỗi số.

Tập  với phép cộng và phép nhân như trên có là không gian véctơ trên  không? Tại sao?

3.5/ Trong các trường hợp sau đây, xét xem  có là không gian con của nkhông (n3, và nlà kgvt trên ).

a) W = (x1, x2, ......, xn) Rn : x1 0

b) W = (x1, x2, ...., xn) Rn: x1+2x2= x3 

3.6/ Cho  là không gian các ma trận vuông cấp n trên . Tập con nào sau đây là không gian con của ?

a) Tập tất cả các ma trận đường chéo.

b) Tập tất cả các ma trận đối xứng ( tức là AT= A).

3.7/ Trong các trường hợp sau đây, hãy xác định tham số m để véctơ x là tổ hợp tuyến tính của các véctơ u, v, w.

a) Trong R3 : u = (3, 4, 2) , v = (6, 8, 7) , w = ( 5, 6, m) , x = (1,3, 5) .

b) Trong R3 : u = (4, 4, 3) , v = (7, 2, 1) , w = ( 4, 1, 6) , x = ( 5, 9, m) .

c) Trong R3 : u = (1, -3, 2) , v = (2, -1, 1) , w = ( 3, -4, 3) , x = (1, m, 5).

d) Trong R4 : u = (1, 2,-3, 2), v = (4, 1, 3, -2) , w = (16, 9, 1, -3), x =(m, 4,-7,7).

e) Trong P2[t]: u(t) =2+2t+4t2, v(t)=1-t-3t2, w(t) = 3 + 3t+ 6t2, x(t) = m +9t +5t2.

3.8/ Cho x, y, z là ba véctơ độc lập tuyến tính trong không gian véctơ . Xét tính độc lập tuyến tính , phụ thuộc tuyến tính cuả các tập véctơ sau:

a) S = u = x + y -2 z , v = x - y -z , w = x + z 

b) S = u = x + y , v = y + z, w =z + x

c) S = u = x, v = x+ y, w = x + y + mz , biện luận theo m.

d) S = u = x + y - 3z, v = x+ 3y - z, w = y + mz , biện luận theo m.

3.9/ Xét tính độc lập tuyến tính , phụ thuộc tuyến tính của các tập véctơ sau: a) M = (1, 2, 3) , ( 3, 6, 7)trong 3.

b) M = ( 2, -3, m), ( 3,-2, 5), ( 1, -4, 3) trong 3.

c) M = ( 1, 0, 1, 1) , (0, 1, 1, 1) , (1, 1, 0, 1), ( 1, 1, 1, m)trong 4.

d) M = x2 + x + 1, 2x2 + x + 2, 3x2 + mx + 3trong 2[x] = 2[x].

3.10/ Tìm hạng của các hệ véctơ sau:

a) u1 = (1, 2, -1), u2 = ( 0, 1, 1) , u3 =( 2, 3, -3).

b) u1 = (1, 2, -1 ), u2 =( 1, 1, -2), u3 =( 0, 3, 3), u4 =( 2, 3, -3).

c) u1 = (1, -1, 0, 0 ), u2 =( 0, 1, -1, 0), u3 =( 0, 0, 1, -1), u4 =( -1, 0, 0, 1).

3.11/ Trong không gian 4cho các tập:

W1 = (x1, x2 , x3 , x4) R4 : x1 + x2 = 2x3 , x1 - x2 = 2x4 

W2 = (x1, x2 , x3 , x4) R4 : x1 = x2 = x3 

a) Chứng minh rằng W1, W2là các không gian con của 4.

b) Tìm một cơ sở của W1, một cơ sở của W2.

3.12/ Trong không gian 4, cho các véctơ: u1= (1,-1, -4, 0 ), u2=( 1, 1, 2, 4),

u3=(2,1, 1, 6), u4=( 2, -1, -5, 2). Đặt W = < u1, u2, u3, u4>.

a) Tìm hạng của hệ véctơ u1, u2, u3, u4

b) u1, u2, u3, u4độc lập tuyến tính hay phụ thuộc tuyến tính?

c) Tìm một cơ sở và số chiều của W.

d) Véctơ u = (6, 2, 0, 16) có thuộc W không? Nếu u thuộc W thì tìm tọa độ véctơ u đối với cơ sở vừa tìm được ở câu (c).

e) Hãy bổ sung vào cơ sở ở câu (c) để được một cơ sở một cơ sở của 4.

3.13/ Trong 3, cho tập M = u1= (1, 1, 2) , u2= (-1, 0, 1), u3=(1, 2, m). Với giá trị nào của m thì M là tập sinh của 3.

3.14/ Trong các tập véctơ sau , xét xem tập nào là cơ sở của 3.

a) M = u1 =(1, 2, 1) , u2 = (1, 7, 5)

b) M = u1 =(1, 2, 3), u2 = ( 1, 1, 1) , u3 =( 3,4,2) , u4 = ( 7, 2,1)

c) M = u1 =(1, 2, 3), u2 =(2, 3, 4) , u3 =( 3, 4, 5) 

d) M = u1 = (1, 1, 2) , u2 =( 1,2,1), u3 =(3 , 2, 2) 

3.15/ Trong 3, các phát biểu sau đây, phát biểu nào đúng?

a) M là tập độc lập tuyến tính, M có ba véctơ thì M là cơ sở của3.

b) M là tập sinh của 3, M có ba véctơ thì M là cơ sở của 3.

c) M là tập sinh của 3thì M có ít nhất ba phần tử.

d) M là tập độc lập tuyến tính thì M không thể có quá ba phần tử.

e) M là tập phụ thuộc tuyến tính thì M có ít nhất ba phần tử.

f) M có ít hơn ba phần tử thì M độc lập tuyến tính.

g) M có bốn phần tử thì M là tập sinh của 3.

3.16/ Trong mỗi trường hợp sau đây, hãy xác định tham số m để : a) M = ( 0, 1, 1), ( 1, 2, 1), (1, 3, m)sinh ra 3.

b) M = ( m, 3, 1), (0, m-1, 2), ( 0, 0, m+1)là cơ sở của 3.

3.17/ Cho B = u1, u2, u3là một cơ sở của không gian véctơ  trên  và đặt E = v1= mu1+ u2+3u3, v2= mu1-2u2+ u3, v3= u1- u2+ u3

a) Xác định m để E là cơ sở của .

b) Tìm ma trận chuyển cơ sở từ B sang E.

3.18/ Trong 4cho tập B = (1,2, -1, -2), (2,3, 0, -1), (1, 2, 1, 4),(1,3, -1, 0).

Chứng minh rằng B là cơ sở của 4và tìm tọa độ của véctơ x = (7,14, -1,2) đối với cơ sở này.

3.19/ Trong R3 cho hai hệ véctơ B = u1 =(1,2,3), u2 =(1,1,2), u3 =(1,1,1)E = v1 = (2,1,-1) , v2 = (3,2,-5), v3 =(1, -1, m) .