2
2
2
2
a b + a . b
= a . b
(công thức Lagrange)
a ( b c ) = ( a . c ) b - ( a . b ) c (công thức Gibbs)
( a b ) c = ( a . c ) b - ( b . c ) a
( công thức Gibbs)
6.1.3-Tọa độ của vectơ tích Nếu
a = (a1,a2,a3) , b = (b1,b2,b3) thì
a
a a a a a
i j k
a b
= 2
3 ; 3
1 ; 1
2 = a1 a 2 a 3
b 2
b3 b3
b1 b1
b 2
b1 b2 b3
6.2 . Tích hỗn hợp vectơ
6.2 .1- Ñònh nghóa Tích hỗn hợp của 3 vectơ a , b , c ; ký hiệu ( a , b , c ); là một số
ÑN
thực được xác định như sau: ( a , b , c ) ( a b ) c .
6.2 .2- Tính chất của tích tổng hợp
( a , b , c )
= Thể tích hình hộp dựng nên bởi 3 vectơ a , b , c
α ( a , b ,
c ) = ( α a , b ,
c ) = ( a , α b ,
c ) =( a ,
b , α c )
( a + a' , b ,
c ) = ( a , b ,
c ) + ( a' , b , c )
( a , b , c ) = - ( b , a , c ) = - ( a , c , hợp
đổi dấu.
b ) Hoán vị 2 trong 3 vectơ thì tích hỗn
( a , b ,
c ) = ( c , a ,
b ) = ( b , c ,
a ) Tính chất hoán vị vòng tròn.
( a , b , c ) = 0 a , b , c đồng phẳng .
6.2.3. Biểu thức giải tích của tích hỗn hợp
a (a1, a 2 , a 3 )
a1 a 2 a 3
Nếu b (b1, b2 , b3 )
c (c1, c2 , c3 )
thì ( a , b ,
c ) = b1 b2 b3
c1 c2c3
Hệ quả Trong không gian Oxyz cho 4 điểm A, B, C, D. Khi đó thể tích tứ diện ABCD là
1
VABCD =
6
AB, AC, AD
§7. CÁC MẶT BẬC HAI CHÍNH TẮC
7.1 Mặt Elipxôit (elipsoid)
x 2 a 2 | | y2 b2 | z 2 c2 | = 1 | Khi a = b = c = R thì mặt Elipxôit trở thành mặt cầu bán kính R. | |
Dưới đây là các công trình kiến trúc có hình | ||||||
dạng Elipsoid.
|
Có thể bạn quan tâm!
-
Độ Dài Vectơ (Muđun Vectơ, Chuẩn Vectơ) -
/ Trong Các Trường Hợp Sau Đây, Hãy Xác Định Tham Số M Để Véctơ X Là Tổ Hợp Tuyến Tính Của Các Véctơ U, V, W. -
/ Một Vật Có Khối Lượng M Được Đặt Ở Cuối Lò Xo Và Kéo Theo Hướng Thẳng Đứng Về Phía Dưới Rồi Thả Ra, Thì Hệ Vật Và Lò Xo Sẽ Bắt Đầu -
Thuật Toán Chéo Hóa Ma Trận Cho A Là Ma Trận Vuông Cấp N. -
Thuật Toán Chéo Hóa Trực Giao Ma Trận Đối Xứng Thực -
Đưa Dạng Toàn Phương Về Dạng Chính Tắc Bằng Phương Pháp Lagrange
Xem toàn bộ 224 trang tài liệu này.
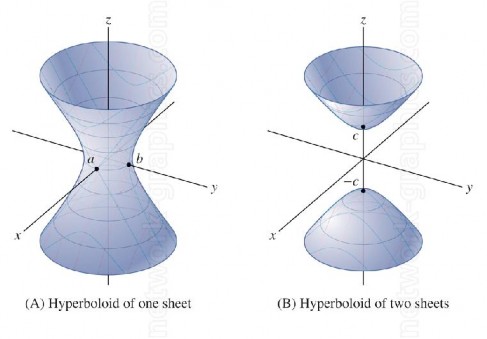
7.2- Mặt Hyperboloit một tầng
Phương trình (H) :
x 2 y2 z 2 = 1
a 2 b2 c2
Tháp giải nhiệt lò điện hạt nhân
Khi
a b
ta được hyperbol tròn xoay và
các ứng thực tế thường có dạng này.
Hình bên phải là tháp giải nhiệt (làm mát) của nhà máy điện hạt nhân và công trình kiến trúc có dạng hyperboloit tròn xoay một tầng. Ưu điểm cấu trúc này là có thể tự sinh ra dòng không khí đi vào bên dưới thoát ra bên trên với công suất lớn mà không cần sử dụng sử dụng thiết bị hút hoặc đẩy (công trình phải đủ cao lớn) nhờ đó giảm năng lượng vận hành hệ thống; một ưu điểm nữa là nó có tính thẩm mỹ cao và phù hợp với thị hiếu thẫm mỹ hầu hết mọi người. Tuy nhiên, do các công trình phải đủ cao lớn nên dẫn đến chi phí xây xựng ban đầu các tháp này khá lớn.
7.3- Maët Hyperboloit hai taàng
Phöông trình (H): x 2 y2 z 2
= -1
a 2 b2 c2
7.4. Mặt Paraboloit –Eliptic
Phương trình (P) : x 2 y2 = z
a 2 b2
Khi a = b ta có mặt Parabol tròn xoay và các ứng thực tế thường có dạng này.
7.5. Mặt Paraboloit – Hyperbolic
( mặt yên ngựa)
Phương trình (P):
x 2 y2
a 2 b2
= z
7.6-Mặt nón
2 2
Phương trình: z 2 x y .
a 2 b2
Khi a = b ta có mặt nón tròn.
Bên phải là hình vẽ mặt nón trong không gian 0xyz.
Đây là mặt nón dưới góc nhìn thuần toán học.
Hình ảnh chiếc nón lá thật quen thuộc và thân thương đối với người Việt Nam. Nón lá dùng để che nắng, che mưa, làm quạt, đạo cụ, làm đẹp, làm thơ, tỏ tình, se duyên,….Có lẽ ban đầu ông cha ta tạo ra chiếc nón lá chỉ để che nắng, che mưa, làm quạt cho những người nông dân một nắng hai sương trên các cách đồng hay những người buôn gánh bán bưng và nhờ hình dạng, cấu trúc, nguyên liệu mà nón lá làm thật tốt các công năng này. Ngày nay, khi vai trò che nắng, che mưa giảm dần thì nón lá lại xuất hiện (ngày càng nhiều) trong những không gian trang trọng, ấm cúng, đậm đà bản sắc Việt, làm lắng động tâm hồn không chỉ người Việt Nam mà cả du khách Quốc tế; nhờ đó nón lá tiếp tục mang lại thật nhiều hạnh phúc cho tất cả mọi người. Hình như ông cha ta chẳng sử dụng kiến thức toán học cao siêu gì mà chỉ bằng trực giác di truyền bẩm sinh cộng với các trãi nghiệm, kinh nghiệm để tạo ra sản phẩm này. Ngẫm nghĩ, đối với người học toán hay làm toán, việc suy nghĩ tìm tòi ứng dụng những gì đã học để mang lại hạnh phúc cho bản thân và mọi người cũng quan trọng không kém việc tạo ra kiến thức mới hay học thật nhiều kiến thức cho bản thân mà không biết ứng dụng. Chúng ta cần học và hành như thế nào để có nhiều sản phẩm tương tự như bên dưới đây mang tên nhà thế kế Việt ?!
Gợi nhớ tới hình ảnh nón lá Việt Nam từ 
chiếc đèn của nhà thiết kế Federico Churba
7.7-Mặt truTrong mặt phẳng
(P)
cho đường cong (C). Một đường thẳng (d) song
song với trục vuông góc với (P) , di động và dựa vào đường cong (C) sẽ quét thành
một mặt gọi là mặt trụ. Đường cong (C) gọi là đường chuẩn, đường thẳng (d) gọi là đường sinh.
Nếu đường cong (C) là đường tròn, elip , hyperbol, parabol ..… thì mặt trụ được gọi tên tương ứng lần lượt là mặt trụ tròn , mặt trụ elip , mặt trụ hyperbol , mặt trụ parabol….
Thông thường, mặt phẳng
(P)
được chọn là một trong các mặt phẳng tọa độ để thuận
tiện cho việc thiết lập các phương trình biểu diễn các mặt trụ.
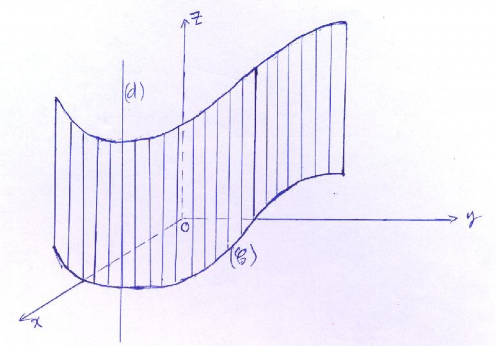
Mặt trụ với đường sinh song song trục Oz
Mặt trụ elip, mặt trụ parabol, mặt trụ hyperbol