Độ Dài Vectơ (Muđun Vectơ, Chuẩn Vectơ)

ii) x + z = (x1+ z1 , x2 +z2,…, xn +zn)

<x+z,y>= 1 (x1+ z1) y1+2( x2 +z2)y2 +…. n (xn +zn) yn

= (1x1 y1 + 2x2 y2 + .….+ nxn yn)+( 1z1 y1 + 2z2 y2 + .….+ nzn yn)

= <x,y>+ <z,y>

iii) < k x,y>= 1 k x1 y1 + 2 k x2 y2 + .….+ n k xn yn

= k (1x1 y1 + 2x2 y2 + .….+ nxn yn) = k <x,y>iv) <x,x>1x1 x1 + 2x2 x2 + .….+ nxn xn

= 1 x 2 + 2 x 2 + .….+ n x 2  0

1 2 n

<x,x>= 0 1 x 2 + 2 x 2 + .….+ n x 2

1 2 n



2 x 2 = .….= 2

x1 x2  .... xn  0

x  (0,0,...,0)  0 

Minh họa ý nghĩa trong kinh teá

Một loại sản phẩm sản xuất từ bốn loại nguyên liệu I, II, III, IV với giá mỗi đơn vị

nguyên liệu lần lượt là

x1 , x2 , x3 , x4

và lượng nguyên liệu cần để sản xuất mỗi sản

phẩm lần lượt là y1, y2, y3, y4; véctơ x  (x1, x2 , x3, x4) là véctơ đơn giá và

y  ( y1, y2, y3, y4) là véctơ nguyên liệu. Khi đó

Chi phí nguyên liệu để sản xuất mỗi sản phẩm biểu diễn bởi tích vô hướng Euclide

x, y x1 y1 x2 y2 x3 y3 x4 y4

Khi giá nguyên liệu I tăng 10%, nguyên liệu II tăng 12%, nguyên liệu III giảm 10%, nguyên liệu loại IV tăng 5% thì chi phí nguyên liệu để sản xuất mỗi sản phẩm biểu diễn bởi tích vô hướng

x, y  1,10x1 y1  1,12x2 y2  0,9x3 y3  1,05x4 y4

Ví dụ 3.32

a)  =

Pn [x] , 

f (x)

= ao + a1x +…+ anxn, g(x) = bo + b1x+ …+bnxn

ÑN

Pn[x] . Khi đó

< f (x) , g(x) > ao bo + a1 b1 +…+ an bn

là một tích vô hướng trên

Euclide trong n+1.

Pn[x] . Tích vô hướng này tương ứng với tích vô hướng

b)  =

Pn [x] , 

f (x)

= ao + a1x +…+ anxn,

g(x)

ÑN b

= bo + b1x + …+bnxn

Pn[x] . Khi đó

< f (x) ,

g(x) > f (x)g(x)dx

là một tích vô hướng trên Pn[x] .(kiểm chứng dễ dàng thỏa 4 tính chất trong định nghĩa tích vô hướng)

c)  = C[a, b] và 

f (x) ,

g(x) C[a, b] . Khi đó

ÑN b

< f (x) ,

g(x) > f (x)g(x)dx

là một tích vô hướng trên C[a, b] .(kiểm chứng dễ dàng thỏa 4 tính chất trong định nghĩa tích vô hướng)

d) Một tích vô hướng quan trọng trên không gian C[,] được ứng dụng nhiều trong kỹ thuật điện, điện tử, điện tử viễn thông là



 Chú ý

< f (x) ,

g(x) > = f (x)g(x)dx 



a) Trên cùng một không gian vectơ có thể có nhiều tích vô hướng khác nhau.

b) Khi cho không gian Euclide nmà không nói rõ tích vô hướng nào, thì ta xem như tích vô hướng được xét là tích vô hướng Euclide.

5.1.2-Tính chất Cho  là không gian Euclide và u, v, w ; k ,. Ta có

i) u, v w = u, v + u, w 

ii) u, kv = k u, v ;

iii)  0V , v = 0

u, kv =k u, v 

iv) Không gian con của một không gian Euclide cũng là không gian Euclide.

5.2.Độ dài vectơ (muđun vectơ, chuẩn vectơ)

5.2.1. Ñònh nghóa Cho không gian Euclide  và vectô u, v .

i) Chuẩn hay độ dài vectô u , ký hiệu u , là một số không âm xác định như sau

ÑN

u u, u 

ii) Khoảng cách giữa hai vectơ u và v , ký hiệu d (u, v) , là độ dài của (u v)

d (u, v) =

u v

iii) Vectô u gọi là vectô đôn vò nếu u = 1

iv) Góc giữa hai vectơ u và v là góc(0 ) thỏa

u, v 

= u v cos

Ví dụ 3.33 Xét tích vô hướng Euclide trong nvà

x  (x1 , x 2 ,..., x n ) , y  (y1 , y 2 ,..., y n ) 

x, x 

x 2x 2 ... x 2

1 2

Độ dài vectơ x : x =

Vectô x là vectơ đơn vị khi: x 2x 2 ... x 2= 1

1 2 n

(x y ) 2  (x y ) 2  ...  (x y ) 2

1 1

2 2

n n

Khoảng cách giữa hai vectơ x , y là:

d (x, y) 

x y =

Góc giữa hai vectơ x , y là góc: cos=

x1 y1 x2 y2  ... xn yn

x 2 x 2  ... x 2 . y 2 y 2  ... y 2

1 2

n 1 2



Ví dụ 3.34 Trong C() – không gian các hàm số thực liên tục trên , xét tích vô hướng

< f (x) ,

g(x) > f (x)g(x)dx

với mọi f (x) ,

g(x)

C()

Tích vô hướng của x , e x

: x, e x xe x dx  1

x 2dx 0

e 2x dx 0

e 2 1

Độ dài hai vectơ x , e x: x 

= 1,

e 2  1

ex =

x . e x

Góc giữa hai vectơ x , e xlà góc: cos=

x, e x 

5.2.2. Tính chất Cho không gian Euclide  và vectô u, v ; k . Khi đóù:

i) u  0 ; u = 0 u  0V .

ii) ku k . u

iii) u, v 

u . v

(Bất đẳng thức Cauchy – Schwarz)

Dấu “ = “ xảy ra khi u và v phụ thuộc tuyến tính (cùng phương)

iv) u  v  u  v (Bất đẳng thức tam giác).

Dấu “ = “ xảy ra khi u và v cùng chiều ( u kv hay v ku

5.3. Trực giao - Trực chuẩn 5.3.1-Định nghĩa

với

k  0)

Cho không gian Euclide  và u, v  ;  A, B .

i) Hai vectô u và v gọi là trực giao nhau, ký hiệu u v , nếu

u, v = 0

ii) Vectô v và tập A gọi là trực giao nhau, ký hiệu v A hoặc A v , nếu

u, v 

= 0,  u  A

iii) Hai tập A và B gọi là trực giao nhau, ký hiệu

<u,v> = 0, u A

A B , nếu và v B

iv) A gọi là tập trực giao nếu:  u, u' A mà u u’ thì < u,u’> = 0

v) A gọi là tập trực chuẩn nếu A là tập trực giao và u = 1,  u  A .

Ví dụ 3.35 Xét tích vô hướng Euclide:

a) Trong không gian Euclide 3 , hai vectô nhau.

u  (1,2,1)

và

v  (3,3,3) trực giao

b) Trong không gian Euclide 3, tập A = = (a , a , a ) , = (b , b

, a ) và

a 1 2 3 b

a2 a3 a3 a1 a1 a2 

1 2 3



v = 

2

b3 b3

b1 b1



b2 

= [ a , b ] trực giao nhau.

c) Trong không gian Euclide 3, {i  (1,0,0), j  (0,1,0), k  (0,0,1)} là tập trực giao.

d) Trong không gian Euclide 4, cho các tập

A  {(1,0,1,0), (1,0,1,0)}

và

B  {(0,1,0,2), (0,2,0,1)}. Dễ thấy mỗi tập A, B là tập trực giao và tập A trực giao

tập B . 

5.3.2-Tính chất

i) Nếu A là tập trực giao và 0vA thì A là tập độc lập tuyến tính.

ii) Nếu A là tập trực chuẩn thì A độc lập tuyến tính.

iii) Nếu A = u1, u 2,....., u mlà tập trực giao thì

u1  u 2  ...  u m

2  u1 2 

u 2 2  ...  u m

2 ( Định lý Pitago mở rộng )

Các cạnh góc vuông:

u1 , u 2 ,....., u m

Cạnh huyền: u1 u 2 ...  u m

Vậy, bình phương cạnh huyền bằng tổng bình phương các cạnh góc vuông.

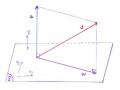
Minh họa hình học cho m = 3

Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Bình phương đường chéo hình hộp chữ nhật bằng tổng bình phương của ba kích thước.