a) Chứng minh B là cơ sở của 3. Xác định m để E là cơ sở của 3.
B E
b) Tìm ma trận chuyển cơ sở từ B sang E . Cho [v] = , tìm v, [v] .
c) Cho [x]E = , [y]E = , tìm véctơ x, [3x + 2y]E , [x]B .
B E
d) Cho [v] = , tìm v, [v] .
3.20/ Trong không gian 3, cho B =v1 =(1,0,1), v2 =(1,2,2), v3 =(0,-1,-1).
E =u1 =(1,0,-1), u2 =(1,1,1), u3 =(-1,2,2)
a) Chứng minh B, E là các cở sở của 3.
b) Tìm ma trận chuyển cơ sở từ B sang E . Cho u =(1, 2, 3) , tìm [u]B, [u]E.
B E
c) Tìm ma trận chuyển cơ sở từ E sang B . Cho [v] = , tìm v, [v] .
3.21/ Trong không gian P2[x] các đa thức thực bậc 2, cho B là cơ sở chính tắc của P2[x] và E =v1= 1 + 3x, v2= x + 2x2, v3= 1 + x + x2.
a) Chứng minh E là cơ sở P2[x].
b) Tìm ma trận chuyển cơ sở từ B sang E .
E B
c) Cho [v] = , tìm v, [v] .
3.22/ Cho B = u1, u2, u3là một cơ sở của -không gian vec tơ và các véctơ v1,
1
1
2
v2, v3có tọa độ đối với cơ sở B lần lượt là: [v]B= 1, [v]B= 2, [v]B= 2
1
3
1
a) Chứng minh E = v1, v2, v3là cơ sở của R3. Tìm v1, v2, v3theo u1, u2, u3.
b) Tìm ma rận chuyển cơ sở từ E sang B .
3.23/ Xét hệ phương trình tuyến tính thuần nhất
a11x1 a12 x2 ... a1n xn 0
a11a22 ........a1n
x1
0
a x a
x .. a
x 0
a a ........a
x 0
21 1
22 2
2n n
(*)
21 22
2n
2
AX = 0
......................
a
x
m1 1
am2 x2
amn xn 0
am1am2 ......amn xn
0
A X0
Mỗi nghiệm của hệ phương trình (*) là một vectơ trong Rnvà dễõ dàng chứng minh được tập tất cả các nghiệm của hệ (*) là một không gian con của Rn.
Trong mỗi trường hợp sau , hãy tìm một cơ sở và số chiều của không gian nghiệm của hệ phương trình:
x1 3x2
x3 0
x1 2x2 3 x3 0
a) 4x 2x
3x 0
b) 2x 3x 4x 0
1 2 3 1 2 3
5x1 x2 2x3 0 4x1 5x2 6x3 0
x1 3x2 4x3 x4 0
1 2 4
3
2x x 2x 2x 0
2 3 1 6
c) 1 2 3 4
d) AX = 0 với A =
3x1 2x2 2x3 x4 0
2 5 1 6
x1 4x2 6x3 3x4 0
3 1 7 9
3.24/ Gọi là tập hợp tất cả các hàm số thực f(x), liên tục, dương trên đoạn
a, a. Ta định nghĩa phép cộng và phép nhân như sau : f,g , .
ÑN
Phép toán cộng “+” : (f+g)(x) f(x) g(x), x[-a,a] (nhân hàm f(x) với hàm g(x))
ÑN
Phép toán nhân “.” : (f)(x) [f(x)] , x[a,b] (lũy thừahàm số f(x) )
a) Chứng minh tập với phép cộng và phép nhân như trên là một không gian vectơ trên trường .
b) Tập hợp tất cả các hàm chẵn trong không gian ở câu (a) có là không gian con của không ? Tại sao?
3.25/ Trong không gian n, cho các véctơ:
u1 = (a11, a12, ......, a1n)
u2 = (a21, a22, ......, a2n)
a11
a21
.......
am1 : b
………………………………………….
Đặt A
a12
a22
.......
1
am2 :b2
um = (am1, am2, ......, amn)
...
...
.......
.....
. ...
và u = ( b1, b2,...., bn)
a1n
a2n
.......
amn :bn
A
Chứng minh rằng: u là tổ hợp tuyến tính của u1, u2,.........,umr(A) = r( A ).
3.26/ Gọi W là không gian con của 4sinh ra bởi các vectơ : u1= (2, -1,3,2) ;
u2= (-1,1,1,-3); u3= (1, 1,9, -5) . Hỏi véctơ u = (3, -1,0, -1) có thuộc không gian con W không? Tại sao?
3.27/ Xét tính độc lập tuyến tính, phụ thuộc tuyến tính của các vectơ sau trong không gian C().
a) 2, 7sin2x, cos2x. b) x, cosx
c) 1, sinx, sin2x. d) 2sin2x, cos2x , cos2x.
e) (1+x)2, x2 +2x, 2. f) 0, x, x2.
g) 1, x, ex, e2x
3.28/ Trong không gian 4cho các véctơ
u1 = (1; 1; 0; 1), u2 = (1; 1; 1; 0) , u3 = (0; 0; -1;1), , u4 = (2; 2; 0;2)
Gọi W là là không gian con của 4bởi các véctơ u1, u2, u3, u4.
a) Xét tính độc lập tuyến tính, phụ thuộc tuyến tính của u1, u2, u3,u4.
b) Tìm số chiều và một cơ sở (gọi tên cơ sở này là B) của không gian con W. Tìm tọa độ vectơ v = (1; 1; 2;-1) đối với cơ sở B.
c) Tìm một cơ sở trực giao của W.
d) Tìm tham số m để véctơ u = (1; m; 1; 2) thuộc không gian con W.
3.29/ Một công ty khai thác mỏ có hai loại mỏ quặng. Hoạt động mỗi ngày tại mỏ I tạo ra lượng quặng có chứa 20 tấn đồng và 550 kilogram bạc, trong khi hoạt động mỗi ngày tại mỏ II tạo ra lượng quặng có chứa 30 tấn đồng và 500 kilogram bạc.
Đặt các vectơ v1=
20
550
và v2=
30. Như vậy v1và v2lần lượt biểu thị “ năng
500
xuất khai thác mỗi ngày “ tại các mỏ I và II tương ứng.
a) Giải thích ý nghĩa của vectơ 5v1?
b) Giả sử công ty khai thác mỏ I trong x1và mỏ II trong x2ngày. Hãy viết một phương trình vectơ mà nghiệm của nó cho biết số ngày mà mỗi mỏ phải khai thác để tạo ra 150 tấn đồng và 2825 kg bạc.
c) Hãy dùng ma trận để giải phương trình trong (b).
3.30/ Một nhà máy điện chạy bằng hơi nước đốt hai loại than: anthracite (A) và bituminuous (B). Ứng với mỗi tấn A được đốt thì nhà máy tạo ra 27,6 triệu Btu nhiệt, 3100 g sulphur đi-ô-xit và 250 g chất thải đặc biệt (particulate matter - các chất ô nhiễm dạng hạt). Ứng với mỗi tấn B được đốt thì nhà máy tạo ra 30,2 triệu Btu nhiệt, 6400 g sulphur đi-ô-xit và 260 g chất thải đặc biệt (particulate matter-các chất ô nhiễm dạng hạt).
a) Lượng nhiệt được tạo ra là bao nhiêu khi nhà máy đốt x1tấn A và x2tấn B?
b) Giả sử công suất nhà máy điện chạy bằng hơi nước được mô tả bằng vectơ liệt kê lượng nhiệt, sulphur đi-ôxit, và chất thải dặc biệt. Hãy biểu diễn vectơ công suất này dưới dạng tổ hợp tuyến tính cúa hai véctơ khi nhà máy đốt x1tấn A và x2tấn B.
c) Giả sử trong một khoảng thời gian liên tục nhà máy tạo ra 162 triệu Btu nhiệt;
2361g sulphur đi-ôxit và 1623 g chất thải đặc biệt. Hãy lập một phương trình véctơ mà nghiệm của nó cho biết có bao nhiêu tấn ứng với mỗi loại than mà nhà máy đã đốt , giải phương trình vectơ này.
3.31/ Đặt v1, v2, ….., vklà các điểm trong R3và giả sử rằng ứng với j = 1,2,……, k một đối tượng có khối lượng mjnằm tại điểm vj. Các nhà vật lý gọi các đối tượng như vậy là các khối lượng điểm. Khối lượng tổng cộng của toàn hệ thống gồm các khối lượng điểm như trên là : m = m1+ m2+……+ mk.
Trọng tâm (tâm khối lượng) của hệ thống là v 1m1v1m2v2 ....... mkvk. Hãy
m
tính tâm khối lượng của hệ thống bao gồm các khối lượng điểm sao đây:
Khối lượng | |
v1=(5, -4, 3) | 2g |
v2=(4, 3, -2) | 5g |
v3=(-4,-3, -1) | 2g |
v4=(-9, 8, 6) | 1g |
Có thể bạn quan tâm!
-
 Toán cao cấp A2 - Trường ĐH Sư phạm Kỹ thuật TP.HCM - 11
Toán cao cấp A2 - Trường ĐH Sư phạm Kỹ thuật TP.HCM - 11 -
 Độ Dài Vectơ (Muđun Vectơ, Chuẩn Vectơ)
Độ Dài Vectơ (Muđun Vectơ, Chuẩn Vectơ) -
 / Trong Các Trường Hợp Sau Đây, Hãy Xác Định Tham Số M Để Véctơ X Là Tổ Hợp Tuyến Tính Của Các Véctơ U, V, W.
/ Trong Các Trường Hợp Sau Đây, Hãy Xác Định Tham Số M Để Véctơ X Là Tổ Hợp Tuyến Tính Của Các Véctơ U, V, W. -
 Biểu Thức Giải Tích Của Tích Hỗn Hợp
Biểu Thức Giải Tích Của Tích Hỗn Hợp -
 Thuật Toán Chéo Hóa Ma Trận Cho A Là Ma Trận Vuông Cấp N.
Thuật Toán Chéo Hóa Ma Trận Cho A Là Ma Trận Vuông Cấp N. -
 Thuật Toán Chéo Hóa Trực Giao Ma Trận Đối Xứng Thực
Thuật Toán Chéo Hóa Trực Giao Ma Trận Đối Xứng Thực
Xem toàn bộ 224 trang tài liệu này.

3.32/ Một vật có khối lượng m được đặt ở cuối lò xo và kéo theo hướng thẳng đứng về phía dưới rồi thả ra, thì hệ vật và lò xo sẽ bắt đầu giao động. Khoảng cách y của vật tính từ vị trí cân bằng được cho bởi hàm
y(t) = c1cos ω t + c2sin ω t (*)
trong đó ω là một hằng số phụ thuộc vào lò xo và khối lượng vật. Chứng minh rằng tập hợp tất cả các hàm được trình bày trong phương trình (*) (với ω coá đònh và c1,c2 tùy ý) là một không gian vectơ. Tìm một cơ sở của không gian này.
3.33/ Cho C() là không gian các hàm số (biến x) liên tục trên với phép cộng
“+” là phép cộng hai hàm số và phép nhân”.” là phép nhân một số thực với một hàm số. Trong C() cho các tập con: A = x, ex, sinx, B = cos3x, cosx, cos3x.
Chứng minh tập A độc lập tuyến tính và B phụ thuộc tuyến tính.
3.34/ Cho không gian 3với tích vô hướng Euclide. Hãy xác định m để các vectơ u,
v trực giao.
a) u = (2, m,3) , v = (1, 3, -4) b) u = (m m,1) , v = ( m, 5, 6) .
3.35/ Trong không gian Euclide nvới tích vô hướng Euclide, hãy viết bất đẳng thức Cauchy – Schwarz và bất đẳng thức tam giác.
3.36/ Trong mỗi trường hợp sau đây, hãy chứng minh là không gian Euclide với
tích vô hướng tương ứng đã chỉ ra.
ÑN b
a) V = C[a,b]; f(x) , g(x) C[a,b]; <f,g> f (x)g(x)dx . Hãy viết bất đẳng thức
a
Cauchy – Schwarz cho tích vô hướng này.
b) V = P2[x] ; f(x) = ao + a1x + a2x2 , g(x) = bo + b1x + b2x2 P2[x]
ÑN
< f, g> ao bo + a1 b1 + a2 b2
c) V = P2[x] ; f(x) = ao + a1x + a2x2 , g(x) = bo + b1x + b2x2 P2[x]
ÑN 1
< f, g> f (x)g(x)dx
0
3.37/ Trong không gian Euclide , chứng minh rằng :
a) u, v
u . v
; u, v ( Bất đẳng thức Cauchy – Schwarz)
b) u v u v ; u, v ( Bất đẳng thức tam giác )
c) Nếu A = u1, u 2,......., u mlà tập trực giao thì
u1 u 2 ... u m
2 u1 2
u 2 2 ... u m
2 ( Định lý Pitago mở rộng )
3.38/ Trong không gian 4với tích vô hướng Euclide, cho tập hợp
B = u1= (1, 1, 1, 2), u2= (1, 2, 3, -3). Chứng minh u1, u2trực giao và bổ sung vào
B hai vectơ nữa để được một cơ sở trực giao của 4.
3.39/ Trong không gian P2[x] xét tích vô hướng
1
< f, g > = f(x).g(x)dx ; với f(x), g(x) P2x.
1
Hãy tính tích vô hướng của f và g trong các trường hợp sau: a) f(x) = 1- x +2x2, g(x) = x – 3x2.
b) F(x) = x + 5x2 , g(x) = 1 + 6x2.
3.40/ Trong không gian 3xét tích vô hướng Euclide. Hãy áp dụng quá trình trực
giao Gram-schmidt để biến cơ sở u1, u2, u3thành cơ sở thực chuẩn. a) u1= (1,1,1), u2= (1,-1,0) , u3= ( 1,2,1).
b) u1 = (1,0,0), u2 = (3,1,-2) , u3 = (0,1,1).
3.41/ Trong không gian P2[x] ( R2[x]) xét tích vô hướng
1
< f, g > = f(x).g(x)dx ; với f(x), g(x) P2x.
1
Hãy áp dụng quá trình trực giao Gram-schmidt để biến cơ sở chính tắc
B = 1, x, x2thành cơ sở trực giao.
3.42/ Trong không gian P2[x] xét tích vô hướng
< f, g > =
f (x). g(x)dx ; với f(x), g(x) P2x.
a) Hãy áp dụng quá trình trực giao Gram-schmidt để biến cơ sở chính tắc
B = 1, x, x2thành cơ sở trực giao.
b) Gọi là không gian con của P2[x] gồm tất cả các phần tử trực giao với u(x) = x2. Tìm một cơ sở trực giao của .
Bài 3.43 và bài 3.44 có dạng là các bái toán phân tích lực trong kỹ thuật và thường gặp nhiều trong điều khiển học.
3.43/ Trong không gian 3với hệ trục tọa độ 0xyz cho các vectơ a = (1;0;1),
b =(2; 1; 1),
c = (-1; 1; 1),
F = ( m +1, m, m+2) với m là tham số. Gọi (P) là mặt
phẳng có cặp vectơ chỉ phương là a , b .
a) Tìm 1, 2, 3 để 1 a + 2 b + 3 c = F .
b) Chứng minh rằng vectơ c vuông góc với mặt phẳng (P) . Tìm vectô u song song
với mặt phẳng (P) và véctơ
v vuông góc với (P) sao cho F = u + v .
3.44/ Trong không gian Euclide 3cho (P) là mặt phẳng có cặp vectơ chỉ phương
là
a = (2,1,1);
b = (1,1,-1) và vectơ lực
F = (1,5,1). Tìm vectô
u song song với mặt
phẳng (P) và véctơ
v vuông góc với (P) sao cho F = u + v . ( Vectô u gọi là vectơ
hình chiếu vuông góc của
F xuống mặt phẳng (P) ký hiệu
hch P F và vectơ
v gọi là vectơ hình
chiếu vuông góc của
F xuống trục vuông góc với (P))
3.45/ Trong 4cho hai không gian con :
W = < u1 = (1,1,-1,0); u2 = (2, 2,1,3)>
U = < v1 = (1,0,1,-1) ; v2 = (2,-1,1,-1)>
Chứng minh W U. Tìm véctơ y W và véctơ z U sao cho x = y + z, với
x (3,1,1,1) .
3.46/ Trong không gian R3cho các véctơ : u1= ( 1, 2, 1); u2= (1, 0, 2) , u3= (3, 2, 5) , v = ( 12, 4, 1) , đặt W = < u1, u2, u3> .
a) Tìm hạng của hệ véctơ u1, u2, u3. Xét tính độc lập tuyến tính, phụ thuộc tuyến tính của hệ véctơ u1, u2, u3.
b) Tìm một cơ sở và số chiều của không gian con W.
c) Tìm véctơ uW và vectơ u’Wsao cho v = u + u’
3.47/ Trong không gian C() các các hàm số thực liên tục trên , cho tích vô
hướng : < f, g > = f (x).g(x)dx ; với f(x), g(x) C()
a) Xác định giá trị hằng số a (nếu có) để tập A=sinx, cosx, axlà tập trực giao.
b) Xác định giá trị hằng số b ( nếu có) để tập A = sinx, 4 + bx +x2là tập trực giao.
3.48/ Trong không gian P2[x] các đa thức bậc bé hơn hoặc bằng 2, cho tích vô
1
hướng: < f, g > = f (x).g(x)dx ; với f(x), g(x) P2x.
0
Tìm các hằng số a, b để tập A = 1, 2x-1, 12ax2+ 6blà tập trực giao.
3.49/ Trong không gian Euclide R3cho (P) là mặt phẳng có cặp vectơ chỉ phương
là
a = (1,2,0);
b = (-1,3,9) và vectơ lực
F = (2,4,7). Tìm vectô
u song song với mặt
phẳng (P) và véctơ
v vuông góc với (P) sao cho F = u + v .
3.50/ Trong không gian 4cho các véctơ
u1 = (1; 1; 0; 1), u2 = (1; 1; 1; 0) , u3 = (0; 0; 1;-1), u4 = (2; 2; 3;-1)
Gọi W là là không gian con của 4bởi các véctơ u1, u2, u3, u4.
a) Xét tính độc lập tuyến tính, phụ thuộc tuyến tính của u1, u2, u3, u4.
b) Tìm tham số m để véctơ u = (3; 3; 1; m) thuộc không gian con W.
c) Tìm một cơ sở trực giao của W.
3.51/ Chứng minh 1, cos x, cos 2x,..., cos(nx)là tập trực giao trong các hàm số liên tục trên [0,] với tích vô hướng
C[0,] -không gian
< f (x) , g(x) > = f (x)g(x)dx
0
với mọi
f (x) ,
g(x) C[0,]
§6. TÍCH CÓ HƯỚNG VÀ TÍCH HỖN HỢP VECTƠ
Phần này chỉ xét các vectơ hình học trong không gian hình học 3 chiều với hệ trục tọa độ Đề-các 0xyz.
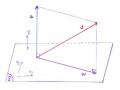
6.1.Tích có hướng vectơ 6.1.1-Định nghĩa
Tích có hướng của hai vectơ và
ký hiệu
hay
hay
, là một vectơ
xác định như sau:
a b a b
a b
a , b
Phương : Vuông góc với mặt phẳng có phương xác định bởi
a , b
Chiều : Được xác định sao cho
a , b , a b
tạo thành tam diện thuận.
Modun :
a b = a . b sin( a , b )
a b
b
S
a
Gọi S là diện tích hình bình hành dựng nên bởi hai vec tơ
a , b
thì
S = a . b sin( a , b ) = a b
6.1.2-Tính chất
a b = Diện tích hình bình hành dựng nên bởi hai vectơ a và b .
a b = 0 a // b .
a b = - ( b a )
(α a ) b = a (α b ) = α( a b ) , α R.
a ( b c ) = a b a c
( a b ) c = a c + b c