Kiến Thức: - Học Sinh Hiểu Định Nghĩa Tứ Giác Nội Tiếp, Tính Chất Về Góc Của Tứ Giác

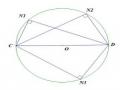
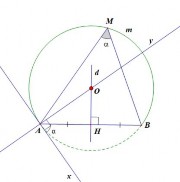
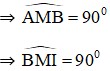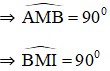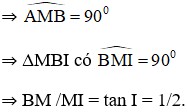cố định tâm O, bán kính

OA.

GV di chuyển điểm M để được tương ứng với góc

nhọn và ứng với góc

tù để học sinh quan sát. (như hình 40a và 40b)

b) Phần đảo:

GV đưa hình 41 trang 85 SGK lên bảng phụ.

Lấy điểm M’ bất kì thuộc cung AmB, ta cần chứng minh AM ' B . Hãy

chứng minh điều đó?

GV chiếu hình 42 (SGK) đã được vẽ sẵn trên phần mềm giúp học sinh quan sát và nhận xét.

Tương tự trên nửa mặt phẳng còn lại cǜng có cung Am’B đối xứng với cung AmB qua AB cǜng có tính chất như trên.

Mỗi cung trên được gọi là một cung chứa góc dựng trên đoạn thẳng AB, tức là cung mà với mọi điểm M thuộc cung

đó, ta đều có AMB .

HS quan sát hình 41 và trả

lời câu hỏi.

HS:

AM ' B BAx (vì đó là góc nội tiếp và góc tạo bởi một tia tiếp tuyến và dây cung cùng chắn cung AnB.)

HS nhận xét.

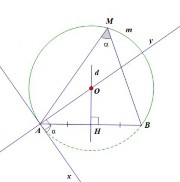
c) Kết luận:

GV đọc kết luận trang 85 SGK và nhấn mạnh để HS ghi nhớ.

GV giới thiệu các chú ý

SGK trang 85, 86.

GV vẽ đường tròn đường kính AB và giới thiệu cung chứa góc 900 dựng trên đoạn thẳng AB.

GV đưa ra chú ý.

2) Cách vẽ cung chứa

góc:

Qua chứng minh phần thuận, hãy cho biết muốn vẽ một cung chứa góc dựng trên đoạn thẳng AB cho trước, ta phải tiến hành như thế nào?

GV vẽ hình trên phần mềm và hướng dẫn HS cách dựng cung chứa góc.

Hai HS đọc kết luận quỹ tích cung chứa góc.

HS vẽ quỹ tích cung chứa góc 900 dựng trên đoạn thẳng AB.

HS lắng nghe, ghi chép.

HS: Ta cần tiến hành:

- Dựng đường trung trực d của đoạn AB.

- Vẽ tia Ax sao cho

BAx .

- Vẽ tia Ay vuông góc với Ax, gọi O là giao điểm của Ay với d.

- Vẽ cung AmB với tâm O, bán kính OA, cung này nằm ở nửa mp bờ AB không chứa tia Ax.

HS vẽ cung chứa góc là

AmB.

Hoạt động 2: Cách giải bài toán quỹ tích (8’)

2. Cách giải bài toán quỹ

- GV: Qua bài toán vừa

HS: Ta cần chứng minh

tích:

nêu trên, muốn chứng

Phần thuận: Mọi điểm có

minh quĩ tích các điểm M

tính chất T đều thuộc hình

a. Phần thuận: Mọi điểm có

thoã mãn tính chất T là

H.

tính chất T đều thuộc hình

một hình H, ta cần tiến

Phần đảo: Mọi điểm thuộc

H.

hành theo những phần

hình H đều có tính chất T.

Phần đảo: Mọi điểm thuộc

nào?

Kết luận: Quỹ tích các

hình H đều có tính chất T.

GV: Xét bài toán quĩ tích

điểm M có tính chất T là

Kết luận: Quỹ tích các điểm

cung chứa góc nói trên

hình H.

M có tính chất T là hình H.

thì các điểm M có tính

chất T là tính chất gì?

Hình H trong bài toán là

gì?

GV lưu ý HS có trường hợp phải giới hạn, loại điểm nếu hình không tồn

tại.

Hoạt động 3: Luyện tập (16’)

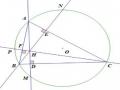
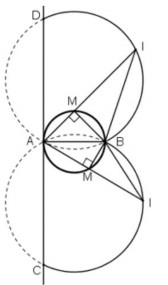
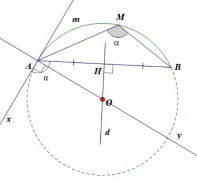
Bài tập 50: (SGK/ 87)

Cho đường tròn đường kính AB cố định. M là một điểm chạy trên đường tròn. Trên tia đối của tia MA lấy điểm I sao cho MI = 2MB.

a) Chứng minh AIB không đổi.

b) Tìm tập hợp các điểm I

nói trên.

Chứng minh

GV yêu cầu HS làm bài

tập 50 (SGK/87).

GV vẽ hình trên phần mềm hình học và hướng dẫn HS vẽ hình theo đề bài.

Yêu cầu HS suy luận tìm

lời giải của bài toán.

a) Chứng minh AIB

không đổi.

GV gợi ý: (nếu cần)

- Góc AMB có số đo

bằng bao nhiêu?

- Có MI = 2MB, hãy xác định góc AIB?

GV yêu cầu HS trình bày ý a vào vở.

HS tìm hiểu đề và vẽ hình theo hướng dẫn của GV.

HS quan sát hình vẽ và vận dụng suy luận tìm cách giải bài toán.

M thuộc đường tròn đường kính AB.

ȍBMI vuông tại M

⇒ tgI = MB 1 .

MI 2

I  2634'

Vậy AIB không đổi.

AB cố định, AIB 2634'

không đổi, vậy I nằm trên

hai cung chứa góc 26034’

dựng trên đoạn thẳng AB.

GV hỏi: Từ kết quả trên

em nhận xét gì về quỹ

tích điểm I.

1 HS lên bảng trình bày lời

giải ý b.

HS dưới lớp làm bài vào

GV yêu cầu HS vẽ 2

vở.

cung chứa góc AIB

dựng trên đoạn AB

GV yêu cầu HS lên bảng

trình bày ý b.

HS nhận xét.

GV yêu cầu HS khác

nhận xét lời giải.

GV nhận xét lời giải của

HS.

Hoạt động của GV

Hoạt động của HS

Hoạt động 1: Tìm hiểu về khái niệm tứ giác nội tiếp (8’)

1. Khái niệm tứ giác nội tiếp:

GV

hiện

yêu

?1

cầu học sinh (sgk/87).

thực

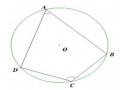
a, Vẽ một đường tròn

HS làm ?1 vào vở.

2 HS lên bảng vẽ hình

HS nhận xét: Tứ giác ABCD có : 4 đỉnh A

, B , C , D  (O)

HS quan sát hình vẽ và đưa ra định nghĩa.

* Định nghĩa ( sgk )

Tứ giác ABDE,

ACDE, ABCD.

tâm O rồi vẽ một tứ giác

có tất cả các đỉnh nằm

trên đường tròn đó.

b, Vẽ một đường tròn

tâm I rồi vẽ một tứ giác

có ba đỉnh nằm trên

đường tròn đó còn đỉnh

thứ tư thì không.

GV yêu cầu 2 HS lên bảng

vẽ hình.

GV chiếu hình vẽ trên phần

mềm hình học.

GV: Yêu cầu HS nhận xét

về 4 đỉnh nằm trong đường

tròn (O) và (I) có đặc điểm

gì khác nhau?

GV: Tứ giác ABCD là tứ

giác nội tiếp. Vậy em

ABCD có A, B, C, D cùng

hiểu thế nào là tứ giác

thuộc đường tròn (O) 

nội tiếp?

ABCD nội tiếp

GV chuẩn hóa lại định

* Định nghĩa: (SGK/87)

nghĩa, yêu cầu HS nhắc

Một tứ giác có bốn đỉnh nằm

lại định nghĩa

trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi là tứ giác nội tiếp).

Bài tập 1: Hãy chỉ ra tứ giác nội tiếp trong hình sau:

GV chiếu bài tập lên bảng. Yêu cầu HS làm việc cá nhân làm bài tập.

Gọi HS đứng tại chỗ trả lời bài tập.