Sử dụng biểu diễn trực quan phát triển năng lực suy luận toán học cho học sinh thông qua dạy học Hình học lớp 9 - 16

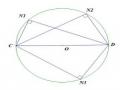
GV yêu cầu HS quan sát trả lời thêm hai câu hỏi sau:

Có tứ giác nào trên hình không nội tiếp đường tròn tâm (O).

Tứ giác AEDM có nội tiếp được đường tròn nào không? Vì sao?

GV cho HS trả lời câu

hỏi đề bài đặt ra.

GV khẳng định lại: Như vậy có những tứ giác nội tiếp được đường tròn có những tứ giác không nội tiếp được đường tròn.

Vậy tứ giác nội tiếp có tính chất gì ta đi tìm

hiểu phần 2.

Tứ giác AKDE

Hoạt động 2: Tìm hiểu về định lí (10’)

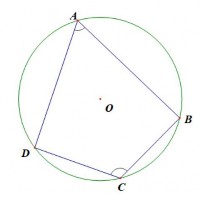
GV chiếu hình 45/SGK

lên bảng yêu cầu HS làm việc theo nhóm làm bài toán: Tính tổng hai góc

A C của tứ giác ABCD. GV yêu cầu đại diện nhóm trình bày cách làm chú ý vào các khâu lập luận của học sinh.

HS làm việc theo

nhóm sử dụng các

2. Định lí:

suy luận để làm bài

Trong một tứ giác nội tiếp,

toán.

tổng số đo hai góc đối

nhau bằng 180.

Đại diện nhóm lên

trình bày.

+) Vì tứ giác ABCD

nội tiếp trong (O ; R )

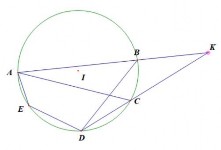
GV nhận xét chuẩn hóa kiến thức yêu cầu HS rút ra định lí.

GV: Theo em nếu một tứ giác có tổng hai góc đối diện có số đo bằng 1800 thì tứ giác đó có nội tiếp được trong một đường tròn không

?

Ta có:

BAD 1 sđ BCD ( 1)

2

(góc nội tiếp chắn cung BCD )

BCD 1 sđ BAD ( 2)

2

(góc nội tiếp chắn cung BAD )

Từ (1) và (2) ta có :

BAD BCD

=

1 (sđ BCD sđ BAD)

2

BAD  BCD 1

2

.3600

BAD  BCD = 1800

* Chứng minh tương

tự ta cǜng có:

ABC  ADC  1800

Vậy trong một tứ giác nội tiếp tổng số đo của 2 góc đối diện bằng 1800

HS dự đoán: Có

GV sử dụng phần mềm hình học vẽ một tứ giác có tổng hai góc đối diện có số đo bằng 1800. Sau đó vẽ đường tròn đi qua 4 đỉnh của tứ giác để HS quan sát.

Từ đây, GV yêu cầu HS rút ra mệnh đề đảo của định lý trên.

HS quan sát.

HS phát biểu.

Hoạt động 3: Định lí đảo (10’)

GV vẽ hình bằng phần mềm hình học. Yêu cầu HS vẽ hình vào vở và suy luận tìm

HS vẽ hình và suy luận tìm cách chứng minh.

cách chứng minh.

GV gợi ý HS chứng

minh:

Vẽ một đường tròn (O)

đi qua ba đỉnh A, B, C

của tứ giác.

3. Định lí đảo:

Vậy để chứng minh tứ

Nếu một tứ giác có tổng số đo hai góc đối nhau bằng 180o thì tứ giác đó nội tiếp được đường tròn.

giác ABCD nội tiếp đường tròn ta cần chứng

minh điều gì?

Hai điểm A và C chia đường tròn thành hai

Ta cần chứng minh D

nằm trên đường tròn

(O).

cung ABC và cung AmC.

Có cung chứa góc B là

Cung AmC chứa góc

cung ABC, vậy cung AmC chứa góc nào?

Tại sao đỉnh D lại thuộc Cung AC .

GV yêu cầu HS về nhà tự chứng minh lại định lý vào vở.

dựng trên 180B đoạn thẳng AC. Theo giả thiết,

B D  180nên

D thuộc (O).

HS về nhà tự chứng minh.

Hoạt động 4: Củng cố - Luyện tập (12’

)

Dạng 1: Chứng minh một tứ giác là tứ giác nội tiếp.

Bài 58 (SGK/90)

GV yêu cầu HS làm bài tập 58/SGK.

HS vẽ hình ghi giả

GV vẽ hình trên phần mềm

thiết kết luận.

và yêu cầu HS vẽ hình vào

HS suy nghĩ làm bài

vở, suy nghĩ

tập.

làm việc độc lập.

GV gọi HS đứng tại

HS nêu cách làm,

chỗ nêu cách làm.

tìm ra con đường

chứng minh.

HS nêu cách chứng

HS còn lại chú ý

minh của mình

nhận xét, so sánh

GV cho HS nêu cách suy

cách suy luận của

luận của mình để tìm ra cách

mình với bạn.

chứng minh cho các bạn

cùng nghe.

GV nhận xét các suy

luận của HS, chuẩn hóa kiến

thức.

Chứng minh

GT

ABC đều

DB = DC, C 1 C

2 2 1

KL

a, ABCD là tứ giác

nội tiếp

b, Tìm tâm đường tròn đi qua 4 điểm A,

B, C, D.

Nếu HS không làm được

GV đưa ra các gợi ý để HS

chứng minh:

Trả lời câu hỏi theo

Để chứng minh tứ giác nội

sự hướng dẫn của

tiếp ta cần chứng minh điều

GV.

gì?

Căn cứ vào giả thiết có thể

vận dụng cách nào trên ba

cách trên?

GV cho HS nêu các ý kiến

của mình, tìm ra cách nào

ngắn gọn dễ hiểu để lựa

HS lên bảng làm bài.

chọn.

Gọi một HS lên bảng

trình bày để rèn khả năng

chuyển từ suy luận ngoại

suy sang suy diễn.

GV chú ý từ (1) và (2) HS

có thể sử dụng định lí đảo

cộng hai góc đối suy ra nội

tiếp luôn nhưng chúng ta

còn đi tìm tâm của đường

tròn nên đưa về dạng quỹ

tích như trên.

GV yêu cầu HS làm bài tập

59/SGK.

HS vẽ hình ghi giả

GV vẽ hình bằng phần mềm

thiết, kết luận.

để HS quan sát và yêu cầu

HS vẽ hình ghi GT, KL vào

HS làm việc theo

vở.

nhóm.

Yêu cầu HS làm việc

theo nhóm, yêu cầu các

nhóm hợp tác làm việc

nghiêm túc, ghi lại ý kiến

của các bạn trong nhóm để

tìm ra cách chứng minh.

Đại diện nhóm lên

Gọi đại diện nhóm lên bảng

bảng trình bày kết

trình bày cách làm của

quả.

nhóm mình nêu cách suy

luận mà nhóm tìm ra

lời giải. GV nhận xét cho

HS trả lời và giải

điểm.

thích tứ giác APBC

GV hỏi thêm tứ giác

là hình thang cân.

APBC là hình gì?

GT

Hình bình hành

ABCD.

Đường tròn đi qua ba điểm A, B, C cắt CD tại P khác C

KL

AP=AD