Sử dụng biểu diễn trực quan phát triển năng lực suy luận toán học cho học sinh thông qua dạy học Hình học lớp 9

II. Phần tự luận: (8 điểm)

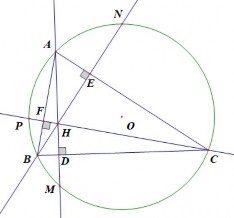
Bài 1: (7 điểm) Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:

a) Tứ giác CEHD nội tiếp

b) Bốn điểm B, C, E, F cùng nằm trên một đường tròn

c) AE.AC = AH.AD ; AD.BC = BE.AC

d) H và M đối xứng nhau qua BC

Bài 2: (1 điểm) Cho góc vuông xOy, điểm A cố định nằm ở trong góc xOy. Một góc vuông quay xung quanh điểm A cắt các tia Ox ở B, cắt tia Oy ở C. Tìm tập hợp các trung điểm M của đoạn thẳng BC.

ĐÁP ÁN

A. Trắc nghiệm: ( 2 điểm)

Học sinh chọn đúng mỗi câu ghi 0.25 điểm.

Câu

1	2	3	4	5	6	7	8
Đáp án	B	D	C	C	A	B	B	C

Có thể bạn quan tâm!

Xem toàn bộ 143 trang tài liệu này.

B.TỰ LUẬN: (8 điểm)

Câu

Nội dung trình bày	Điểm
1.a (1đ)	Hình vẽ đúng a) Xét tứ giác CEHD có: CED  900(do BE là đường cao) HDC  900 (do AD là đường cao) CED HDC  1800 Mà CED và HDC là 2 góc đối của tứ giác CEHD nên CEHD là tứ giác nội tiếp.	0,5đ 0,5đ 0,5đ
1.b (1,5đ)	b) Xét tứ giác BEFC có: BFC  900 (do CF là đường cao) BEC  900 (do BE là đường cao) E và F cùng nhìn BC dưới một góc bằng nhau Tứ giác BFEC nội tiếp được đường tròn Bốn điểm B, E, F, C cùng nằm trên đường tròn	0,5đ 0,5đ 0,5đ
1.c	c, Xét AEH và ADC có:
(2 đ)	AEH ADC  900
	DAC là góc chung
	AEH ~ ADC g.g AE AH
	AD AC AE.AC AD.AH	1đ
	Xét BEC và ADC có
	BEC ADC  900
	ACD là góc chung

BEC ~ ADC g.g 

BEBCAD.BC AC.BE AD AC

1 đ

1.d

d, Tam giác ADB vuông tại D có: A ABC  900 (1)

Tam giác BCF vuông tại F có C ABC  900 (2)

Từ (1) và (2) A1 C1

Mặt khác, ta có A1 C2 (2 góc nội tiếp cùng chắn cung BM)

C1 C2

CD là tia phân giác của góc HCM

Xét tam gác HCM có: CD vừa là tia phân giác vừa là đường cao

HCM cân tại C

CD cǜng là trung tuyến của HM hay H và D đối xứng nhau qua D

(2đ)

0,5đ

(1đ)

a) Phần thuận : OBC có BOC = 90o

OM là đường trung tuyến nên

OM = BC.

ABC có BAC = 90o

AM là đường trung tuyến nên

AM = BC.

Suy ra OM = AM.

OM = AM và O, A cố định, do đó M thuộc đường cố định là đường trung trực của đoạn thẳng OA.

Khi B  O thì M  M1 (M1 là giao điểm của đường trung trực OA với tia Oy).

Khi C  O thì M  M2 (M2 là giao điểm của đường trung trực OA với tia Ox).

Vậy M chuyển động trên đoạn thẳng M1M2 của đường trung trực của đoạn thẳng OA nằm trong góc vuông xOy.

0.25đ

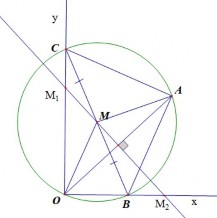
b) Phần đảo : Lấy M bất kì thuộc đoạn thẳng M1M2 ta có

MO = MA. Vẽ đường tròn (M, MO), đường tròn này qua A và cắt

Ox tại B, cắt Oy tại C. BOC = 90o

 BC là đường kính của (M)

 M là trung điểm của đoạn thẳng BC.

c) Kết luận : Tập hợp các trung điểm M của đoạn thẳng BC là đoạn thẳng M1M2 thuộc đường trung trực của đoạn thẳng OA nằm trong góc vuông xOy (M1 và M2 lần lượt là giao điểm của đường trung

trực của đoạn thẳng OA với các tia Oy và Ox).

0.25đ

Phụ lục 5

PHIẾU HỌC TẬP

Họ và tên……………………………………………………………….............…… Lớp:……………………………..........………………………………………………

Phiếu học tập số

Bài toán 1: Cho tam giác ABC về phía ngoài tam giác dựng các tam giác ABD và BCE

vuông cân tại B. Hãy so sánh diện tích tam giác ABC và BDE.

Bài làm

.......................................................................................................................................

Phiếu học tập số 2

Bài toán 2: Cho tam giác ABC vuông tai A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm và 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC.

a, Tính độ dài DE

b, Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M và N.

Chứng minh M là trung điểm của BH, N là trung điểm của CH.

Bài làm

.......................................................................................................................................