Bảng 6.8: Quy về trường hợp hai máy
Thời gian sản xuất (giờ) | ||
Máy A (t1 + t2) | Máy B (t2 + t3) | |
A | 13 + 5 = 18 | 5 + 9 = 14 |
B | 5 + 3 = 8 | 3 + 7 = 10 |
C | 6 + 4 = 10 | 4 + 5 = 9 |
D | 7 + 2 = 9 | 2 + 6 = 8 |
Có thể bạn quan tâm!
-
Mức Dự Trữ Qua Các Tháng Theo Chiến Lược Duy Trì Kế Hoạch Sản Xuất Cố Định Trong 6 Tháng -
Thực Chất Của Điều Độ Sản Xuất Trong Doanh Nghiệp -
Các Chỉ Tiêu Đầu Vào Trong Lịch Trình Sản Xuất Của Doanh Nghiệp X -
Thực Chất Và Yêu Cầu Của Hoạch Định Nhu Cầu Nguyên Vật Liệu (Mrp) -
Những Yêu Cầu Trong Ứng Dụng Hoạch Định Nhu Cầu Nguyên Vật Liệu -
Kết Quả Của Quá Trình Hoạch Định Nhu Cầu Đối Với Cánh Cửa
Xem toàn bộ 215 trang tài liệu này.
0 5 8 18 24 28 31 33
B
A
C
D
B
D
Máy 1
A
C
B
Máy 2
A
C
D
Máy 3
0 15 23 32 37 43
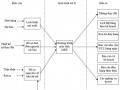
Hình 6.2:Sắp xếp thứ tự công việc theo phương pháp Johnson mở rộng
Vậy thời gian ngắn nhất để thực hiện hết 4 sản phẩm là 43 giờ.
6.2.2. Phân giao công việc cho nhiều máy ở trạng thái động
Trong trường hợp chúng ta phải sắp xếp thứ tự n công việc cho m máy và mỗi công việc đều có đường đi có tới (n! x m) cách sắp xếp. Trong quá trình phân giao công việc lại thường xuyên có các công việc mới được đưa vào, đòi hỏi quyết định phân giao công việc phải bổ sung, cập nhật liên tục để sử dụng thiết bị có hiệu quả hơn. Điều đó có nghĩa là phân giao công việc trong trạng thái động. Việc phân giao khó có thể tìm được phương án tối ưu. Trong trường hợp này có thể áp dụng phương pháp mô phỏng theo nguyên lý “khẩn trương”. Để thực hiện phương pháp này, cần biết số lượng công việc và thời gian thực hiện hoặc số hoạt động phải hoàn thành đối với công việc. Phương pháp này phụ thuộc rất lớn vào hình dạng và cách bố trí các nơi làm việc trong phân xưởng. Có nhiều nguyên tắc ưu tiên phân giao công việc cho từng máy tại từng thời điểm trong trạng thái động, nhưng ưu tiên công việc trong thời gian ngắn nhất là nguyên tắc thực tế đã chứng minh mang lại hiệu quả nhất.
Chúng ta xem xét ví dụ sau: Giả sử có 4 công việc sẽ được đưa vào phân xưởng trong thời gian sắp tới. Các khâu và thời gian thực hiện từng công việc được cho trong bảng sau:
Thời gian đưa vào | Thứ tự và thời gian thực hiện | |
1 | 0 | A (10), B (20), C (35) |
2 | 0 | B (25), A (20), C (30), D (15) |
3 | 20 | B (10), D (10) |
4 | 30 | A (15), C (10), D (20) |
Giả sử công việc 1 phải chế biến đầu tiên ở khâu A, thứ 2 ở khâu B, thứ 3 ở khâu C và thời gian tương ứng là 10, 20, 35 phút và sơ đồ bố trí thiết bị trong phân xưởng theo trình tự:
A B C D
Trường hợp này ta phân giao như sau:
Bắt đầu tại t = 0, sử dụng nguyên lý công việc còn lại ít nhất. Tại thời điểm t = 0, công việc 1 và 2 được đưa đến. Công việc 1 ngay lập tức được sắp xếp lịch vào AL và công việc 2 vào BD. Tình trạng của phân xưởng tại thời điểm t = 0 như sau:
1
2
AL BD CG DM
10 25
Thời điểm t = 0
Trong khoảng thời gian cụ thể chỉ có 2 trường hợp xảy ra: có công việc mới đến hoặc gia công một số công việc xong. Nếu không có gì xảy ra trong khoảng thời gian đó thì chúng ta chuyển sang thời gian sau. Trong ví dụ này không có gì xảy ra trong khoảng thời gian 5 phút, nhưng công việc một hoàn thành ở A sau 10 phút. Vì công việc 2 vẫn còn đang gia công ở B nên tại thời điểm 10 công việc 1 phải chờ. Tình trạng của phân xưởng bây giờ như sau:
1
2
AL BD CG DM 25
Thời điểm t = 10
Không có gì xảy ra vào thời điểm t =15. Tại thời điểm 20, công việc 3 được đưa vào chờ tại B.
1
3
2
A B C D 25
Thời điểm t = 20
Tại thời điểm 25, công việc 2 hoàn thành ở B. Vấn đề đặt ra phải sắp xếp công việc 1 hay 3 vào B. Thời gian còn lại đối với công việc 1 là 20 + 35 = 5 và đối với công việc 3 có tổng thời gian gia công là 10 + 10 = 20. Như vậy, công việc 3 bố trí trước và công việc 2 chuyển sang A.
1
2
3
A B C D
45 25
Thời điểm t = 25
Theo cách này, chúng ta bố trí toàn bộ công việc theo bảng sau:
4
1
2
3
A B C D
45 35
Thời điểm t = 30
4
2
1
A B C D
45 55
Thời điểm t = 35
4
1
2
A B C D
60 55 75
Thời điểm t = 45
1
2
60
75
A
C
B D
Thời điểm t = 55
1
4
2
A B C D 75
Thời điểm t = 60
1
4
A B C D 85
Thời điểm t = 75
4
1
2
A B C D
120 90
Thời điểm t = 85
1
4
A B C D
120 110
Thời điểm t = 90
1
A B C D 120
Thời điểm t = 110
A B C D
Thời điểm t = 120
Trong thực tế, chúng ta còn gặp trường hợp phân giao công việc cho nhiều máy với luồng di chuyển của công việc khác nhau. Có công việc đi qua một số ít máy nhưng cũng có công việc phải đi qua rất nhiều máy. Trong trường hợp này không có giải pháp tối ưu. Để phân giao, người ta sử dụng cách tiếp cận là lý thuyết xếp hàng. Ưu điểm của phương pháp lý thuyết xếp hàng là cho giải pháp tối ưu. Tuy nhiên, việc ứng dụng lý thuyết xếp hàng rất ít khi được sử dụng trong thực tế bởi vì hạn chế của nó là phức tạp và phải đưa ra những giả định về thời điểm công việc đưa vào và thời gian chế biến. Vì vậy, chúng ta không thể xét đến ở đây.
6.2.3. Sử dụng bài toán Hungary trong phân giao n công việc cho n đối tượng
Trong trường hợp sắp xếp hoặc phân giao n công việc cho n máy hoặc n người với điều kiện mỗi máy hoặc mỗi người chỉ đảm nhận một công việc cũng có rất nhiều phương án sắp xếp khác nhau. Trong trường hợp này có thể xác định được phương án sắp xếp tối ưu giữa các phương án đó. Phương án tối ưu có thể là phương án có tổng thời gian thực hiện nhỏ nhất hoặc cung cấp sản phẩm, dịch vụ nhanh nhất, tùy thuộc vào mục tiêu cụ thể đặt ra trong khi sắp xếp. Trong một số trường hợp mục tiêu đặt ra là tổng thời gian thực hiện của tất cả các đối tượng là ngắn nhất nhưng trong các trường hợp khác mục tiêu lại là giảm thời gian ứ đọng khi thực hiện các công việc.
Để xác định được phương án tối ưu ta dùng thuật toán Hungary. Thuật toán này được thực hiện theo trình tự sau :
Bước 1: Lập bảng phân việc và máy theo dữ liệu thực tế;
Bước 2: Tìm số nhỏ nhất trong từng hàng của bảng phân việc và trừ các số trong hàng chosố đó;
Bước 3: Tìm số nhỏ nhất trong từng cột và trừ các số trong từng cột cho số đó;
Bước 4: Tìm cách kẻ các đường thẳng đi qua hàng hoặc cột có các số 0 sao cho số đườngthẳng kẻ được ít nhất. Thực hiện theo cách sau:
- Bắt đầu từ những hàng có 1 số 0, khoanh tròn số đó lại và kẻ một đường thẳng xuyên suốtcột;
- Tìm các cột có 1 số 0, khoanh tròn số đó lại rồi kẻ một đường xuyên suốt hàng.
Bước 5: Lặp lại bước 4 cho đến khi không còn có thể khoanh được nữa. Nếu số đườngthẳng kẻ được ít nhất bằng số hàng (số cột) thì bài toán đã có lời giải tối ưu. Nếu số đường kẻ được nhỏ hơn số hàng (số cột) thì cần làm tiếp: Tìm số chưa bị gạch nhỏ nhất và lấy tất cả các số chưa bị gạch trừ đi số đó; các số bị gạch bởi 2 đường thẳng cộng với số đó; còn các số khác giữ nguyên.
Bước 6: Quay trở lại bước 4 và 5 cho đến khi tìm được lời giải tối ưu.
Ví dụ: Trong một tổ sản xuất có 4 công việc I, II, III, IV cần bố trí cho 4 công nhân A, B, C, D. Chi phí thực hiện cho mỗi công việc của từng công nhân cho ở bảng sau. Tìm phương án bố trí công việc sao cho tổng chi phí thực hiện các công việc là nhỏ nhất.
Đơn vị: phút
I | II | III | IV | |
A | 18 | 52 | 64 | 39 |
B | 75 | 55 | 19 | 48 |
C | 35 | 57 | 8 | 65 |
D | 27 | 25 | 14 | 16 |
Yêu cầu: Tìm phương án bố trí công việc sao cho tổng chi phí thực hiện các công việc là nhỏ nhất.
Dùng thuật toán Hungary ta có cách giải như sau: Bước 1, bước 2:
I | II | III | IV | |
A | 0 | 34 | 12 | 21 |
B | 56 | 36 | 0 | 29 |
C | 27 | 49 | 0 | 57 |
D | 13 | 11 | 0 | 2 |
Bước 3, bước 4:
I
1
0
Công việc Nhân viên
II
III
IV
A
0
23
1
2
19
B
5
6
25
0
27
C
2
7
38
0
55
D
3
0
0
0
4
0
32
0
Công việc Nhân viên
I
II
III
IV
A
1
2
B
56
6
0
8
C
27
19
0
36
D
0
1
9
Bước 5:
0
0
32
0
Công việc Nhân viên
I
II
III
IV
A
4
1
8
B
56
0
0
2
C
21
1
3
0
30
D
0
2
5
Như vậy ta bố trí:
Nhân viên A thực hiện công việc 1 với thời gian là 18 phút; Nhân viên B thực hiện công việc 2 với thời gian là 55 phút; Nhân viên C thực hiện công việc 3 với thời gian là 8 phút; Nhân viên D thực hiện công việc 4 với thời gian là 12 phút;
Tổng thời gian thực hiện công việc của cả 4 nhân viên là 93 phút.
Trong thực tế nhiều khi chúng ta gặp trường hợp phân giao công việc sao cho tổng lợi nhuận thu được tối đa. Để tìm được phương án phân giao tối ưu vẫn sử dụng phương pháp giải trên. Tuy nhiên cần phải đổi dấu toàn bộ các số liệu trong bảng phân việc, sau đó vận dụng thuật toán Hungary giải bình thường.