Sự Cần Thiết Phải Rèn Luyện Và Phát Triển Tư Duy Biện Chứng Cho Học Sinh Trong Dạy Học Môn Toán

dung của hiện thực cần có TDBC và để nhận thức mặt hình thức của hiện thực cần có TD lôgic.

Như vậy, qua phân tích trên ta có thể khẳng định TDBC là tổng hoà cả các loại TD.

1.1.6. Sự cần thiết phải rèn luyện và phát triển tư duy biện chứng cho học sinh trong dạy học môn Toán

a). Nhiệm vụ và mục tiêu đào tạo: Ngày 28/12/2001, Thủ tướng Chính phủ đã ký Quyết định số 201/2001/QĐ - TTg phê duyệt Chiến lược GD 2001 - 2010 như sau: "Nhiệm vụ và mục tiêu cơ bản của GD là nhằm xây dựng những con người và thế hệ ... làm chủ tri thức KH và công nghệ hiện đại, có TD sáng tạo, có kĩ năng thực hành giỏi ... ".

TD sáng tạo là một dạng TD độc lập, tạo ra ý tưởng mới độc đáo và có hiệu quả giải quyết vấn đề cao. TD sáng tạo có ba yếu tố cơ bản: Tính mềm dẻo, tính nhuần nhuyễn và tính độc đáo.

- TDBC góp phần quan trọng và đắc lực trong việc rèn luyện TD sáng tạo cho HS:

Thật vậy: TDBC chỉ rõ: "Khi xem xét sự vật, phải xuất phát từ chính bản thân sự vật" tức là phải xem xét sự vật một cách khách quan, phải hiểu rõ bản chất của sự vật, không được tuỳ tiện, chủ quan, hời hợt dễ dẫn đến sai lầm.

Đây là cơ sở để nhận thức khách thể một cách đúng đắn, để làm chủ tri thức KH và thực hành giỏi. Điều này đòi hỏi HS phải nắm thật vững các thuộc tính bản chất của khái niệm, giả thiết và kết luận của định lí (phạm vi có hiệu lực của định lí), điều kiện đã cho trong BT, ...

VD 1: Khái niệm phép cộng hai vectơ [126, tr. 10].

Định nghĩa: Cho hai vectơ a và b .

Lấy một điểm A nào đó rồi xác định các điểm B và C sao cho AB = a , BC =

b . Khi đó vectơ AC được gọi là tổng của hai vectơ a và b .

Kí hiệu: AC = a + b .

Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.

a

b

a

b

a + b

B

C

A

Hình 1.13: Biểu diễn phép cộng hai vectơ

Khi dạy khái niệm này, GV cần làm cho HS biết:

* Nguồn gốc của khái niệm [137, tr. 100].

Trong thực tế, có những vật cùng một lúc chịu nhiều lực tác dụng lên nó.

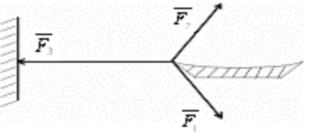
Chẳng hạn: Xét ba lực cùng đặt từ điểm A của một vật rắn có độ lớn bằng nhau và đôi một tạo với nhau cùng một góc bằng 1200.

Chúng được biểu diễn bởi các vectơ AB , AC , AD thuộc một mặt phẳng, lần

lượt bằng

F1 ,

F2 ,

F3 (Hình 1. 14).

Yêu cầu HS giải thích khi đó tại sao vật đứng yên?

Hiện tượng trên giống như khi neo một con thuyền, chịu ảnh hưởng sức đẩy của dòng

nước

F1 , sức gió thổi F2

và sức căng của dây neo

F3 .

Giải thích vì sao thuyền đứng yên, không chuyển động? (Hình 1.14) Yêu cầu HS phân tích, so sánh, giải thích.

Chẳng hạn, trên Hình 1. 14, chiếc thuyền đứng yên vì hợp của hai lực

F1 , F2

là một lực

cân bằng với

F3 . Nghĩa là nếu

F1 F2 F4 , biểu thị bởi vectơ AE thì F3

và F4

ngược

F4

hướng và có độ dài F3 =

. Khi đó, các điểm D, A, E thẳng hàng.

F1

Do góc BAD bằng 1200 và D, A, E thẳng hàng nên góc BAE bằng 600.

F3

Mặt khác, tam giác BAE cân vì AE =

Từ đó tam giác BAE đều.

= = AB.

Lập luận tương tự ta có tam giác EAC là tam giác đều và từ đó suy ra ABEC là

hình bình hành. Vậy,

F2 = AC = BE .

Khi đó người ta nói rằng:

F1 + F2

= AB + BE = AE = F4

(1)

Nhận xét: Nếu thay điểm đặt A của ba lực F1 ,

F2 ,

F3 ; giữ nguyên hướng và độ

lớn. Khi đó ta hình dung: AB = F1 = A' B' (A’ là điểm khác A thuộc vật rắn xét ở trên).

A'C' = F2

= AC ;

A' D' = F3

= AD ;

A' E' = AE là hợp của hai lực trên.

E

B

F4

C

F

1

600

1200

F

A

F3

D

2

Hình 1.14

Hình 1.15

Bằng lập luận tương tự ta cũng có B' E' = BE và từ đó ta có:

F1 + F2

= A' B' +

B' E' =

A' E' = AE = F4

(2)

Từ các hệ thức (1) và (2), chúng ta có nhận xét: Tổng của hai lực F1 + F2 là một lực

F4 không phụ thuộc vào vị trí của điểm đặt, chỉ phụ thuộc vào độ lớn và hướng của chúng.

Tổng quát tình huống trên, cho hai vectơ a , b bất kì trong mặt phẳng, làm thế

nào để xác định tổng a + b . Yêu cầu Học sinh nhận xét dẫn tới:

Đặt từ điểm A vectơ AB = a , tiếp đó đặt từ điểm B vectơ BC = b , khi đó vectơ

AC là tổng của hai vectơ a và b . Viết: AC = a + b .

HS cần nhận xét a + b không phụ thuộc vào việc chọn điểm A.

Hoặc, việc hình thành khái niệm này được mô tả một cách trực quan từ việc tịnh tiến một vật theo những vectơ khác nhau [126, tr. 10].

Từ đó, phép cộng hai vectơ ra đời.

* Bản chất đối tượng

Phép cộng hai vectơ được định nghĩa không phụ thuộc vào việc chọn điểm A ban đầu. Nếu ta chọn một điểm A1 A, thì ta cũng sẽ được:

A1 B1

= a ,

B1C1 = b và

A1C1 = a + b = AC .

GV cần chú ý cho HS: Việc dẫn ra qui tắc 3 điểm được suy trực tiếp nhờ định nghĩa.

+ TDBC chỉ rõ: “Khi xem xét sự vật, phải xem xét một cách đầy đủ với tất cả tính phức tạp của nó”, tức là phải xem xét sự vật trong tất cả các mặt, các mối quan hệ (bên trong và bên ngoài, trực tiếp và gián tiếp) trong tổng thể những mối quan hệ phong phú, phức tạp và muôn vẻ của nó với các sự vật khác. Đây là cơ sở để HS học toán một cách sáng tạo, không gò bó, đưa ra nhiều lời giải khác nhau.

VD 2: Tính khoảng cách từ điểm M(13; 14) đến đường thẳng ( ): 4x 3y + 15 = 0.

4.13  3.14  15

42  32

* Cách 1: áp dụng trực tiếp công thức tính khoảng cách từ một điểm đến một

đường thẳng:

d M ;  5

* Cách 2: Chuyển phương trình ( ) về dạng tham số:

Đường thẳng có vectơ chỉ phương là: u = (3 ; 4) và đi qua N(0 ; 5)

y  5  4t

: x 3t



t R . Gọi H (3t ; 54t).

MH

 3t  1325  4t  142

25t 2 150t  250

25t 2  150t  250

Tính MH = = =

d M ; Min MH

Min

Dùng tính chất của Parabol hoặc xét:

f t  25t 2  150t  250

f ' t  50t

 150

f ' t  0  50t

 150  0 t 3 .

t

		3		+
f 't 			0	+
f t 	+		25	

Có thể bạn quan tâm!

• Các Đặc Trưng Cơ Bản Của Tư Duy Biện Chứng
• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 4
• Mối Quan Hệ Giữa Td Sáng Tạo, Td Độc Lập, Td Tích Cực
• Hoạt Động Hóa Người Học Khi Dạy Học Các Tình Huống Điển Hình
• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 8
• Những Biểu Hiện Của Tdbc Trong Dạy Học Môn Hình Học Ở Trường Thpt

Xem toàn bộ 225 trang tài liệu này.

25

Bảng 1.2: Bảng biến thiên

Do đó

d M ; Min MH 

 5 .

* Cách 3: Chuyển phương trình ( ) về dạng tham số:

Đường thẳng ( ) có vectơ chỉ phương là: u = (3 ; 4) và đi qua N(0 ; 5)

y  5  4t

: x 3t



t R . Gọi

H  3t;5  4t .

Ta có:

MH u MH .u  0

25

 3t  13;9  4t  3;4 0  25t  75  0 t 3

H 9;17

MH

 42 32

d M ; 

 5.

y  14  3t

* Cách 4: Viết phương trình đường thẳng (’) đi qua với (). Suy ra vectơ chỉ phương của (’) là: u' 4;3.

M 13;14

và vuông góc

Phương trình (’):

x  13  4t .



Tọa độ H là nghiệm của hệ:

4x  3y  15  0



x  13  4t



y  14  3t

1

2

3

Thay (2) và (3) vào (1), ta có:

 25t  25  0

t 1

413  4t  314  3t  15  0

Thay vào (2) và (3), ta được:

x  9



y  17

H 9;17.

MH

d M ; 

 42 32

 25  5.

b). Bất cứ sự vật nào cũng là một thể thống nhất của các mặt đối lập và luôn luôn có sự mâu thuẫn giữa các mặt đối lập. Sự mâu thuẫn ấy chính là nguồn gốc động lực bên trong của sự phát triển đối với các sự vật và hiện tượng.

Mặt đối lập là sự khái quát những mặt, những thuộc tính, những khuynh hướng trái ngược nhau trong một chỉnh thể làm nên sự vật và hiện tượng. Thống nhất là hai mặt đối lập liên hệ với nhau, ràng buộc nhau và quy định lẫn nhau, mặt này lấy mặt kia làm tiền đề tồn tại cho mình. Mâu thuẫn giữa các mặt đối lập nghĩa là các mặt đối lập phủ định nhau.

Như vậy, khi xem xét sự vật, chủ thể cần nhận thức rằng bao giờ cũng vậy bất cứ sự vật hoặc hiện tượng nào cũng là một thể thống nhất bao gồm những mặt, những thuộc tính, những khuynh hướng trái ngược nhau, mâu thuẫn với nhau, làm cho sự vật phát triển.

Chẳng hạn: Sự phát triển của hệ thống số.

c). TDBC chỉ rõ: "Phải xem xét sự vật trong sự mâu thuẫn và thống nhất" giúp HS học toán một cách chủ động và sáng tạo, thể hiện ở khả năng phát hiện vấn đề và định hướng cho cách giải quyết vấn đề.

Phát hiện vấn đề: Với TDBC, ta sẽ thấy rằng câu trên là đúng mà chưa thật đúng. Tại sao? Nó là đúng, nếu ta đứng ở góc độ nhìn hình thoi (cái riêng) và hình bình hành (cái chung) là "mâu thuẫn" với nhau. Nó không thật đúng, nếu ta nhìn hai hình đó là "thống nhất" với nhau: Hình thoi là một trường hợp đặc biệt của hình bình hành. Khi đó, ta sẽ không nghĩ rằng hình bình hành không có tính chất đó mà phải nghĩ rằng hình bình hành ắt có tính chất tổng quát hơn, nhận tính chất A làm một trường hợp đặc biệt. Và thế là, có cái gì đó thôi thúc ta tự hỏi: " Vậy tính chất tổng quát hơn đó là cái gì?".

Giải quyết vấn đề: Nếu ta nhìn các đường chéo của hình thoi như là các đường phân giác của các góc thì một nghi vấn KH sẽ nảy sinh: "Vậy trong một hình bình hành không phải là hình thoi thì bốn đường phân giác sẽ như thế nào?", trả lời câu hỏi này, dễ thấy ra tính chất sau đây:

Tính chất B: Trong một hình bình hành, bốn đường phân giác tạo nên một hình chữ nhật.

A a

1

2

N

b

M

P

2

1

Q

C

Chứng minh tính chất B:

Ta có:

AˆBˆCˆDˆ  3600

(1) B

Mà AˆCˆ

(2)

BˆDˆ

(3)

Thế (2) và (3) vào (1), ta được:

AˆBˆCˆDˆ  3600

 2 Aˆ 2Dˆ 3600

AˆDˆ 1800

D

Hình 1.16: Hình vẽ chứng minh tính chất B

hay

2 Aˆ

 2Dˆ1

 1800

1

0

Aˆ1Dˆ1 90

Mˆ  900. Tương tự: QˆNˆ

Pˆ  900 .

Do đó MNPQ là hình chữ nhật.

Ngoài ra, nếu

a, ba b

là hai cạnh của hình bình hành và là góc không tù

của nó 0  900 thì các cạnh của hình chữ nhật này sẽ là:

MQ AQ AM

a.sin b.sin a b.sin .

2 2 2

MN DN DM

a.cos b.cos a b.cos .

2 2 2

Như thế, tính chất A là một trường hợp đặc biệt của tính chất B khi a = b.

1.1.7. Tư duy biện chứng có thể rèn luyện và phát triển cho học sinh khi dạy học môn Toán

- Nói về vai trò của Toán học trong nhận thức KH, F. Ăngghen đã viết: "Muốn nhận thức BC và đồng thời duy vật về tự nhiên, cần hiểu biết Toán học và KH tự nhiên" và F. Ăngghen cũng cho rằng Toán học là những hình dạng KG và quan hệ số lượng của thực tại. Ở đây, cái đặc biệt quan trọng là chỗ Toán học được xem như một KH nghiên cứu những mặt xác định của thế giới hiện thực, có một nguồn gốc vật chất hoàn toàn thực tế" [130, tr. 50].

Theo trên, Toán học không phải chỉ là một lĩnh vực nhất định của tri thức mà còn là một PP và một dạng nhất định của nhận thức KH, nó góp phần xây dựng chính các lí thuyết KH.

Chính Viện sĩ Côlmôgôrôv A. N. khẳng định: "Về nguyên tắc thì phạm vi ứng dụng PP Toán học không hạn chế: Tất cả các dạng vận động đều có thể nghiên cứu theo kiểu Toán học" [130, tr. 195].

Qua DH toán cho HS phổ thông, có thể góp phần rèn luyện và phát triển TDBC.

VD 1: Khái niệm cộng hai vectơ (VD đã xét).

Khái niệm cộng hai vectơ ra đời và xuất phát từ nhu cầu thực tế của cuộc sống, xuất phát từ BT thực tế tìm hợp các lực cùng tác dụng vào một vật, tức là xuất phát từ thực tế “khách quan”, đó là thể hiện quy luật “khách quan” của TDBC.

Từ một việc cụ thể trong “thực tế”, Toán học đã khái quát và “trừu tượng hóa” từ đó đưa ra một định nghĩa thuần túy Toán học: Khái niệm cộng hai vectơ.

Từ định nghĩa này, khái niệm cộng hai vectơ lại được áp dụng một cách rất phổ biến và hiệu quả trong thực tiễn như: tìm hợp của các lực cùng tác dụng vào một vật vào cùng một thời điểm.

Điều này thêm một lần nữa thể hiện vai trò của TDBC qua quy luật: “Từ trực quan sinh động đến TD trừu tượng, từ TD trừu tượng đến thực tiễn”. Mặt khác, nó cũng giúp HS cảm nhận được quy luật và nhằm hình thành trong họ quy luật đó, để phát triển hơn năng lực TDBC.

VD 2: Khái niệm đạo hàm (Giải tích)

BT tìm vận tốc tức thời của một chất điểm chuyển động thẳng.

Cho một chất điểm M chuyển động trên trục s’0s. Hoành độ OM = s của chất

điểm là một hàm số của thời gian t.

s’ .

thời điểm t0 s

.

OM = s = f(t) O M

(Hệ thức s = f(t) được gọi là phương trình chuyển động). Hãy tìm vận tốc của chất điểm tại thời điểm t0.

Để đơn giản ta giả sử s = f(t) là một hàm số tăng của t.

Bây giờ, ta hãy khảo sát chuyển động trong thời gian t từ thời điểm t0 đến thời điểm t0+ t. Ở thời điểm t0 chất điểm M có hoành độ s0 = f(t0).