Kiến Thức Thống Kê Để Dạy Học (Skt) Theo Gonzalez (2014)

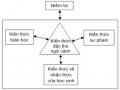
nội dung sư phạm bao gồm kiến thức về việc học của HS (Knowledge of Content and Student, KCS), kiến thức về việc dạy (Knowledge of Content and Teaching, KCT) và kiến thức chương trình (Knowledge of Content and Curriculum, KCC).

2.1.1. Kiến thức nội dung phổ biến

Theo Ball, Thames và Phelps (2008), CCK là những kiến thức về nội dung toán học và kĩ năng mang tính phổ biến, thông thường, được sử dụng trong nhiều môi trường khác nhau trong cuộc sống, không chỉ dành riêng cho giảng dạy, mà một người học toán ở cấp phổ thông có thể biết được.

Với một chủ đề kiến thức đưa ra, theo Ball, Thames và Phelps (2008), những mô tả sau liên quan đến CCK của GV:

• Trả lời đúng hay giải thích chính xác các vấn đề toán học thông thường;

• Nhận ra khi HS của họ trả lời sai hoặc khi một khái niệm nào đó được trình bày không chính xác;

• Sử dụng những khái niệm, thuật ngữ, kí hiệu, hay quy trình thuật toán thông thường vào giải quyết những vấn đề thực tế trong cuộc sống hàng ngày.

Ví dụ về CCK bao gồm kiến thức về các phép toán cộng, trừ các số tự nhiên thông thường, cách tính chu vi hay diện tích của một mảnh đất bằng cách vận dụng công thức tính của hình vuông, hình chữ nhật hay cách đếm và sắp xếp các đối tượng điều tra vào các nhóm khác nhau trong thống kê…Tuy nhiên việc giải thích, phân tích sâu sắc hay kết nối sự biểu diễn khác nhau của những kiến thức đó trong các ngữ cảnh cụ thể lại thuộc phạm vi của kiểu kiến thức khác (đó là SCK).

2.1.2. Kiến thức nội dung đặc thù

SCK được định nghĩa là “kiến thức và kĩ năng toán học chỉ có ở GV cần để thực hiện công việc của họ” (Ball, Thames, & Phelps, 2008, trang 400). Đây không đơn thuần chỉ là kiến thức toán về một nội dung nào đó, mà còn là hiểu biết liên quan đến kiến thức đó trong ngữ cảnh dạy học, chẳng hạn như bình luận về một lời giải bài toán của HS, hay xác nhận tính đúng, sai của lời giải đó. Khi nghiên cứu kiến thức này, các nhà nghiên cứu xác định rằng loại kiến thức này là kiến thức toán học cần thiết cho riêng mục đích giảng dạy. Theo Ball và cộng sự (2008), kiến thức nội dung đặc thù của GV có thể được thể hiện qua những gợi ý sau:

• Trình bày, giải thích và đưa ra ví dụ minh họa cho các ý tưởng toán học;

• Giải thích, đánh giá tính hợp lí, tính đúng sai cho các câu trả lời của HS trong ngữ cảnh dạy học;

• Sử dụng một biểu diễn hay liên kết các biểu diễn khác nhau của một khái niệm, đối tượng toán học;

• Thẩm định và điều chỉnh nội dung toán học của sách giáo khoa;

• Thiết kế, sửa đổi các nhiệm vụ toán học sao cho trở nên dễ dàng hơn hoặc khó hơn đối với HS;

• Lựa chọn và phát triển các định nghĩa toán học, các mục đích cụ thể mang tính khả dụng với HS trong dạy học.

Có thể bạn quan tâm!

Xem toàn bộ 277 trang tài liệu này.

Tổng hợp lại, những nhiệm vụ này đòi hỏi sự hiểu biết và suy luận toán học chuyên biệt của GV. Việc giảng dạy đòi hỏi GV phải có những kiến thức vượt ra ngoài kiến thức được dạy cho HS. Chẳng hạn, hiểu được hằng

đẳng thức ab2a2 2ab b2

là một kiểu kiến thức nội dung

chung. Nhưng để việc dạy hằng đẳng thức đó được hiệu quả, người GV cần thiết phải biết minh hoạ hình học khai triển trên

dưới dạng diện tích của hình vuông kích thước a b

thì bằng tổng diện tích của hai

hình vuông có kích thước lần lượt là a và b và tổng diện tích hai hình chữ nhật bằng nhau có kích thước hai cạnh là a và b . Rõ ràng, hiểu biết về minh hoạ hình học của hằng đẳng thức này là một kiểu kiến thức đặc thù cho việc dạy học, gọi là SCK (Thương, 2019).

2.1.3. Kiến thức theo chiều ngang

Kiến thức theo chiều ngang (HCK), theo Ball, Thames và Phelps (2008, trang 403), định nghĩa là "nhận thức về cách các chủ đề toán học có liên quan trong phạm vi toán học được đưa vào chương trình giảng dạy". Cụ thể, HCK là việc hiểu biết về các chủ đề toán trong chương trình có mối liên hệ với nhau như thế nào, về sự kết nối của các mạch kiến thức, đó cũng là sự hiểu biết về các ngữ cảnh toán học rộng hơn trong đó chứa đựng các chủ đề toán học được giảng dạy trong chương trình. Ball, Thames và Phelps (2008) nói rằng họ chưa chắc chắn lắm về sự phân loại HCK. Theo Jakobsen và cộng sự (2012), bản chất của HCK trong mối quan hệ với dạy học là không rõ ràng. Trong một nghiên cứu gần đây Zazkis và Mamolo (2011) đã mô tả HCK theo chiều hướng là xem toán sơ cấp theo quan điểm toán cao cấp và họ lập luận rằng toán học cao cấp là một khía cạnh quan trọng của việc giảng dạy

kiến thức. Tuy nhiên, các nhà nghiên cứu cho rằng HCK có thể hỗ trợ GV trong việc định hướng giảng dạy cho môn học, trong việc đưa ra đánh giá về điều gì là quan trọng về mặt toán học trong một tình huống giảng dạy (Mosvold & Fauskanger, 2014). Từ quan điểm của các nhà nghiên cứu, chúng tôi cho rằng HCK được mô tả bởi những đặc trưng sau:

• Hiểu được nội dung toán học có mối liên quan như thế nào đến chương trình các cấp lớp;

• Thể hiện được các kết nối giữa các chủ đề và các mạch kiến thức trong chương trình;

• Liên kết được kiến thức toán sơ cấp và kiến thức toán cao cấp để có thể nhìn nhận một cách tổng quát hơn.

2.1.4. Kiến thức về việc học của học sinh

KCS đó là kiến thức kết hợp của GV về việc HS hiểu nội dung toán như thế nào với chính nội dung toán học đó. GV phải đoán trước những gì HS có thể nghĩ và những gì họ sẽ cảm thấy khó hiểu. Những GV có kiến thức này tốt thì thường có khả năng xem xét được cách thức HS học một khái niệm hay nội dung toán học như thế nào, hoặc quan tâm đến những lỗi sai hay quan niệm sai thường gặp của HS về nội dung toán học đó. Điều này dẫn đến một sự hiểu biết sâu sắc về tư duy của HS và những gì khiến việc học toán của HS là dễ hay khó (Ball et al., 2008). Theo Ball và cộng sự (2008), các biểu hiện sau nhằm mô tả kiến thức về việc học của HS:

• Hiểu và dự đoán những khó khăn sai lầm của HS;

• Hiểu biết sâu sắc về cách thức HS tư duy và giải thích những suy nghĩ chưa hoàn thiện của HS;

• Dự đoán những gì sẽ tạo hứng thú cho HS khi học một vấn đề cụ thể.

Trọng tâm của những nhiệm vụ này là kiến thức về quan niệm chung của HS và quan niệm sai lầm về nội dung toán học cụ thể. Ví dụ khi dạy về các số đặc trưng đo xu thế trung tâm, GV biết rằng HS sẽ dễ mắc sai lầm như hiểu nhầm giá trị trung vị là giá trị trung bình hay xác định trung vị là giá trị ở giữa của dãy dữ liệu mà không xét đến tần số tương ứng của chúng.

Ball, Thames và Phelps (2008) giải thích cách thức hoạt động của ba loại kiến thức CCK, SCK và KCS trong lớp học nhằm hiểu rõ hơn bản chất của mỗi loại kiến thức như sau:

“Nhận biết một câu trả lời sai là CCK, trong khi xác định bản chất của lỗi, đặc biệt là một lỗi không quen thuộc, thường đòi hỏi sự nhanh nhẹn trong suy nghĩ về các con số, chú ý đến các mẫu và tư duy linh hoạt về ý nghĩa theo những cách đặc biệt của chuyên ngành là SCK. Ngược lại, việc làm quen với các lỗi phổ biến và quyết định lỗi nào trong số các lỗi mà HS dễ mắc phải nhất là những ví dụ về KCS.” (tr. 401)

2.1.5. Kiến thức về việc dạy

KCT là sự kết hợp giữa hiểu biết về giảng dạy và hiểu biết về toán học, cụ thể đề cập đến kiến thức về việc làm thế nào để thiết kế một hoạt động dạy học nhằm phát triển việc hiểu toán ở HS và về việc định hình dạy một nội dung toán học như thế nào. Để dạy học hiệu quả một nội dung toán học nào đó, ngoài hiểu biết về kiến thức toán học liên quan đến nội dung đó, GV cần am hiểu cách thức thiết kế và tổ chức việc dạy học nội dung đó, cũng như kết hợp hai kiểu kiến thức này. GV đôi lúc cần phải biết chọn ví dụ nào để tiếp cận nội dung bài học, ví dụ nào để giúp HS hiểu sâu hơn nội dung toán học đang đề cập. Trong quá trình dạy học trên lớp, GV cũng cần phải biết khi nào thì cần đặt câu hỏi để làm sáng tỏ vấn đề hơn, khi nào thì đặt ra một câu hỏi hay nhiệm vụ mới để thúc đẩy HS đào sâu suy nghĩ hơn. GV phải biết đánh giá những ưu điểm và nhược điểm của các cách thức được sử dụng để dạy một ý tưởng cụ thể và xác định những phương pháp và quy trình khác nhau phù hợp cho việc giảng dạy. Mỗi một vấn đề trên đều đòi hỏi một sự tương tác và kết hợp giữa hiểu biết về kiến thức toán của một nội dung cụ thể và hiểu biết về các vấn đề sư phạm và dạy học ảnh hưởng đến việc học tập của HS. Theo Ball, Thames và Phelps (2008) phân tích, chúng tôi rút ra những khía cạnh sau được xem là thuộc kiểu kiến thức về việc dạy KCT:

• Khả năng lên kế hoạch, thiết kế bài giảng, sắp xếp các nhiệm vụ và hoạt động phù hợp với nội dung toán học;

• Khả năng tổ chức dạy học, lựa chọn những phương pháp, kĩ thuật dạy học phù hợp với nội dung toán học;

• Khả năng đưa ra những tình huống sư phạm và xử lí một cách hiệu quả;

• Am hiểu đối tượng HS, kiến thức của HS để từ đó có chiến lược dạy học phù hợp nâng cao kiến thức cho họ.

Một ví dụ về KCT là khi dạy về biểu đồ histogram, GV cần phải biết lựa chọn bài tập phù hợp để làm rõ bản chất của biểu đồ histogram là tần số, tần suất được tính theo đơn vị diện tích của các cột, đồng thời giúp HS phân biệt được rõ biểu đồ cột và biểu đồ histogram vì về mặt hình thức hai biểu đồ này tương tự nhau. Bên cạnh đó, GV phải thiết kế được các câu hỏi dẫn dắt trong quá trình dạy học giúp HS chủ động lĩnh hội kiến thức.

2.1.6. Kiến thức về chương trình

KCC là kiến thức về việc các chủ đề, quy trình, khái niệm cụ thể được đưa vào trong chương trình ở mỗi cấp, lớp như thế nào, cùng với mối quan hệ giữa chúng. Bên cạnh đó, GV không chỉ biết về nội dung, mục tiêu, yêu cầu HS cần đạt của chương trình, mà còn phải biết sử dụng nội dung chương trình như thế nào thiết kế, thực hiện bài học nhằm thúc đẩy việc hiểu toán và hướng đến phát triển các năng lực cốt lõi của HS. Về cơ bản, khái niệm kiến thức về chương trình của Ball, Thames và Phelps (2008) tương ứng với kiến thức chương trình của Shulman (1986) và có thể được mô tả bởi những khía cạnh sau:

• Hiểu rõ cấu trúc của chương trình giảng dạy và hiểu được vị trí, vai trò của một nội dung toán cụ thể trong chương trình;

• Nắm rõ được mục tiêu, yêu cầu cần đạt của chương trình cũng như mục đích của nội dung toán cụ thể được đưa vào chương trình;

• Biết vận dụng sự hiểu biết về chương trình để thiết kế dạy học nhằm phát triển các năng lực cần thiết cho HS.

Mô hình kiến thức toán để dạy học của Ball và cộng sự (2008) đã và đang được nhiều nhà nghiên cứu và thực hành dạy học toán quan tâm. Điều này chứng tỏ tầm quan trọng và ý nghĩa của việc nắm vững các kiểu kiến thức cần thiết cho việc dạy hiệu quả một chủ đề toán học nào đó ở phổ thông. Hiển nhiên, đóng góp lớn nhất của mô hình phân loại của Ball và cộng sự là chỉ rõ sự tồn tại và phân biệt giữa sáu kiểu kiến thức trên. Trong đó, theo nhiều nhà nghiên cứu, sự nhấn mạnh đến SCK là đóng góp quan trọng của nhóm nghiên cứu của Ball và cộng sự (2008). Tuy vậy, theo các nhà nghiên cứu, vẫn có những hạn chế trong mô hình phân loại của Ball và cộng sự (2008). Chẳng hạn, có những lúc sự phân biệt giữa các CCK và SCK chưa thật sự rõ. Mô hình của Shulman (1986) hay Ball và cộng sự (Ball, Thames, và Phelps, 2008) là một mô hình phát triển năng lực nghề nghiệp của GV

toán định hướng nhận thức (Kaiser et al., 2016). Trong khi đó, các thực hành dạy học của GV thường còn chịu ảnh hưởng của các yếu tố như niềm tin, quan niệm về toán học của GV, tình huống và ngữ cảnh dạy học. Vì vậy, một số nhà nghiên cứu cho rằng cần kết hợp xem xét sự thể hiện của các kiểu kiến thức của GV trong tình huống và ngữ cảnh dạy học cụ thể trong lớp học.

2.2. Kiến thức thống kê để dạy học

Giảng dạy thống kê ở trường phổ thông đã và đang được chú trọng và nhấn mạnh trong nhiều cải cách chương trình giảng dạy toán học được tiến hành gần đây ở nhiều nước trên thế giới. Do đó, ngày nay các GV dạy toán trung học phải dạy một số ý tưởng liên quan đến độ phân tán của dữ liệu, các cách biểu diễn trên đồ thị và cách lấy mẫu là công việc đòi hỏi họ những năng lực đặc trưng chuyên biệt mà nếu như không có mục tiêu của chương trình giảng dạy toán liên quan đến thống kê không thể đạt được. Trong giáo dục thống kê, rất ít nghiên cứu có thể được tìm thấy trong các tài liệu tập trung vào cả hai vấn đề: kiến thức nội dung môn học (SMK) và kiến thức sư phạm (PCK) bằng cách giảng dạy các nội dung liên quan đến độ phân tán giúp học sinh đạt được các mục tiêu giáo dục thống kê (Groth, 2007; Burgess, 2011) cũng như về niềm tin vào việc giảng dạy và học tập các nội dung thống kê (Pierce & Chick, 2011) và các quan niệm thống kê về độ phân tán (González, 2014) được tổ chức bởi các GV. Do đó, không có gì đáng ngạc nhiên khi các nhà nghiên cứu kêu gọi cho việc nghiên cứu về các lĩnh vực thống kê, đặc biệt cho các nghiên cứu về kiến thức chuyên môn và thực hành trong việc dạy độ phân tán, cũng như niềm tin của giáo viên về thống kê và về những khía cạnh của thống kê nên được giảng dạy trong các trường học và các quan niệm về độ phân tán được tổ chức ở trường bởi các GV như thế nào (Gonzalez, 2014).

Dựa trên mô hình MKT của Ball và cộng sự, Gonzalez (2014) giới thiệu một khung lí luận về năng lực chuyên môn của GV toán để giảng dạy các nội dung liên quan đến độ phân tán (variability) trong thống kê. Mô hình này có hai mặt: một mặt là nhận thức và một mặt là phi nhận thức. Mặt nhận thức là một khái niệm hoá sáu phần của SKT, bao gồm tất cả sáu cấu trúc nhận thức được xác định bởi Ball và cộng sự (2008) trong mô hình MKT của họ. Với mô hình này CCK sẽ được nhìn nhận như là sự hiểu biết về thống kê, nghĩa là kiến thức và kĩ năng toán học mong đợi từ bất kì người trưởng thành được giáo dục tốt nào cũng có để đáp ứng các trường hợp thống

kê. Khía cạnh phi nhận thức của mô hình đề xuất ở đây bao gồm hai thành phần là niềm tin của GV về việc dạy và học thống kê và quan niệm của GV về mô hình MKT. Niềm tin ở đây được định nghĩa bởi Philipp (2007) là "những hiểu biết về mặt tâm lí, cơ sở hoặc các mệnh đề về thế giới được cho là đúng", bên cạnh đó nhiều nhà nghiên cứu (Philipp, 2007; Batanero & Díaz, 2010) coi niềm tin là những đặc điểm dường như ảnh hưởng đến mọi khía cạnh của việc giảng dạy toán học, cũng như để xác định kiến thức và niềm tin liên quan đến toán học mà HS có thể đạt được.

Hình 2.2. Kiến thức thống kê để dạy học (SKT) theo Gonzalez (2014)

Để cung cấp một khung đánh giá đầy đủ cho SKT, Gonzalez (2014) đã xây dựng bộ chỉ số để đánh giá 6 kiểu kiến thức của SKT. Mỗi kiểu kiến thức được đánh giá bởi hai chỉ số định tính được xây dựng dựa trên định nghĩa của từng kiểu kiến thức được xác định bởi nghiên cứu. Dựa vào mô hình đó, tác giả đã thiết kế các nhiệm vụ toán để đánh giá các kiểu kiến thức khác nhau của GV để dạy học thống kê.

Nghiên cứu của Gonzalez (2014) đã bước đầu đề cập một cách tổng thể đến cả sáu thành phần của SKT theo mô hình MKT và vai trò của niềm tin, quan niệm của GV về độ phân tán của dữ liệu. Tuy nhiên, nghiên cứu này chỉ được thực hiện trên bốn GV toán học nam ở một trường trung học của Nhật Bản, phạm vi nghiên cứu

còn hạn hẹp, đối tượng tham gia vào nghiên cứu còn ít. Vì vậy cần có nhiều nghiên cứu tiếp theo để nghiên cứu khả năng chuyên môn của GV toán học để giảng dạy thống kê ở trường trung học.

2.3. Nghiên cứu bài học

NCBH là một phương pháp tiếp cận phát triển nghề nghiệp GV dựa trên sự hợp tác có nguồn gốc từ Nhật Bản, Trung Quốc (Fernandez & Yoshida, 2004; Lewis & Tsuchida, 1998; Stigler & Hiebert, 1999; Chen & Yang, 2013) và đã lan rộng trên toàn cầu. Lần đầu tiên được giới thiệu ở Hoa Kì vào cuối những năm 1990, NCBH đã nhanh chóng thu hút sự chú ý của các nhà giáo dục Hoa Kì. NCBH lúc đó được coi là một đổi mới có hiệu quả và có thể áp dụng trong dạy học (Choksi & Fernandez, 2004; Lewis et al., 2004; National Research Council, 2002; Richardson, 2004; Takahashi & Yoshida, 2004). Mặc dù được nhiều nhà nghiên cứu giáo dục quan tâm để phát triển chuyên môn cho GV, NCBH vẫn còn tương đối mới đối với các quốc gia bên ngoài Nhật Bản. Hầu hết các trường học và GV đang ở giai đoạn đầu áp dụng và thực hiện đổi mới thực hành dạy học thông qua NCBH (Murata, A., 2011).

NCBH được xây dựng dựa trên sự phát triển tập thể của phương pháp giảng dạy hiệu quả thông qua làm việc hợp tác và phản ánh về thực hành. Do đó, NCBH cung cấp rất nhiều cơ hội để nâng cao việc giảng dạy toán học (Corcoran & Pepperell, 2011). NCBH đề cập đến một quá trình GV cố gắng cải thiện phương pháp giảng dạy của mình bằng cách làm việc hợp tác với các GV khác để kiểm tra và phản ánh về các thực hành dạy học. Mục đích của NCBH là đạt được những ý tưởng mới về việc dạy và học dựa trên sự hiểu biết tốt hơn về việc học của HS, vì vậy việc quan sát các bài học nghiên cứu thực tế là cốt lõi của quá trình NCBH. Tuy nhiên, NCBH yêu cầu nhiều yếu tố hơn so với nghiên cứu các câu trả lời của HS trong khi quan sát một bài học. NCBH đòi hỏi nhiều thời gian cho một quá trình GV hợp tác để nghiên cứu tất cả các khía cạnh chuyên sâu nội dung bài học nghiên cứu sẽ được giảng dạy, tài liệu giảng dạy, đánh giá sau bài học và thậm chí có sự tham gia của các chuyên gia, chẳng hạn như giảng viên đại học, đóng vai trò làm người cố vấn hay điều khiển (Takahashi, Watanabe, Yoshida & Wang- Iverson, 2005). Tính năng chính của NCBH là lập kế hoạch hợp tác, góp ý, thảo