Những Nhầm Lẫn Thường Gặp Giữa Biểu Đồ Cột Và Biểu Đồ Histogram

CHƯƠNG 3

KIẾN THỨC CỦA GIÁO VIÊN ĐỂ DẠY HỌC THỐNG KÊ

Ở chương này, chúng tôi trình bày một số kiến thức cơ sở về biểu đồ cột và biểu đồ histogram, các số đặc trưng đo xu thế trung tâm. Bên cạnh đó, chúng tôi xây dựng bộ chỉ số về kiến thức của GV để dạy học biểu đồ cột và biểu đồ histogram, các số đặc trưng đo xu thế trung tâm và độ phân tán của dữ liệu trên biểu đồ cột và biểu đồ histogram nhằm làm cơ sở để tiến hành các bước trong thực nghiệm được trình bày ở chương sau.

3.1. Sơ lược tri thức luận và lịch sử thống kê

Nhiều nghiên cứu về lịch sử của thống kê cho cho thấy rằng Thống kê học ra đời và phát triển theo yêu cầu của xã hội. Để làm rõ cho nhận định này người ta thường điểm lại lịch sử thống kê qua các thời kì.

Thời kì cộng sản nguyên thuỷ: Thời kì này chưa có sản xuất, chưa có sở hữu tư nhân về tư liệu sản xuất, của cải do thiên nhiên cung cấp và là của chung, loài người chưa có tính toán, nên chưa có nhu cầu về thống kê.

Thời kì chiếm hữu nô lệ: Thời kì này, có sở hữu tư nhân về tư liệu sản xuất nên đã bắt đầu có những ghi chép, tính toán những tài sản thuộc quyền chiếm hữu như ruộng đất, trâu bò, nhà cửa... Thực tế có di tích cổ mà người ta đã tìm thấy ở Trung Quốc, Hy Lạp, Ai Cập, La Mã... thì những ghi chép và tính toán này còn đơn giản, mang tính chất cộng dồn, trong phạm vi hẹp. Có thể nói rằng đó mới là công việc sơ khai của thống kê.

Thời kì phong kiến: Thời kì này, sản xuất phát triển hơn, sản phẩm nhiều hơn, phạm vi chiếm hữu tư liệu sản xuất mở rộng hơn nên yêu cầu tính toán nhiều hơn và phức tạp hơn. Theo Desrosières, A. (1998) cho biết, các nước ở châu Âu, châu Á đã tổ chức việc đăng kí kê khai về ruộng đất, nhân khẩu, tài sản... Những công việc này đã thể hiện tính chất thống kê. Sản xuất nông nghiệp ngày càng phát triển, sản phẩm dồi dào dẫn đến nhu cầu trao đổi hàng hoá, các ngành nghề thủ công ra đời... Từ đó, công việc ghi chép mở rộng ra ngoài lĩnh vực mỗi ngành, nhưng thống kê học chưa được hình thành.

Thời kì tư bản chủ nghĩa cũ: Thời kì này, lực lượng sản xuất phát triển hơn, các ngành sản xuất mới ra đời, công nghiệp, giao thông vận tải, thương nghiệp... Các hoạt động kinh tế xã hội ngày càng phức tạp hơn, sự phân công lao động xã hội cũng phát triển. Để phục vụ cho giai cấp thống trị, đòi hỏi phải theo dõi mọi mặt của xã hội (kinh tế, chính trị). Người ta đã đi sâu nghiên cứu về lí luận và phương pháp thu thập, tính toán các tài liệu sao cho phản ánh đúng hiện tượng và giúp cho người làm công tác quản lí kinh tế, quản lí xã hội điều hành tốt các công việc của mình.

Cuối thế kỉ 17, một số tài liệu sách báo của thống kê được xuất bản hoặc một số trường đã bắt đầu giảng môn lí luận thống kê. Ở thời kì này, sự phát triển của toán học, nhất là lí thuyết xác suất cũng rất mạnh mẽ đã góp phần trang bị thêm phương pháp tính toán và quản lí công việc của các nhà thống trị. Thống kê đã bắt đầu được hình thành.

Ngay đầu thế kỉ XX, nhà khoa học người Anh, Oen (Well, H.G.) đã dự báo như sau: “Trong một tương lai không xa, kiến thức thống kê và tư duy thống kê sẽ trở thành một yếu tố không thể thiếu được trong học vấn phổ thông của mỗi công dân, giống như là khả năng biết đọc biết viết vậy” (sách giáo khoa-10-NC, trang 159).

Ngày nay, do sự phát triển của xã hội loài người, do sự tiến triển của khoa học kĩ thuật, khoa học thống kê cũng ngày càng hoàn thiện về lí luận và phương pháp. Thống kê chính là một công cụ mạnh mẽ nhất để nhận thức xã hội. Thống kê ngày càng trở nên quan trọng trong đời sống, trong phát triển kinh tế - xã hội, trong giáo dục, an ninh quốc phòng và nhận thức thế giới.

3.2. Biểu đồ cột và biểu đồ histogram

3.2.1. Biểu đồ cột

Biểu đồ hình cột được sử dụng để biểu diễn trực quan thông tin của các biến định tính hoặc định lượng rời rạc, bao gồm các cột có chiều rộng bằng nhau, được phân tách bằng các khoảng nhỏ bằng nhau. Điểm chính yếu trong biểu đồ hình cột là việc xây dựng các cột ứng với các giá trị khác nhau của biến quan sát. Các cột có thể được vẽ theo chiều đứng hoặc chiều ngang, tương ứng với mỗi giá trị khác nhau của biến đang xem xét. Chiều cao (hoặc chiều dài) của mỗi cột biểu diễn tần số hay tuần suất của mỗi “lớp”.

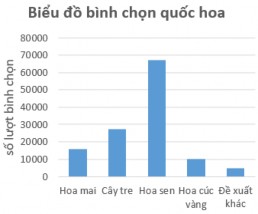
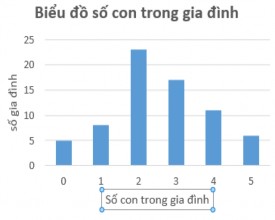
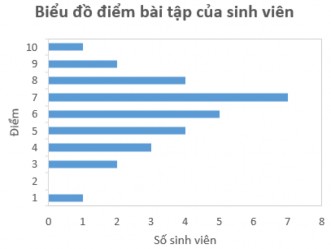
Hình 3.1. Minh họa biểu đồ cột

3.2.2. Biểu đồ histogram

Biểu đồ histogram là biểu đồ gồm các hình chữ nhật liền nhau, được dùng để biểu diễn một cách hữu ích các tập dữ liệu có kích thước lớn. Trong trường hợp dữ liệu nghiên cứu thu được có quá nhiều giá trị khác nhau (nhất là trong trường hợp biến định lượng liên tục), người ta buộc phải tìm cách nhóm các giá trị khác nhau lại thành các lớp ghép. Dựa vào độ rộng của các lớp ghép, biểu đồ histogram được phân thành hai trường hợp như sau:

• Trường hợp biểu đồ histogram có độ rộng các khoảng dữ liệu bằng nhau:

Trên mỗi khoảng dữ liệu Cita vẽ một hình chữ nhật có chiều cao bằng tần số ni

(hoặc tần suất

fi ) tương ứng của lớp ghép đó. Lưu ý rằng khi các lớp có chiều rộng

bằng nhau, tần số, tần suất và mật độ tỉ lệ với nhau.

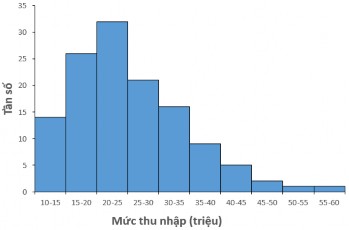
Hình 3.2. Minh họa biểu đồ histogram

• Trường hợp biểu đồ histogram có độ rộng các khoảng dữ liệu không bằng nhau: Trong trường hợp này, khi vẽ biểu đồ các cột có độ dài là độ dài của các khoảng dữ liệu li, chiều cao của các cột biểu diễn lớp thứ i được xác định theo

công thức:

h ni ,

trong đó

ni là tần số thứ i ,

li là độ dài của khoảng xác định

lớp thứ i và là hằng số dương tùy chọn. Nếu chọn

 1

thì diện tích của cột

chính bằng tần số của lớp đó. (Đặng Hùng Thắng, 2008, tr 16).

Biểu đồ histogram biểu diễn chiều cao của 400 c

ây

Hình 3.3. Minh họa biểu đồ histogram

Biểu đồ histogram biểu diễn tần số, tần suất thông qua diện tích chứ không phải thông qua chiều cao của các cột dữ liệu. Vì vậy, biểu đồ histogram không cần thang đo đứng. Để thuận tiện cho việc vẽ biểu đồ và xác định diện tích hình chữ nhật, biểu đồ histogram thường được vẽ thêm trục đứng nhưng chiều cao của các cột (đo theo trục đứng) không biểu diễn tần số, tần suất mà biểu diễn tỉ số giữa tần số, tần suất và độ rộng của lớp ghép được gọi là thang đo mật độ (Navidi, 2011). Ở

chương trình giáo dục phổ thông và chương trình đào tạo GV, biểu đồ histogram thường được trình bày ở trường hợp các khoảng dữ liệu được chia đều nhau, yếu tố diện tích chưa được đề cập rõ ràng nên rất dễ dẫn đến sự nhẫm lẫn cho người học về biểu đồ histogram và biểu đồ cột. Theo Cobb và Lock (được trích dẫn trong delMas et al., 2005), sự hiểu biết về biểu đồ histogram là một thành phần thiết yếu cần thiết cho sinh viên để phát triển sự hiểu biết về đường cong mật độ. Theo họ, biểu đồ histogram là biểu diễn đồ họa duy nhất sử dụng diện tích để biểu thị tỉ lệ và do đó, cách rõ ràng nhất để thực hiện chuyển đổi sang mật độ như một mô hình lí tưởng của biểu đồ histogram (delMas et al., 2005). Sự hiểu biết về mối liên hệ giữa biểu đồ histogram và hàm mật độ hoặc phân phối là cần thiết để hiểu phân phối lấy mẫu, từ đó, là nền tảng cho sự hiểu biết về suy luận thống kê (Madden, 2011; Meletiou- Mavrotheris & Lee, 2002).

3.2.3. Những nhầm lẫn thường gặp giữa biểu đồ cột và biểu đồ histogram

Biểu đồ cột và biểu đồ histogram là các công cụ thống kê cốt lõi, thường được coi là công cụ biểu thị dữ liệu phổ biến và được sử dụng rộng rãi trong thực tiễn thống kê hay được dạy trong các khóa học giới thiệu thống kê. Mặc dù tầm quan trọng của chúng đã được khẳng định nhưng vẫn có nhiều HS thể hiện sự hiểu lầm khi được yêu cầu đọc và giải thích các biểu đồ cột và biểu đồ histogram (Whitaker, D., và Jacobbe, T., 2017). Sự hiểu biết của HS về biểu đồ cột và biểu đồ histogram là chủ đề của nhiều nghiên cứu trong các bối cảnh khác nhau. Các nghiên cứu này đã chỉ ra rằng biểu đồ cột có thể sử dụng được đối với HS tiểu học (English, 2013), HS cấp hai (McClain, K., Cobb, P., & Gravemeijer, K., 2000; Bakker & Gravemeijer, 2004), HS trung học (delMas, Garfield & Ooms, 2005) và sinh viên đại học (delMas et al., 2005). Mặc dù biểu đồ cột thường được HS hiểu và có thể sử dụng, nhưng các nghiên cứu về sự hiểu biết của HS về biểu đồ histogram đã cho thấy nhiều hiểu lầm và nhiều lĩnh vực nhầm lẫn.

Một loạt những hiểu lầm đã được các nhà nghiên cứu xác định. Trong số những hiểu lầm phổ biến được đề cập về biểu đồ cột và biểu đồ histogram là độ phân tán của dữ liệu được biểu thị trong biểu đồ histogram bằng sự thay đổi về độ cao của các thanh. Theo Cooper, L. L., & Shore, F. S. (2010), quan niệm sai lầm về biểu đồ histogram có hình dạng bằng phẳng cho thấy ít biến thiên hơn so với biểu đồ

histogram có hình dạng gập ghềnh (không bằng phẳng). Điều này cũng phù hợp với quan niệm sai lầm về sự nhầm lẫn xem chiều cao của các cột trong biểu đồ histogram biểu diễn giá trị như biểu đồ cột. Một sự hiểu lầm khác đã được chứng minh là “biểu đồ cột hình chuông có thể biểu thị sự phân bố của một biến định lượng,” được đề cập trong nghiên cứu của delMas và cộng sự (2007, trang 46). Kaplan và cộng sự (2014) cũng nhận thấy rằng sinh viên bị nhầm lẫn giữa trục ngang và trục dọc (tức là nhầm lẫn giữa tần số và giá trị dữ liệu) và hiểu lầm rằng biểu đồ histogram bằng phẳng hơn thể hiện sự biến thiên ít hơn. Cuối cùng, delMas và cộng sự (2005) nhận thấy rằng sinh viên dường như gặp khó khăn khi đọc biểu đồ histogram và biểu đồ cột khi các cột biểu thị các khoảng chứ không phải các giá trị đơn lẻ.

Dựa vào những kết quả trong các nghiên cứu phân tích ở trên, chúng tôi nhận thấy rằng nhiều GVTTL sẽ không chắc chắn với sự khác biệt giữa biểu đồ thanh và biểu đồ histogram và thường có những hiểu lầm về bản chất của hai loại biểu đồ này. Từ đó, sẽ dẫn đến nhiều sự sai lầm tiếp theo trong phân tích dữ liệu thống kê như xác định các số đặc trưng đo xu thế trung tâm, so sánh độ phân tán của dữ liệu hay ảnh hưởng đến tư duy thống kê…Vì vậy, ở phần sau, chúng tôi chọn hai loại biểu đồ cột và biểu đồ histogram làm đối tượng nghiên cứu trong thực nghiệm.

3.3. So sánh các số đặc trưng đo xu thế trung tâm dựa trên hình dạng phân bố của biểu đồ

Ở phần này chúng tôi so sánh các số đặc trưng đo xu thế trung tâm là trung bình, trung vị và mốt. Vậy trong ba giá trị đó, giá trị nào là thích hợp và nên sử dụng để đại diện cho xu thế trung tâm? Câu trả lời cho câu hỏi này phụ thuộc vào loại dữ liệu và phân bố của các dữ liệu quan sát. Tuy nhiên, có thể nói rằng không có số đo thống kê nào trên đây là hoàn hảo trong việc mô tả một vị trí trung tâm của một phân bố. Với biến định tính thì chỉ có thể dùng một loại duy nhất đó là mốt (Dương Thiệu Tống, 2005).

Về mặt lí thuyết, giá trị trung bình thường được dùng làm giá trị đại diện cho xu hướng trung tâm của phân bố vì ba lí do:

+ Giá trị trung bình có thể tính toán được từ các dữ liệu số, sử dụng hết tất cả các số liệu thu thập được và là đơn nhất trong một mẫu số liệu.

+ Giá trị trung bình là số đo lường khuynh hướng định tâm một cách vững chãi nhất vì nó ít biến thiên nhất từ mẫu số liệu này sang mẫu số liệu khác. Ngoài ra, trong một phân bố dữ liệu có thể có một hay nhiều mốt.

+ Giá trị trung bình được sử dụng trong nhiều thao tác tính toán về sau, đó là điều không thể thực hiện được với trung vị và mốt. Mặt khác, trung bình được sử dụng cho nhiều sự so sánh thống kê, trong khi đó trung vị và mốt sẽ được ít nhắc đến hơn.

Trung bình chịu ảnh hưởng của các giá trị ngoại vi, còn trung vị thì không bị ảnh hưởng của các giá trị đó. Tuy nhiên, trung vị là một trung bình vị trí và không đơn nhất. Mốt của một tập dữ liệu có thể có một giá trị, nhiều giá trị hoặc không có giá trị nào, dễ dàng để xác định và không bị ảnh hưởng bởi các giá trị ngoại lai. Trong tập dữ liệu biến định tính, mốt được sử dụng làm giá trị đại diện cho xu hướng tập trung của dữ liệu.

Nếu sự phân bố của một tập hợp dữ liệu là đối xứng thì giá trị trung bình, trung vị và mốt là như nhau (hoặc là xấp xỉ nhau). Nếu phân bố lệch về phía trái thì trung bình nhỏ hơn trung vị. Ngược lại, nếu phân bố lệch về phía phải thì trung bình lớn hơn trung vị.

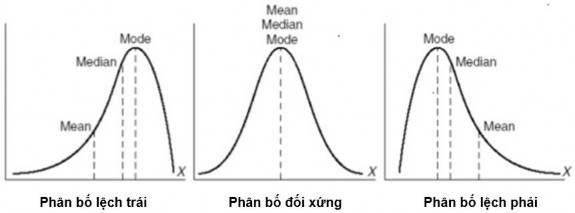
Hình 3.4. Vị trí tương đối của trung bình, trung vị, mốt dựa vào phân bố của dữ liệu (Dương Thiệu Tống, 2005)

Dựa vào vị trí tương đối của trung bình, trung vị, mốt ta có thể so sánh các giá trị mà không cần phải tính toán các giá trị cụ thể. Từ đây cho chúng ta có thể lựa chọn giá trị đại diện nào phù hợp cho xu hướng trung tâm đối với từng phân bố và đưa ra những nhận định có ý nghĩa.

3.4. Kiến thức của giáo viên để dạy học biểu đồ cột và biểu đồ histogram trong thống kê

Để vận dụng mô hình MKT vào đánh giá kiến thức của GV để dạy học biểu đồ cột và biểu đồ histogram, chúng tôi xây dựng bộ chỉ số đánh giá các kiểu kiến thức dựa trên đặc trưng của mỗi kiểu kiến thức trong mô hình MKT và nội dung dạy học biểu đồ cột và biểu đồ histogram như sau:

Bảng 3.1. Bộ chỉ số đánh giá các kiểu kiến thức để dạy học biểu đồ cột và biểu đồ histogram

Kiểu kiến thức

Các biểu hiện
A: Các chỉ số liên quan đến kiểu kiến thức nội dung phổ biến (CCK)	CCK11: GV hiểu được khái niệm, bản chất của biểu đồ cột, biểu đồ histogram, xác định được các trường hợp của biểu đồ cột, biểu đồ histogram; biểu diễn mối liên hệ giữa các dữ liệu thu thập với dữ liệu mô tả trên biểu đồ cột, biểu đồ histogram một cách chính xác. CCK12: GV có thể hiểu được ý nghĩa của biểu đồ cột, biểu đồ histogram trong biểu diễn dữ liệu và vận dụng vào các bài toán hay tình huống có bối cảnh thực tế, phân biệt được sự khác nhau giữa biểu đồ histogram và biểu đồ cột.
B: Các chỉ số liên quan đến kiểu kiến thức đặc thù (SCK)	SCK11: GV có khả năng biểu đạt các đặc trưng của biểu đồ cột, biểu đồ histogram một cách đầy đủ và chính xác thông qua các hoạt động dạy học như dự đoán được các câu trả lời mà HS có thể đưa ra và lí do vì sao HS lại trả lời như vậy. SCK12: GV có khả năng bình luận, phân tích tính đúng/sai trong các tài liệu và các lời giải mà HS đưa ra bằng cách cung cấp các giải thích về các bước lập luận trong câu trả lời liên quan đến biểu đồ cột, biểu đồ histogram một cách rõ ràng.
C: Các chỉ số liên quan đến kiểu kiến thức theo chiều ngang (HCK)	HCK11: GV có khả năng xác định câu trả lời của HS có liên quan đến kiến thức về biểu đồ cột, biểu đồ histogram hay đánh giá ý tưởng liên quan đến các biểu đồ này của bài toán đặt ra. HCK12: GV có khả năng hiểu biết biểu đồ cột, biểu đồ histogram có mối liên hệ với các mạch kiến thức, chủ đề toán trong chương trình như thế nào và nó hữu ích như thế nào đến việc sử dụng biểu đồ cột, biểu đồ histogram trong cuộc sống.