Tổng Quan Nghiên Cứu Về Kiến Thức Của Giáo Viên Để Dạy Học

Ngoài phần Mở đầu, luận án được chia làm 6 chương:

Trong chương 1, chúng tôi phân tích các nghiên cứu liên quan đến kiến thức toán để dạy học và năng lực nghề nghiệp của GV toán, đặc biệt là các nghiên cứu dựa trên mô hình của Ball và cộng sự (2008); tổng quan các nghiên cứu về kiến thức của GV để dạy học thống kê. Bên cạnh đó, chúng tôi phân tích đặc trưng tri thức luận và nội dung của chủ đề thống kê ở phổ thông cũng như trong chương trình đào tạo GV toán, làm cơ sở để phát triển, điều chỉnh mô hình kiến thức toán để dạy học của Ball và cộng sự (2008) vào ngữ cảnh dạy học thống kê.

Trong chương 2, chúng tôi trình bày chi tiết mô hình các kiểu kiến thức toán của Ball và cộng sự (2008). Cụ thể, chúng tôi phân tích rõ từng thành phần kiến thức của mô hình MKT và đề cập đến một số nghiên cứu về mô hình kiến thức thống kê để dạy học. Tiếp theo đó, chúng tôi giới thiệu NCBH và một số nghiên cứu phát triển nghiệp vụ cho GV theo NCBH.

Trong chương 3, chúng tôi sơ lược tri thức luận và lịch sử thống kê và trình bày một số kiến thức cơ sở về biểu đồ cột và biểu đồ histogram, các số đặc trưng đo xu thế trung tâm và độ phân tán của dữ liệu trên biểu đồ cột và biểu đồ histogram. Bên cạnh đó chúng tôi xây đựng các bộ chỉ số nhằm đánh giá kiến thức của GV để dạy học biểu đồ thống kê, các số đặc trưng đo xu thế trung tâm và độ phân tán của dữ liệu trên biểu đồ thống kê. Phần cuối chương, mục tiêu cụ thể của nghiên cứu được chúng tôi đặt ra và cụ thể hóa thành những câu hỏi nghiên cứu.

Nội dung chương 4 trình bày chi tiết phương pháp nghiên cứu của luận án. Cụ thể, chúng tôi nêu ngữ cảnh các thực nghiệm; mục tiêu và phương pháp nghiên cứu; quy trình thực nghiệm và thu thập dữ liệu; công cụ nghiên cứu, phân tích tiên nghiệm phiếu khảo sát và cách thức phân tích dữ liệu thực nghiệm.

Chương 5 trình bày kết quả nghiên cứu của thực nghiệm. Ở đây, chúng tôi tập trung vào phân tích bốn kiểu kiến thức là kiến thức nội dung phổ biến, kiến thức nội dung đặc thù, kiến thức về việc học của học sinh và kiến thức về việc dạy của các GVTTL trong từng thực nghiệm và mô tả sự tiến triển kiến thức của họ khi tham gia NCBH.

Chương 6, từ kết quả nghiên cứu, chúng tôi trình bày các phân tích sâu và lí giải cho các kết quả thu được ở chương 5 nhằm trả lời cho các câu hỏi nghiên cứu đặt ra. Bên cạnh đó, chúng tôi thảo luận về những đóng góp của nghiên cứu và khả năng ứng dụng các kết quả của nghiên cứu trong đào tạo GV.

CHƯƠNG 1

ĐẶT VẤN ĐỀ NGHIÊN CỨU

Có thể bạn quan tâm!

Xem toàn bộ 277 trang tài liệu này.

Trong chương này, chúng tôi trình bày các nghiên cứu liên quan đến các kiểu kiến thức toán để dạy học là bản chất của năng lực nghề nghiệp của GV toán, đặc biệt là các nghiên cứu dựa trên mô hình của Ball và cộng sự (2008). Đi sâu hơn nữa, việc tổng quan các nghiên cứu về kiến thức của GV để dạy học thống kê cho chúng tôi hiểu rõ hơn các đặc trưng của các kiểu kiến thức khi áp dụng trong dạy học thống kê. Bên cạnh đó chúng tôi phân tích nội dung của chủ đề thống kê ở phổ thông cũng như trong chương trình đào tạo GV toán, làm cơ sở để phát triển, điều chỉnh mô hình kiến thức toán để dạy học của Ball và cộng sự (2008) vào ngữ cảnh dạy học thống kê.

1.1. Tổng quan nghiên cứu về kiến thức của giáo viên để dạy học

Nghiên cứu về kiến thức của GV để dạy học là một lĩnh vực quan trọng trong đào tạo và phát triển nghiệp vụ cho GV. Kiến thức nội dung và kiến thức nội dung sư phạm đã được coi là những thành phần cốt lõi của năng lực GV (Ball, Thames & Phelps, 2008; Shulman, 1987). Các nghiên cứu gần đây cho thấy rằng kiến thức nội dung và kiến thức nội dung sư phạm tác động đến chất lượng giảng dạy và sự tiến bộ của học sinh (HS) (Fennema & Franke, 1992; Ball, Thames & Phelps, 2008; Hill, Ball & Schilling, 2008; Baumert et al., 2010; Petrou & Goulding, 2011). Trong suốt quá trình nghiên cứu giáo dục, các nhà nghiên cứu đã làm việc để mô tả kiến thức mà GV cần để giảng dạy cũng như cách GV có thể phát triển loại kiến thức này. Ở phần tiếp theo, chúng tôi trình bày một số công trình của các nhà nghiên cứu có ảnh hưởng lớn trên thế giới như công trình của Shulman (1986), Fennema và Franke (1992), Rowland và cộng sự (2003, 2005, 2007), Ball và cộng sự (2008) là cơ sở nền tảng kiến thức cho nghiên cứu của chúng tôi.

1.1.1. Nghiên cứu của Shulman

Trong lĩnh vực này, Shulman (1986) được xem là nhà nghiên cứu tiên phong mở đường cho các nghiên cứu về kiến thức của GV cần thiết cho việc giảng dạy. Shulman cho rằng trước đó có ít nghiên cứu liên quan đến vai trò của kiến thức nội dung của GV ảnh hưởng đến việc dạy học của họ, trọng tâm của các nghiên cứu trước đây chỉ xoay quanh các tiến trình, cách thức dạy học mà bỏ lỡ các nghiên cứu về kiến thức nội dung giảng dạy. Chương trình nghiên cứu của Shulman đã cho thấy kiến thức của GV là yếu

tố rất quan trọng ảnh hưởng nhiều đến thực hành dạy học của họ và các hình thức hành vi của GV thúc đẩy hiệu quả đến thành tích học tập của HS (Shulman, 1986). Những câu hỏi nghiên cứu như GV quyết định về những nội dung cần dạy như thế nào? Làm thế nào để biểu đạt những nội dung cần dạy đó? Làm thế nào để giải quyết những sai lầm của HS về nội dung toán học nào đó?... là trọng tâm chú ý của Shulman và những nghiên cứu hướng đến các kiểu kiến thức cần có của GV.

Theo Petrou và Goulding (2011), Shulman đã đề xuất phân loại các kiểu kiến thức của GV thành bảy loại như sau: kiến thức sư phạm tổng quát, kiến thức về đặc điểm của người học, kiến thức về ngữ cảnh dạy học, kiến thức về mục tiêu và giá trị giáo dục, kiến thức nội dung môn học, kiến thức nội dung sư phạm và kiến thức chương trình. Tuy nhiên, Shulman chỉ tập trung vào kiến thức liên quan trực tiếp đến nội dung toán học được dạy. Vì vậy, bốn kiểu kiến thức đầu tiên đề cập đến các khía cạnh tổng quát của kiến thức của GV và đó không phải là trọng tâm của các nghiên cứu của Shulman. Ba kiểu kiến thức còn lại, là kiến thức nội dung môn học, kiến thức chương trình và kiến thức nội dung sư phạm liên quan trực tiếp đến những khía cạnh nội dung toán của kiến thức GV, là những vấn đề còn chưa được chú ý đúng mức trong nghiên cứu về dạy học. Trong nghiên cứu của mình, Shulman đã tập trung phân tích ba kiểu kiến thức:

• Kiến thức nội dung môn học (Subject Matter Knowledge) bao gồm kiến thức về các chủ đề dạy học của môn học và cách thức tổ chức, sắp xếp cấu trúc của nó. GV không chỉ cần hiểu rằng một cái gì đó là như thế nào mà cần phải hiểu rõ thêm tại sao nó lại như vậy. Shulman cho rằng kiến thức nội dung môn học phải vượt lên trên kiến thức về những khái niệm hay sự kiện của một lĩnh vực.

• Kiến thức chương trình (Curricular Knowledge) là kiến thức của người GV hiểu biết đầy đủ về chương trình giảng dạy môn học và chủ đề cụ thể ở cấp độ nhất định, sự đa dạng của các tài liệu giảng dạy liên quan đến các chương trình đó, kiến thức về những hướng dẫn giảng dạy, về sách giáo khoa, cũng như kiến thức về những chủ đề và những cách thức trong đó những chủ đề này được trình bày, hay những lưu ý cho việc sử dụng các chương trình hoặc tài liệu chương trình cụ thể trong các trường hợp cụ thể. Mặt khác, có kiến thức về chương trình tốt người GV dựa vào đó xây dựng những công cụ giảng dạy phù hợp, đồng thời đây cũng là quy chuẩn giúp GV đánh giá mức độ phù hợp thành tích học tập của HS.

• Kiến thức nội dung sư phạm (Pedagogical Content Knowledge) là kiểu kiến thức có tính mới và có ảnh hưởng nhất. Shulman (1986) quan niệm kiến thức nội dung sư phạm là tập hợp của kiến thức về nội dung và kiến thức về sư phạm đặc thù cho việc dạy học. Kiến thức nội dung sư phạm bao gồm những dạng biểu diễn đặc thù cho nội dung toán, những ví dụ và ứng dụng mà GV sử dụng để làm cho HS dễ hiểu hơn, cùng với những chiến lược dạy học để giúp HS vượt qua khó khăn. Với khái niệm kiến thức nội dung sư phạm, Shulman muốn nhấn mạnh không phải chỉ đơn thuần là kiến thức nội dung, cũng không đơn thuần là kiến thức sư phạm, mà phải là một sự kết hợp của hai kiểu kiến thức này trong dạy học. Tính hữu dụng của kiến thức nội dung sư phạm được thể hiện qua việc ngay khi được Shulman (1986) giới thiệu, nó đã được nhiều nhà nghiên cứu thích nghi, điều chỉnh, sử dụng, phát biểu lại khái niệm này. Chẳng hạn, Meredith (1995) cho rằng cần một khung nội dung rộng hơn, mở rộng của kiến thức nội dung sư phạm là cần thiết.

Cho dù công trình của Shulman (1986) là mang tính tiên phong và ảnh hưởng lớn đến lĩnh vực nghiên cứu kiến thức của GV, nhiều nhà nghiên cứu sau này đã cho rằng sự phân loại các kiểu kiến thức GV của Shulman (1986) là chưa đủ rõ và đủ để có thể thực hành trong nghiên cứu (Zhang & Stephens, 2013). Theo Ball và cộng sự (2008), sự phân biệt giữa khái niệm kiến thức nội dung và kiến thức nội dung sư phạm theo Shulman thường chưa được rõ ràng. Hơn nữa, Shulman chưa chú trọng đến sự tương tác giữa các kiểu kiến thức này (Hashweh, 2005).

1.1.2. Nghiên cứu của Fennema và Franke

Mô hình của Fennema & Franke (1992) được xây dựng nhằm sửa đổi những hạn chế trong nghiên cứu của Shulman (1986). Fennema và Franke (1992) cho rằng sự phân loại của Shulman (1986) chưa chú trọng đến bản chất động của kiến thức, mà kiến thức của GV thường phát triển qua những tương tác trong lớp học với HS liên quan đến nội dung toán học hướng đến. Bằng cách phân loại các tình huống từ các lớp học nơi kiến thức toán học xuất hiện trong giảng dạy, họ đề xuất một mô hình kiến thức cho GV được sử dụng để mô tả những gì GV cần trong giảng dạy toán học. Mô hình quan niệm về kiến thức GV của hai tác giả này dựa trên sự phân loại của Shulman (1986), nhưng tập trung hơn vào khía cạnh tương tác và động của bản chất kiến thức của GV. Họ cho rằng kiến thức toán học để giảng dạy bao gồm bốn thành phần: kiến thức về nội dung, kiến thức về sư phạm, kiến thức về nhận thức của HS và niềm tin của GV.

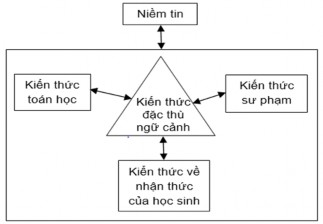
Hình 1.1. Mô hình kiến thức của giáo viên theo Fennema và Franke (1992)

Mô hình của Fennema và Franke (1992) tập trung vào kiến thức của GV khi nó xảy ra trong bối cảnh của lớp học. Trọng tâm trong quá trình hình thành khái niệm của họ nhấn mạnh đến kiến thức có bản chất tương tác và trong một bối cảnh nhất định, kiến thức về nội dung của GV có liên quan đến kiến thức về sư phạm, nhận thức của HS và kết hợp với niềm tin để tạo ra một bộ kiến thức xác định thực hành giảng dạy và hành vi của GV trong lớp học. Hơn nữa, họ cho rằng kiến thức có tính chất động và cho rằng dạy học là một quá trình trong đó GV có thể thay đổi kiến thức hiện có và tạo ra kiến thức mới.

Kiến thức nội dung toán của GV theo Fennema và Franke (1992, trang 162) bao gồm:

“kiến thức của GV về các khái niệm, quy trình và quá trình giải quyết vấn đề trong lĩnh vực mà họ giảng dạy. Nó bao gồm kiến thức về các khái niệm cơ bản của các quy trình, sự liên quan lẫn nhau của các khái niệm và cách các khái niệm và quy trình này được sử dụng trong các dạng giải quyết vấn đề khác nhau”

Thành phần kiến thức sư phạm đề cập đến “kiến thức của GV về các quy trình giảng dạy như các chiến lược hiệu quả để lập kế hoạch, các thói quen trong lớp học, kĩ thuật quản lí hành vi, quy trình tổ chức lớp học và kĩ thuật tạo động lực” (Fennema & Franke, 1992, trang 162). Từ sự hình thành khái niệm của Fennema và Franke, có thể nói rằng thành phần kiến thức sư phạm có liên quan đến phạm trù kiến thức sư phạm chung của Shulman, bao gồm các nguyên tắc và chiến lược rộng rãi về quản lí lớp học. Hơn nữa, khi xem xét kiến thức sư phạm của GV, họ thảo luận về kiến thức của GV về biểu diễn theo cách tương tự như cách hình thành khái niệm của Shulman, theo đó việc sử dụng biểu diễn là trọng tâm trong giảng dạy (Petrou & Goulding, 2011).

Fennema và Franke (1992, trang 162) đã mô tả thành phần kiến thức về nhận thức của HS bao gồm:

“kiến thức về cách HS tư duy và đặc biệt cách học nội dung toán học đó diễn ra như thế nào, cũng như hiểu biết về các quy trình mà HS sẽ sử dụng, những khó khăn và thuận lợi có thể xảy ra mà HS sẽ gặp phải”

Theo sự phân loại của Shulman (1986), kiến thức về nhận thức của HS được xem như là một phần của kiểu kiến thức sư phạm của GV. Nhưng Fennema & Franke (1992) đã xem kiểu kiến thức này là một kiểu kiến thức riêng, tách khỏi kiểu kiến thức sư phạm. Tuy vậy, một vấn đề chia sẻ chung của cả hai mô hình, đó là kiến thức về việc HS tư duy và học như thế nào là yếu tố có vai trò trung tâm của việc dạy học hiệu quả. Ý tưởng này cùng phù hợp với những nghiên cứu về sau.

Trong mô hình của Fennema và Franke (1992), tất cả các khía cạnh của kiến thức và niềm tin của GV có liên quan đến nhau, và tất cả đều phải được xem xét để hiểu được việc giảng dạy toán học. Họ gợi ý rằng không có một lĩnh vực kiến thức nào của GV có vai trò duy nhất trong việc giảng dạy toán học hiệu quả. Do đó, đối với Fennema và Franke (1992), thách thức của nghiên cứu trong lĩnh vực kiến thức GV là phát triển phương pháp luận với mục đích hiểu được sự tương tác giữa các loại kiến thức khác nhau của GV, vai trò của chúng trong việc giảng dạy toán học (Petrou & Goulding, 2011).

1.1.3. Mô hình kiến thức chủ đề trong toán học

Dự án của trường đại học Cambridge có tiêu đề “Kiến thức chủ đề về toán học” (Rowland, 2005; Rowland, 2007; Rowland, Huckstep, & Thwaites, 2003) điều tra mối quan hệ giữa kiến thức chủ đề môn học của GV tương lai và kiến thức nội dung sư phạm của họ về toán học. Kết quả của dự án này đã xác định được một khung lí thuyết gọi là Bộ tứ kiến thức (Knowledge Quartet) bao gồm bốn khía cạnh: nền tảng, chuyển đổi, kết nối và thích ứng. Không đi vào cụ thể hoá sự phân loại kiến thức của GV như Shulman (1986), khung lí thuyết “Bộ tứ kiến thức” đáp ứng cho mô hình của Fennema và Franke (1992) bằng cách phân loại các tình huống trong lớp học ở đó kiến thức toán xuất hiện trong dạy học. Mô hình này bao gồm các thành tố:

• Nền tảng (Foundation) bao gồm kiến thức, niềm tin và sự hiểu biết của HS có được để chuẩn bị cho vai trò của họ trong lớp học. Các thành phần quan trọng của nền tảng lí thuyết này là: kiến thức và hiểu biết về toán học theo từng

ngành và kiến thức về các khía cạnh quan trọng của tài liệu về việc dạy và học toán học, cùng với niềm tin về bản chất của kiến thức toán học, mục đích của giáo dục toán học và điều kiện mà học sinh sẽ học toán tốt nhất.

• Chuyển đổi (Transformation) liên quan đến kiến thức trong hành động như đã được thể hiện trong cả việc lập kế hoạch giảng dạy và trong chính hành động giảng dạy, bao gồm các kiểu biểu diễn và ví dụ được sử dụng trong hành động khi dạy học bởi GV cũng như các giải thích của GV và các câu hỏi được hỏi từ HS.

• Kết nối (Connection) là sự gắn kết những lựa chọn và quyết định đã được thảo luận rời rạc nhằm hiểu biết sâu sắc về toán học cơ bản, bao gồm các liên kết được thực hiện giữa các bài học khác nhau, giữa các ý tưởng toán học khác nhau và giữa các phần khác nhau của một bài học. Tính kết nối cũng bao gồm việc sắp xếp thứ tự các hoạt động dạy học, hiểu biết về các khó khăn và chướng ngại mà HS có thể gặp phải với các chủ đề hay nhiệm vụ toán học.

• Thích ứng (Contingency) liên quan đến sự sẵn sàng của GV để trả lời các câu hỏi của HS, để trả lời một cách thích hợp những câu trả lời sai của HS và đi chệch khỏi kế hoạch bài học của họ. Nói cách khác, nó liên quan đến sự sẵn sàng phản ứng của GV trước những tình huống trong lớp học gần như không thể dự kiến trước.

Bộ tứ kiến thức mô phỏng các cách thức mà SMK và PCK có liên quan và phát huy tác dụng trong lớp học. Trong khung lí thuyết này, tất cả các khía cạnh của kiến thức và niềm tin của GV kết hợp với nhau như một sự tổng hợp được thể hiện ra cả khi lập kế hoạch và thực hiện giảng dạy. Khung bộ tứ kiến thức này đã được áp dụng để hỗ trợ phát triển việc giảng dạy cho GV tương lai ở Anh và các nước khác. Petrou và Goulding (2011) phát triển từ kết quả nghiên cứu của Petrou (2009) cho rằng, khung lí thuyết này cung cấp một phân loại toàn diện về các mặt kiến thức toán học của các đối tượng tham gia trong các tình huống giảng dạy. Tuy nhiên, các vấn đề liên quan đến việc giải thích và sử dụng sách giáo khoa trong giảng dạy toán đã không được giải quyết trong khuôn khổ của khung này. Zhang và Stephens (2013) cũng cho rằng bộ tứ kiến thức tập trung chủ yếu về việc đào tạo GV tương lai chứ không phải trên công việc của các GV có kinh nghiệm và vẫn còn ít thay đổi về chương trình giảng dạy. Petrou và Goulding (2011) tin rằng kiến thức của GV chỉ có thể hiểu được theo các điều kiện các ngữ cảnh cụ thể mà GV làm việc. Theo đó, họ cung cấp tổ hợp mô hình Cambridge về kiến thức toán để dạy học được thể hiện trong hình 1.2.

Kiến thức chương trình (Nền tảng, chuyển đổi)

Ngữ cảnh

Kiến thức chủ đề môn học: bản chất, cú pháp, niềm tin (Nền tảng)

Kiến thức nội dung sư phạm (Chuyển đổi, kết nối, dự đoán)

Hình 1.2. Tổ hợp các mô hình kiến thức toán của giáo viên để giảng dạy theo Petrou và Goulding (2011)

Mô hình Cambridge nhấn mạnh hơn về kiến thức chương trình so với mô hình của Shulman (1986) hay mô hình MKT (Ball et al., 2008; Hill et al., 2008) và xem kiến thức chương trình giảng dạy là trung tâm trong việc hiểu những gì GV cần biết để dạy toán hiệu quả. Ngoài ra, mô hình Cambridge cũng chỉ ra rằng SMK và PCK của GV làm thay đổi cách hiểu của GV, cách họ giải thích và sử dụng chương trình toán cũng như tài liệu học tập tương ứng (Ball & Cohen, 1996; Petrou, 2009).

1.1.4. Nghiên cứu của Ball và cộng sự

Kể từ công trình có tính tiên phong của Shulman, nhiều nghiên cứu đã quan tâm đến việc phân loại và đánh giá các kiểu kiến thức khác nhau của người GV để dạy học toán hiệu quả. Trong các nghiên cứu này, có thể nói nổi bật là các nghiên cứu về kiến thức của GV để dạy học toán của Ball và cộng sự (Hill, Schilling & Ball, 2004; Ball, Thames & Phelps, 2008; Hill et al., 2008). Ball, Thames và Phelps (2008) đã có đóng góp quan trọng trong lĩnh vực nghiên cứu này bằng cách phân biệt các kiểu kiến thức khác nhau mà người GV cần có để dạy học toán hiệu quả, còn gọi là mô hình kiến thức toán để dạy học (Mathematical Knowledge for Teaching, MKT). Mô hình này làm rõ sự khác biệt giữa kiến thức nội dung môn học (Subject Matter Knowledge, SMK) và kiến thức nội dung giảng dạy (Pedagogical Content Knowledge, PCK). Cụ thể, kiến thức nội dung môn học được chia thành ba loại: kiến thức nội dung phổ biến (Common Content Knowledge, CCK), kiến thức nội dung đặc thù (Specialized Content Knowledge, SCK) và kiến thức theo chiều ngang (Horizon Content Knowledge, HCK). Kiến thức nội dung sư phạm cũng