Ứng Dụng Cây Quyết Định Trong Khai Phá Dữ Liệu

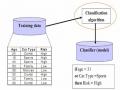
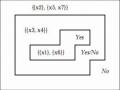
2.1.2.2. Tạo cây

Cây quyết định được tạo thành bằng cách lần lượt chia (đệ quy) một tập dữ liệu thành các tập dữ liệu con, mỗi tập con được tạo thành chủ yếu từ các phần tử của cùng một lớp.

Các nút (không phải là nút lá) là các điểm phân nhánh của cây. Việc phân nhánh tại các nút có thể dựa trên việc kiểm tra một hay nhiều thuộc tính để xác định việc phân chia dữ liệu.

2.1.2.3. Tiêu chuẩn tách

Việc lựa chọn chủ yếu trong các thuật toán phân lớp dựa vào cây quyết định là chọn thuộc tính nào để kiểm tra tại mỗi nút của cây. Chúng ta mong muốn chọn thuộc tính sao cho việc phân lớp tập mẫu là tốt nhất. Như vậy chúng ta cần phải có một tiêu chuẩn để đánh giá vấn đề này. Có rất nhiều tiêu chuẩn được đánh giá được sử dụng đó là:

+ Lượng thông tin thu thêm IG (Information Gain, thuật toán ID3 của John Ross Quilan [9]).

+ Độ phụ thuộc của thuộc tính quyết định vào thuộc tính điều kiện theo nghĩa lí thuyết tập thô của Zdzisław Pawlak [3]-[10]

Các tiêu chuẩn trên sẽ được trình bày trong các thuật toán xây dựng cây quyết định ở các phần dưới đây.

2.1.2.4. Tiêu chuẩn dừng

Đây là phần quan trọng trong cấu trúc phân lớp của cây quyết định nhằm chia một nút thành các nút con.

Chúng ta tập trung một số tiêu chuẩn dừng chung nhất được sử dụng trong cây quyết định. Tiêu chuẩn dừng truyền thống sử dụng các tập kiểm tra. Chúng ta kiểm tra cây quyết định trong suốt qúa trình xây dựng cây với tập kiểm tra và dừng thuật toán khi xảy ra lỗi. Một phương pháp khác sử dụng giá trị ngưỡng cho trước để dừng chia nút. Chúng ta có thể thay ngưỡng như là giảm nhiễu, số các mẫu trong một nút, tỉ lệ các mẫu trong nút, hay chiều sâu của cây, ...

2.1.2.5. Tỉa cây

Trong giai đoạn tạo cây chúng ta có thể giới hạn việc phát triển của cây bằng số bản tin tối thiểu tại mỗi nút, độ sâu tối đa của cây hay giá trị tối thiểu của lượng thông tin thu thêm.

Sau giai đoạn tạo cây chúng ta có thể dùng phương pháp “Độ dài mô tả ngắn nhất” (Minimum Description Length) hay giá trị tối thiểu của IG để tỉa cây

(chúng ta có thể chọn giá trị tối thiểu của IG trong giai đoạn tạo cây đủ nhỏ để cho cây phát triển tương đối sâu, sau đó lại nâng giá trị này lên để tỉa cây).

2.1.3. Phương pháp tổng quát xây dựng cây quyết định

Quá trình xây dựng một cây quyết định cụ thể bắt đầu bằng một nút rỗng bao gồm toàn bộ các đối tượng huấn luyện và làm như sau [3]:

1. Nếu tại nút hiện thời, tất cả các đối tượng huấn luyện đều thuộc vào một lớp nào đó thì cho nút này thành nút lá có tên là nhãn lớp chung của các đối tượng.

2. Trường hợp ngược lại, sử dụng một độ đo, chọn thuộc tính điều kiện phân chia tốt nhất tập mẫu huấn luyện có tại nút.

3. Tạo một lượng nút con của nút hiện thời bằng số các giá trị khác nhau của thuộc tính được chọn. Gán cho mỗi nhánh từ nút cha đến nút con một giá trị của thuộc tính rồi phân chia các các đối tượng huấn luyện vào các nút con tương ứng.

4. Nút con t được gọi là thuần nhất, trở thành lá, nếu tất cả các đối tượng mẫu tại đó đều thuộc vào cùng một lớp. Lặp lại các bước 1-3 đối với mỗi nút chưa thuần nhất.

Trong các thuật toán cơ sở xây dựng cây quyết định chỉ chấp nhận các thuộc tính tham gia vào quá trình phân lớp có giá trị rời rạc, bao gồm cả thuộc tính được dùng để dự đoán trong quá trình học cũng như các thuộc tính được sử dụng để kiểm tra tại mỗi nút của cây. Do đó trong trường hợp các thuộc tính có giá trị liên tục có thể dễ dàng loại bỏ bằng cách phân mảnh tập giá trị liên tục của thuộc tính thành một tập rời các khoảng.

Việc xây dựng cây quyết định được tiến hành một cách đệ qui, lần lượt từ nút gốc xuống tới tận các nút lá. Tại mỗi nút hiện hành đang xét, nếu kiểm tra thấy thoả điều kiện dừng: thuật toán sẽ tạo nút lá. Nút này được gán một giá trị của nhãn lớp tùy điều kiện dừng được thoả mãn. Ngược lại, thuật toán tiến hành chọn điểm chia tốt nhất theo một tiêu chí cho trước, phân chia dữ liệu hiện hành theo điều kiện chia này.

Sau bước phân chia trên, thuật toán sẽ lặp qua tất cả các tập con (đã được chia) và tiến hành gọi đệ qui như bước đầu tiên với dữ liệu chính là các tập con này.

Trong bước 3, tiêu chuẩn sử dụng lựa chọn thuộc tính được hiểu là một số đo độ phù hợp, một số đo đánh giá độ thuần nhất, hay một quy tắc phân chia tập mẫu huấn luyện.

2.1.3. Ứng dụng cây quyết định trong khai phá dữ liệu

Sau khi đã xây dựng thành công cây quyết định ta sử dụng kết quả từ mô hình cây quyết định đó. Đây là bước sử dụng mô hình để phân lớp dữ liệu hoặc rút ra các tri thức trong phương pháp khai phá dữ liệu bằng phương pháp phân lớp.

2.1.3.1. Xác định lớp của các mẫu mới

Trên cơ sở đã biết giá trị của các thuộc tính của các mẫu X1, X2, …, Xn ta xác định thuộc tính quyết định (hay phân lớp) Y của đối tượng đó (có thể dùng kỹ thuật này để nhận dạng mẫu, dự báo, …)

Cây quyết định

Dữ liệu cụ thể

Dữ liệu huấn luyện

Kết quả ?

(Sunny, True, Cool, High)

Hình 7. Mô hình phân lớp các mẫu mới

2.1.3.2. Rút ra các tri thức hay luật từ cây

Với mục đích và nhiệm vụ chính của việc khai phá dữ liệu là phát hiện ra các quy luật, các mô hình từ trong CSDL. Từ mô hình thu được ta rút ra các tri thức hay các quy luật dưới dạng cây hoặc các luật dưới dạng “If … Then…”. Hai mô hình trên là tương đương, chúng có thể được chuyển đổi qua lại giữa các mô hình đó với nhau.

Ví dụ 2.2:

Một trong các luật rút ra từ cây trong ví dụ 2.1 là

+Luật 1:

IF(Humidity: high) AND (Outlook: rainy) THEM (=>Quyết định: False)

+Luật 2:

IF(Humidity: high) AND (Outlook: sunny) THEM (=>Quyết định: False)

+Luật 3:

IF(Humidity: high) AND (Outlook: Overcast) THEN (=>Quyết định: True)

…

Từ đây ta sử dụng các luật này để hỗ trợ quá trình ra các quyết định, dự đoán, …

2.2. Thuật toán xây dựng cây quyết định dựa vào Entropy

2.2.1. Tiêu chí chọn thuộc tính phân lớp

Tiêu chí để đánh giá tìm điểm chia là rất quan trọng, chúng được xem là một tiêu chuẩn “heuristic” để phân chia dữ liệu. Ý tưởng chính trong việc đưa ra các tiêu chí trên là làm sao cho các tập con được phân chia càng trở nên “trong suốt” (tất cả các bộ thuộc về cùng một nhãn) càng tốt.

Thuật toán dùng độ đo lượng thông tin thu thêm (information IG - IG) để xác định điểm chia [9]. Độ đo này dựa trên cơ sở lý thuyết thông tin của nhà toán học Claude Shannon, độ đo này được xác như sau:

Xét bảng quyết định DT = (U, C  {d} ), số giá trị (nhãn lớp) có thể của d là k. Khi đó Entropy của tập các đối tượng trong DT được định nghĩa bởi:

Entropy(U ) pi log 2 pi

i1

trong đó pi là tỉ lệ các đối tượng trong DT mang nhãn lớp i.

Lượng thông tin thu thêm (Information Gain - IG) là lượng Entropy còn lại khi tập các đối tượng trong DT được phân hoạch theo một thuộc tính điều kiện c nào đó. IG xác định theo công thức sau:



IG(U , c) Entropy(U ) | Uv |Entropy(U )

| U |v

vVc

trong đó Vc là tập các giá trị của thuộc tính c, Uv là tập các đối tượng trong DT có giá trị thuộc tính c bằng v. IG(U, c) được John Ross Quinlan [9] sử dụng làm độ đo lựa chọn thuộc tính phân chia dữ liệu tại mỗi nút trong thuật toán xây dựng cây quyết định ID3. Thuộc tính được chọn là thuộc tính cho lượng thông tin thu thêm lớn nhất.

2.2.2. Thuật toán ID3

Thuật toán ID3 – Iterative Dichotomiser 3 [9] là thuật toán dùng để xây dựng cây quyết định được John Ross Quinlan trình bày. Ý tưởng chính của thuật toán ID3 là để xây dựng cây quyết định bằng cách ứng dụng từ trên xuống (Top- Down), bắt đầu từ một tập các đối tượng và các thuộc tính của nó. Tại mỗi nút của cây một thuộc tính được kiểm tra, kết quả của phép kiểm tra này được sử dụng để phân chia tập đối tượng theo kết quả kiểm tra trên. Quá trình này được thực hiện một cách đệ quy cho tới khi tập đối tượng trong cây con được sinh ra thuần nhất theo một tiêu chí phân lớp nào đó, hay các đối tượng đó thuộc cùng một dạng giống nhau nào đó. Các lớp hay các dạng này được gọi là nhãn của nút lá của cây, còn tại mỗi nút không phải là nút lá thì nhãn của nó là tên thuộc tính được chọn trong số các thuộc tính được dùng để kiểm tra có giá trị IG lớn nhất. Đại lượng IG được tính thông qua hàm Entropy. Như vậy, IG là đại lượng được dùng để đưa ra độ ưu tiên cho thuộc tính nào được chọn trong quá trình xây dựng cây quyết định.

Giả mã của thuật toán ID3 như sau:

Dữ liệu vào: Bảng quyết định DT = (U, C  {d}) Dữ liệu ra: Mô hình cây quyết định

Function Create_tree (U, C, {d})

Begin

If tất cả các mẫu thuộc cùng nhãn lớp di then return một nút lá được gán nhãn di

else if C = null then

return nút lá có nhãn dj là lớp phổ biến nhất trong DT

else begin

bestAttribute:= getBestAttribute(U, C);

// Chọn thuộc tính tốt nhất để chia

C := C- {bestAttribute};

//xóa bestAttribute khỏi tập thuộc tính Với mỗi giá trị v in bestAttribute

begin

End

end

Uv := [U]v ;

//Uv là phân hoạch của U theo thuộc tính

//bestAttribute có giá trị là v ChildNode:=Create_tree(UV, C, {d});

//Tạo 1 nút con

Gắn nút ChildNode vào nhánh v;

Giả mã của hàm getBestAttribute như sau:

Dữ liệu vào: Bảng quyết định DT = (U, C{d})

Dữ liệu ra: Thuộc tính điều kiện tốt nhất

Function getBestAttribute (U, C);

Begin

maxIG := 0; Với mỗi c in C begin

tg : = IG(U, c);

// Tính lượng thông tin thu thêm IG(U,c)

If (tg > max IG) then begin

end

return kq;

end

maxIG := tg; kq := c;

//Hàm trả về thuộc tính có lượng thông tin thu thêm IG là lớn nhất

End

2.2.3. Ví dụ về thuật toán ID3

Xét bảng quyết định DT = {U, C  {d}} sau đây:

Outlook	Windy	Temp	Humidity	d
1	overcast	true	cool	high	True
2	sunny	false	mild	high	false
3	sunny	false	hot	high	false
4	overcast	false	hot	normal	false
5	sunny	true	hot	low	True
6	rainy	false	mild	high	false
7	rainy	false	hot	high	false
8	rainy	false	hot	normal	false
9	overcast	true	hot	low	True
10	rainy	false	mild	normal	True
11	rainy	true	hot	normal	false
12	rainy	false	hot	high	false