Một Bảng Quyết Định Với C={Age, Lems} Và D={Walk}

phân cụm dữ liệu còn có thể được sử dụng như một bước tiền xử lý cho các thuật toán khai phá dữ liệu khác.

1.3.3. Luật kết hợp (Association Rules)

Luật kết hợp là luật mà trong đó phản ánh mối quan hệ kết hợp chặt chẽ trong một tập các đối tượng trong một CSDL [2].

Mục tiêu của phương pháp này là phát hiện và đưa ra mối liên hệ giữa các giá trị dữ liệu trong CSDL. Mẫu đầu ra của giải thuật khai phá dữ liệu là tập luật kết hợp tìm được. Khai phá luật kết hợp được thực hiện qua 2 bước:

 Bước 1: Tìm tất cả các tập mục phổ biến, một văn bản phổ biến được xác định qua độ hỗ trợ và thỏa mãn độ hỗ trợ cực tiểu.

 Bước 2: Sinh ra các luật kết hợp mạnh từ tập mục phổ biến, các luật phải thỏa mãn độ hỗ trợ cực tiểu và độ tin cậy cực tiểu.

1.4. Lý thuyết tập thô

Lý thuyết tập thô (rough set theory) lần đầu tiên được đề xuất bởi Z.Pawlak vào những năm đầu thập niên 1980. Phương pháp này đóng vai trò hêt sức quan trọng trong lĩnh vực trí tuệ nhân tạo và các ngành liên quan đến nhận thức, đặc biệt là trong lĩnh vực học máy, thu nhận tri thức, phân tích quyết định, phát hiện và khám phá tri thức từ cơ sở dữ liệu, các hệ chuyên gia, các hệ hỗ trợ quyết định, lập luận dựa trên quy nạp [1]-[8].

Các lĩnh vực ứng dụng trong tập thô bao gồm:

- Chẩn đoán y học (medical diagnosis)

- Nghiên cứu dược lý ((pharmacology)

- Dự đoán thị trường cổ phiếu và phân tích dữ liệu tài chính

- Kinh doanh tiền tệ (banking)

- Nghiên cứu thị trường

- Các hệ thu nhận và lưu trữ thông tin

- Nhận dạng mẫu, gồm nhận dạng tiếng nói và chữ viết tay

- Thiết kế hệ điều khiển ( control system design)

- Xử lý ảnh (image processing)

- Thiết kế logic số(digital logic design)

Sau đây chúng ta sẽ nghiên cứu các khái niệm cơ bản của lý thuyết tập thô. Đây là những kiến thức quan trọng cho việc áp dụng tập thô để xây dựng cây quyết định.

1.4.1. Hệ thông tin

Trong hầu hết các hệ quản trị cơ sở dữ liệu thông thường thì thông tin thường được biểu diễn dưới dạng các bảng, trong đó mỗi bảng biểu diễn thông tin về một đối tượng, mỗi cột biểu diễn thông tin về một thuộc tính của đối tượng. Từ đầu những năm 80 Pawlak đã định nghĩa một khái niệm mới là hệ thông tin (infomation system) dựa trên khái niệm bảng truyền thống như sau [4]:

Định nghĩa 1.1. [1]-[8] Hệ thông tin là một cặp S = (U, A) trong đó U là tập hữu hạn khác rỗng các đối tượng (được gọi là tập vũ trụ các đối tượng) và A là tập hữu hạn khác rỗng các thuộc tính. Với mọi aA ta kí hiệu Va là tập giá trị của thuộc tính a. Nếu xU và aA thì ta kí hiệu x(a) là giá trị thuộc tính a của đối tượng x.

Ví dụ 1.1. [8] Bảng dữ liệu dưới đây là một hệ thông tin với 7 đối tượng và 2 thuộc tính.

Age	LEMS
x1	16-30	50
x2	16-30	0
x3	31-45	1-25
x4	31-45	1-25
x5	46-60	26-49
x6	16-30	26-49
x7	46-60	26-49

Có thể bạn quan tâm!

• Phân tách cụm danh từ cơ sở tiếng việt sử dụng mô hình crfs - 1
• Phân tách cụm danh từ cơ sở tiếng việt sử dụng mô hình crfs - 2
• Ứng Dụng Cây Quyết Định Trong Khai Phá Dữ Liệu
• Thuật Toán Xây Dựng Cây Quyết Định Dựa Vào Độ Phụ Thuộc Của Thuộc Tính
• Thuật Toán Xây Dựng Cây Quyết Định Dựa Vào Entropy Và Độ Phụ Thuộc Của Thuộc Tính

Xem toàn bộ 68 trang tài liệu này.

Bảng 1. Hệ thông tin đơn giản

1.4.2. Bảng quyết định

Để có thể biểu diễn một dữ liệu thực tế, trong đó có những thuộc tính quyết

đinh, chúng ta xét một trường hợp đặc biệt của hệ thông tin được gọi là bảng quyết định được định nghĩa như sau:

Định nghĩa 1.2: Bảng quyết định (hệ quyết định) là một dạng đặc biệt của hệ thông tin, trong đó tập các thuộc tính A bao gồm hai tập con rời nhau là tập thuộc tính điều kiện C và tập các thuộc tính quyết định D. Như vậy bảng quyết định là một hệ thông tin có dạng DT= (U, C D) với C  D =  [1].

Ví dụ 1.2. Bảng 2 dưới đây thể hiện một bảng quyết định, trong đó tập thuộc tính điều kiện như ở Bảng 1 và thuộc tính quyết định {Walk} được thêm vào nhận hai giá trị là Yes và No [8].

Age	LEMS	Walk
x1	16-30	50	Yes
x2	16-30	0	No
x3	31-45	1-25	No
x4	31-45	1-25	Yes
x5	46-60	26-49	No
x6	16-30	26-49	Yes
x7	46-60	26-49	No

Bảng 2. Một bảng quyết định với C={Age, LEMS} và D={Walk}

Định nghĩa 1.3. Miền khẳng định

Cho bảng quyết định DT = {U,CD}. Tập POSC(D) = C( X )

X U / IND( D )

được

gọi là C-miền khẳng định của D. Nói cách khác, uPOSC(D) nếu và chỉ nếu u(C) = v(C) kéo theo u(D) = v(D) với mọi vU [1].

Một thuộc tính c  C được gọi là không cần thiết trong DT nếu POSC(D)

= POSC-{c}(D). Ngược lại, c là cần thiết trong DT.

Ta nói bảng quyết định DT = (U, C  {d}) là độc lập nếu mọi thuộc tính c  C đều cần thiết trong DT.

Định nghĩa 1.4. Xét bảng quyết định DT = (U, C {d}) và hai đối tượng x, y  U. Ta nói x và y mâu thuẫn nhau trong DT nếu x(C) = y(C) nhưng x(d) ≠ y(d) [3].

Đối tượng x được gọi là nhất quán trong DT nếu không tồn tại một đối tượng y khác mâu thuẫn với x. DT được gọi là nhất quán nếu mọi đối tượng trong xU đều là nhất quán.

1.4.3. Quan hệ không phân biệt được

Một trong những đặc điểm cơ bản của lý thuyết tập thô là dùng để lưu giữ và xử lý các dữ liệu trong đó có sự mập mờ, không phân biệt được. Trong một hệ thông tin theo định nghĩa trên cũng có thể có những đối tượng không phân biệt được.

Định nghĩa 6: Cho hệ thông tin S = (U, A). Với mỗi tập thuộc tính B  A đều tạo ra tương ứng một quan hệ tương đương, kí hiệu IND(B) [1]-[8]:

IND(B) = {(x,x’)  U2 |  a B, x(a) = x’(a) }

IND(B) được gọi là quan hệ B-không phân biệt được. Nếu (x,x’)  IND(B) thì các đối tượng x và x’ là không thể phân biệt được với nhau qua tập thuộc tính B. Với mọi đối tượng x  U, lớp tương đương của x trong quan hệ IND(B) được kí hiệu bởi [x]B là tập tất cả các đối tượng có quan hệ IND(B) với x.

Quan hệ B- không phân biệt được phân hoạch tập đối tượng U thành các lớp tương đương, kí hiệu là U/ IND(B) hay U/B, tức là U/B = {[x]P | x  U}.

Ví dụ 1.3. [8] Xét hệ thông tin cho trong Bảng 1

Xét thuộc tính B = {LEMS}, ta có phân hoạch của tập U sinh bởi quan hệ tương đương IND(B) là:

U/B = {{x1}, {x2}, {x3, x4}, {x5, x6, x7}}

Khi đó, ta nói các cặp đối tượng x3, x4 và x5, x6 là không phân biệt qua tập thuộc tính {LEMS} vì chúng thuộc cùng một lớp tương đương định bởi quan hệ IND(B).

Nếu ta xét B = {Age, LEMS}, ta có:

U/B = {{x1}, {x2}, {x3, x4}, {x5, x7},{ x6}}

Khi đó x5 và x6 là phân biệt được qua tập thuộc tính {Age, LEMS} vì chúng không thuộc cùng lớp tương đương định bởi quan hệ IND(B).

1.4.4. Xấp xỉ tập hợp

Ta thấy ở bảng 2 khái niệm Walk không thể định nghĩa rõ ràng qua 2 thuộc tính điều kiện Age và LEMS vì có x3, x4 thuộc cùng một lớp tương đương tạo bởi 2 thuộc tính Age và LEMS nhưng lại có giá trị khác nhau tại thuộc tính

Walk. Vì vậy, nếu một đối tượng nào đó có (Age,LEMS) = (31-45, 1-25) thì ta vẫn không thể biết chắc chắn giá trị của nó tại thuộc tính Walk là Yes hay No. Vì vậy, ta thấy khái niệm Walk không được mô tả rõ ràng. Tuy nhiên, căn cứ vào tập thuộc tính {Age, LEMS} ta vẫn có thể chỉ ra được chắc chắn một số đối tượng có Walk là Yes, một số đối tượng có Walk là No, còn lại là các đối tượng thuộc tính về biên của hai giá trị Yes và No, cụ thể:

 Nếu đối tượng nào có giá trị tại tập thuộc tính {Age,LEMS} thuộc tập

{{16-30, 50}, {16-30, 26-49}} thì có Walk là Yes.

 Nếu đối tượng nào có giá trị tại tập thuộc tính {Age,LEMS} thuộc tập

{{16-30, 0}, {46-60, 26-49}} thì có Walk là No.

 Nếu đối tượng nào có giá trị tại tập thuộc tính {Age,LEMS} = {31-45, 1- 25} thì có Walk là Yes hoặc No.

Chính vì vậy ta có khái niệm xấp xỉ tập hợp như sau:

Định nghĩa 1.3. [10] Cho hệ quyết định DT = (U, C D), tập thuộc tính BC, tập đối tượng XU. Chúng ta có thể xấp xỉ tập hợp X bằng cách sử dụng các thuộc tính trong B từ việc xây dựng các tập hợp B-xấp xỉ dưới và B-xấp xỉ trên được định nghĩa như sau:

B-xấp xỉ dưới của tập X: BX = {x  U | [x]B  X}

B-xấp xỉ trên của tập X: B X = {x  U | [x]B X ≠ 

Tập hợp BX là tập các đối tượng trong U mà sử dụng các thuộc tính trong B ta có thể biết chắc chắn được chúng là các phần tử của X.

Tập hợp B X là các đối tượng trong U mà sử dụng các thuộc tính trong B ta chỉ có nói rằng chúng có thể là các phần tử của X.

Tập BNB(X) = B X BX được gọi là B-biên của tập X, nó chứa các đối tượng mà sử dụng các thuộc tính của B ta không thể xác định được chúng có thuộc tập X hay không.

Tập U B X được gọi là B-ngoài của tập X, gồm những đối tượng mà sử dụng tập thuộc tính B ta biết chắc chắn chúng không thuộc tập X.

Một tập hợp được gọi là thô nếu đường biên của nó là không rỗng, ngược lại ta nói tập này là rõ.

Ví dụ 1.4. Xét hệ quyết định cho trong Bảng 2

Xét tập đối tượng X = {x U | x(Walk) = Yes} = {x1, x4, x6} và tập thuộc tính B = {Age, LEMS}. Khi đó ta có [8]:

U/B ={{x1}, {x2}, {x3, x4}, {x5, x7},{ x6}}

BX = {x U | [x]B  X} = {x1, x6}

B X = {x  U | [x]B X ≠ } = {u1, u2, u5, u7, u8}

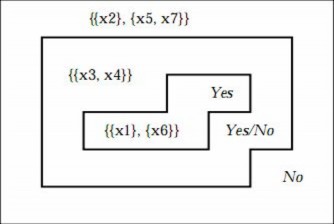
Hình 4. Xấp xỉ tập đối tượng trong Bảng 2 bởi các thuộc tính điều kiện Age và LEMS

1.5. Kết luận chương 1

+ Chương này đã giới thiệu tổng quan về khai phá dữ liệu, ứng dụng của khai phá dữ liệu, và giới thiệu một số phương pháp khai phá dữ liệu thông dụng.

+ Trình bày tổng quan về lý thuyết tập thô bao gồm hệ thống thông tin, quan hệ không phân biệt được, các tập thô, bảng quyết định,… Và đồng thời trình bày các ví dụ cụ thể để minh họa các khái niệm này.

Chương 2- CÂY QUYẾT ĐỊNH VÀ CÁC THUẬT TOÁN XÂY DỰNG CÂY QUYẾT ĐỊNH

2.1. Tổng quan về cây quyết định

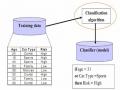
Cây quyết định là công cụ dùng để phân lớp các dữ liệu, nó có cấu trúc cây. Mỗi cây quyết định là một sự tượng trưng cho một sự quyết định của một lớp các dữ kiện nào đó. Mỗi nút trong cây là tên của một lớp hay một phép thử thuộc tính cụ thể nào đó, phép thử này phân chia không gian trạng thái các dữ kiện tại nút đó thành các kết quả có thể đạt được của phép thử. Mỗi tập con được phân chia của phép thử là không gian con của các sự kiện, nó tương ứng với một vấn đề con của sự phân lớp. Các cây quyết định được dùng để hỗ trợ quá trình ra quyết định.

2.1.1. Định nghĩa

Cây quyết định là một cây mà mỗi nút của cây là:

- Nút lá hay còn gọi là nút trả lời biểu thị cho một lớp các trường hợp mà nhãn của nó là tên của lớp.

- Nút không phải là nút lá hay còn gọi là nút trong, nút định phép kiểm tra các thuộc tính, nhãn của nút này là tên của thuộc tính và có một nhánh nối nút này đến các cây con ứng với mỗi kết quả có thể có phép thử. Nhãn của nhánh này là các giá trị của thuộc tính đó. Nút trên cùng gọi là nút gốc.

Nút gốc

Các nhánh

Nút trong

Nút trong

Nút lá

Nút lá

Hình 5. Mô tả chung về cây quyết định

Để phân lớp mẫu dữ liệu chưa biết, giá trị các thuộc tính của mẫu được đưa vào kiểm tra trên cây quyết định. Mỗi mẫu tương ứng có một đường đi từ gốc đến lá và lá biểu diễn dự đoán giá trị phân lớp của mẫu đó.

Ví dụ 2.1: Cây quyết định

Humidity

high

low

Normal

Outlook

Temp

Overcast

hot

mild

Sunn

Rainy

TRUE

FALSE

TRUE

TRUE

FALSE

FALSE

Hình 6. Ví dụ về Cây quyết định

2.1.2. Thiết kế cây quyết định

2.1.2.1. Xử lý dữ liệu

Trong thế giới thực, nói chung dữ liệu thô chắc chắn có mức độ nhiễu. Điều này có các nguyên nhân khác nhau như là dữ liệu lỗi, dữ liệu có đại lượng không chính xác, .... Do đó, chúng ta thường tiền xử lý (nghĩa là, “làm sạch”) để cực tiểu hoá hay huỷ bỏ tất cả dữ liệu thô bị nhiễu. Các giai đoạn tiền xử lý này cũng có thể biến đổi dữ liệu thô hiển thị hữu ích hơn, như hệ thống thông tin. Khi nhiều bước tiền xử lý ứng dụng hiệu quả, nó sẽ giúp cải tiến hiệu quả phân lớp.

Các công việc cụ thể của tiền xử lý dữ liệu bao gồm những công việc như:

- Filtering Attributes: Chọn các thuộc tính phù hợp với mô hình.

- Filtering samples: Lọc các mẫu (instances, patterns) dữ liệu cho mô hình.

- Transformation: Chuyển đổi dữ liệu cho phù hợp với các mô hình như chuyển đổi dữ liệu từ numeric sang nomial

- Discretization (rời rạc hóa dữ liệu): Nếu bạn có dữ liệu liên tục nhưng có một số thuật toán chỉ áp dụng cho các dữ liệu rời rạc (như ID3, ADTDA,…) thì bạn phải thực hiện việc rời rạc hóa dữ liệu.