Thuật Toán Lọc Phi Tuyến Các Thành Phần Vector Vtg Của Tbb

với các góc Ơ-le (,,) đã biết [1]. Trên cơ sở mô hình toán này có thể xây dựng và giải bài toán lọc phi tuyến các góc định hướng và các VTG theo các phép đo VTT và một cảm biến bổ sung thông tin VTG.

Trong khuôn khổ của luận án ta không thể làm sáng tỏ toàn bộ nghiệm của bài toán lọc phi tuyến theo mô hình toán duy nhất do tính chất phức tạp của chính bản thân mô hình và các thuật toán lọc tương ứng. Ta sẽ hạn chế bài toán lọc phi tuyến các VTG của TBB trong hệ TĐLK theo cách đặt bài toán trên cơ sở mô hình toán học ở chương 2.

3.1.2 Xây dựng bài toán lọc các thành phần VTG

Ta xây dựng bài toán trên cơ sở lý thuyết lọc phi tuyến.

- Kênh quan sát được mô tả bằng phương trình sau:

Với:

y(t) s(t), tntap (t)

(3.1)

- Vector y(t) là các giá trị đo, lấy từ bộ đo VTT, chúng phân bố theo các trục hệ TĐLK [ yH1x , yH1y , yH1z ], có kèm theo sai số do nhiễu tạp;

- Vector

s(t), t H1H1x , H1y , H1z T

là các giá trị đo thực của VTT

(không bị ảnh hưởng của nhiễu tạp);

- λ(t) là vector các tham số đánh giá;

- ntap (t)

là vector sai số nhiễu dạng tạp trắng có ma trận mật độ phổ

dạng đường chéo N/2



N0/2 0 0 



o  0 N0/2 0 

 0 0 N0/2

- Trong đó: Nđ/1x; Nđ/1y; Nđ/1z – mật độ phổ một phía của nhiễu đo, tương ứng với các trục. Hệ số 1/2 phản ánh mật độ phổ trên toàn dải tần số.

Do thực tế các cảm biến VTG có độ chính xác rất cao so với các cảm biến

đo từ trường và nhằm giảm kích thước và khối lượng tính toán của bài toán cần giải, ta giả sử việc bổ sung một thành phần VTG có giá trị đo đảm bảo chính xác đến mức không có sai số.

Điểm mới trong cách xây dựng bài toán cần giải chính là lựa chọn vector

đánh giá các tham số λ(t). Vector đó được mô tả như sau:

λ(t) H1x,H1y,H1z,ω1x,ω1y,ω1zT

(3.2)

Phương trình xác suất tiên nghiệm, mô tả các thành phần của vector đánh giá có dạng:

dH1x dt

1y

.H1z

1z

.H1y

dH1y

dt

1x

.H1z

1z

.H1x

(3.3)

dH1z dt

1x

.H1y

1y

.H1x

Đối với các thành phần VTG chưa biết

1x ,

1y

và 1z , cũng được mô tả

bằng các quá trình Markov bậc nhất sau đây:

d1x  1 

dt  T

1x  nht /1x

1x 

d1y 1 



1y  nht /1y

dt T1y

(3.4)



d1z  1 

dt  T

1z  nht /1z

1z 

Với:

T1x ,

T1y ,

T1z

là các hằng số thời gian của TBB;

nht /1x ,

nht /1y ,

nht /1z

là nhiễu tạp trắng tương ứng với các trục và có mật độ phổ một phía tương

ứng:

M0ht / 1x ,

M0ht /1y ,

M0ht /1z .

Thông tin bổ sung của thành phần VTG cần tổng hợp.

1y

sẽ được đưa vào thuật toán

- Yêu cầu đặt ra là cần chọn một phương án thực tế hóa vector đánh giá λ(t) nào đó, để nó có mặt trong vector quan sát và cho phép thực hiện những tính toán tiếp theo.

3.2 Thuật toán lọc phi tuyến các thành phần vector VTG của TBB

3.2.1 Mô hình toán học.

Sử dụng thuật toán lọc tĩnh cận tuyến tính để lọc phi tuyến các thành phần VTG của TBB. Khi đó, cấu trúc tối ưu của thuật toán lọc (kênh đánh giá) sẽ được khôi phục, còn các hệ số khuếch đại của kênh đánh giá được tổng hợp sẽ được chọn bằng phương pháp mô phỏng toán học kết hợp với thực nghiệm. Bằng cách như vậy, ta loại bỏ được sự cần thiết phải biết trước chính xác mật độ phổ của các loại tạp hình thành và tạp quá trình có trong các hệ số khuếch đại của kênh đánh giá. Khi các loại tạp quan sát không phụ thuộc lẫn nhau thì các phần tử nằm ngoài đường chéo chính của ma trận N và N-1 sẽ bằng không.

Dạng đặc biệt của ma trận các đạo hàm vector tín hiệu theo vector đánh giá các tham số được mô tả ở bảng 3.1:

Bảng 3.1 Dạng đặc biệt của ma trận các đạo hàm vector tín hiệu theo vector đánh giá các tham số.

Theo

H1x	H1y	H1z	ω1x	ω 1y	ω 1z
s(* , t)  	1	0	0	0	0	0
	0	1	0	0	0	0
	0	0	1	0	0	0

Có thể bạn quan tâm!

• Bản Chất Và Đặc Tính Của Sai Số Khi Đo Từ Trường Trên Thiết Bị Bay
• Phương Án Sử Dụng Duy Nhất Một Cảm Biến Vtg Độc Lập Là Con Quay Thẳng Đứng
• Phương Sai Sai Số Tổng Khi Xác Định Các Thành Phần Của Vtg
• Các Thuật Toán Lọc Phi Tuyến Khác Trong Tổng Hợp Bộ Đo Vtg Của Tbb
• Mô Phỏng Đánh Giá Các Mô Hình Hệ Thống Xác Định Vtg Đã Xây Dựng
• Nghiên cứu xác định định hướng không gian của thiết bị bay theo các phép đo từ trường trái đất - 13

Xem toàn bộ 151 trang tài liệu này.

Đơn giản hóa hơn nữa phương trình vi phân kênh đánh giá nếu chỉ giữ lại

s(* , t) 

những phép nhân với  1 khi α = μ và loại phép cộng theo μ:

i

* (t)  ai

(*, t) 



Ki

1

Y

(t)  S

(*, t)

(3.5)

Dạng cuối cùng của thuật toán lọc như sau:

dH*

* * * *

1x1y .H1z 1z .H1y  FH1x dt

dH*

1y * .H* * .H*  F

dt dH*

1x 1z

* *

1z 1x

* *

H1y

1z

dt

1x .H1y 1y .H1x  FH1z

d1x  1 *

(3.6)

dt  T

.1x  F1x

1x 



d1y 1 *

.1y  F1y

dt T1y



d1z  1 *

dt  T

.1z  F1z



Ở đây ta ký hiệu:

1z 

FH1x

 K11.YH1x (t)  H*

 K12 .YH1y (t)  H*

 K13.YH1z (t)  H*

1x

1x

FH1y  K21.YH1x (t)  H*

1x

1x

FH1z  K31.YH1x (t)  H*

 K22 .YH1y (t)  H*

1y

1y

1y

1y

 K32 .YH1y (t)  H*

 K23.YH1z (t)  H*

1z

1z

1z

1z

 K33.YH1z (t)  H*

F1x

 K41.YH1x (t)  H*

 K42 .YH1y (t)  H*

 K43.YH1z (t)  H*

(3.7)

1x

1x

F1y  K51.YH1x (t)  H* F1z  K61.YH1x (t)  H*

 K52 .YH1y (t)  H*

1y

1y

 K62 .YH1y (t)  H*

 K53.YH1z (t)  H*

1z

1z

 K63.YH1z (t)  H*

Thuật toán lọc phi tuyến (3.6), (3.7) có cấu trúc tối ưu dạng xấp xỉ Gauss. Để giảm khối lượng tính toán ở đây ta sẽ sử dụng thuật toán lọc phi tuyến cận tối ưu. Cấu trúc cận tối ưu khác với tối ưu chính là tính chất hằng số của các hệ số Ki.. Thuật toán gồm 18 hệ số như vậy, việc chọn lựa các hệ số đó sẽ được xét sau.

Trên hình 3.1 là sơ đồ cấu trúc của thuật toán. Từ sơ đồ ta thấy rõ ràng là thuật toán lọc phi tuyến là một hệ bám phi tuyến nhiều vòng. Hệ bám đó có thể quy ước phân chia thành 2 phần: phân biệt và lọc.

Phần phân biệt của thuật toán hình thành tín hiệu sai lệch F.

Phần lọc là vòng bám thứ cấp, các tín hiệu đầu ra của nó là những đánh giá các thành phần của VTT Trái đất và VTG của TBB.

Toàn bộ hệ thống được khép kín bởi một vòng hồi tiếp chính, nó bảo đảm sự so sánh trực tiếp những thành phần đầu vào của VTT y(t) đo bởi cảm biến

H

1

với những thành phần đánh giá tương ứng của vector * ở đầu ra bộ lọc.

Trong sơ đồ cấu trúc 3.1 chỉ ra những điểm vào của thông tin tiên nghiệm

từ cảm biến VTG bổ sung

1y

theo trục thẳng đứng.

Xem xét, phân tích sơ đồ cấu trúc cho phép ta đơn giản được phần phân biệt của thuật toán và cắt giảm số lượng các hệ số khuếch đại chưa biết. Các tham số đánh giá – thành phần của VTT Trái đất và vector VTG của TBB có tính chất vuông góc nhau. Tính chất đó không có cách nào thể hiện được dưới

dạng giải tích. Hơn nữa, rõ ràng rằng các giá trị đo

yH1y

và yH1z

không chứa

bất cứ thông tin nào tương ứng với thành phần vector từ trường

H1x . Vì vậy

mà các hệ số khuếch đại K12 và K13 có thể coi bằng 0 ( K12  K13  0 ).

Tương tự như vậy, có thể kết luận rằng

y không chứa thông tin về

H

1y



thành phần VTG

* . Bởi vậy mà có thể giả thiết hệ số K41 bằng 0. Lập luận

1x

tương tự như vậy có thể đi tới kết luận là các hệ số: K21, K23, K31, K32, K52, K63 cũng bằng 0. Từ quan niệm về tính chất tương đồng của các hệ số khuếch đại, có thể cho rằng:

K11  K22

 K33  KH ,

còn

K42

 K43  K51  K53  K61  K62

 K.

Như vậy, số lượng những hệ số chưa biết của thuật toán lọc giảm từ 18 xuống còn 2.

Liên quan tới việc cắt giảm số lượng các hệ số khuếch đại của thuật toán (3.7), ta có thể viết lại nó dưới dạng đơn giản sau:

FH1x

 KHYH1x (t)  H*

FH1y KHYH1y(t)  H*

1y

1x 

 KYH1y (t)  H





FH1z  KHYH1z (t)  H*

F1x

1z

1z

1y

*  KYH1z (t)  H*

(3.8)

1x

1x

F1y  KYH1x (t)  H* F1z  KYH1x (t)  H*

 KYH1z (t)  H*

1z

1y

 KYH1y (t)  H*

3.2.2 Mô phỏng thuật toán lọc trên máy tính

3.2.2.1 Tổ chức chương trình

Chương trình sử dụng để khảo sát các thuật toán xác định định hướng của TBB bằng cách tạo giả (mô hình hóa) môi trường ngoài và tổng hợp các thuật toán xác định các thành phần VTG của TBB (chương 2) và mục 3.2.1. Cấu trúc chương trình có tính trước tới việc khảo sát những thuật toán phức tạp khi xác định định hướng không gian của TBB như đã giới thiệu ở chương 2.

Để thực tế hóa tính năng của bộ lọc, chương trình được viết trên ngôn ngữ MatLab [3]. Giao diện của chương trình hoàn toàn mở đối với người sử dụng, cho phép cập nhật, bổ sung, thay đổi và dễ dàng lập những mô hình thử nghiệm đa dạng. Tính mở của chương trình cho phép lặp lại tất cả những thí nghiệm mô hình đã được dẫn ra trong mục 3.2.1.

Chương trình mô phỏng tập hợp từ 2 modul chính: modul tính toán và modul giao diện.

3.2.2.2 Tổ chức khảo sát

Chương trình khảo sát cho phép thực hiện các thử nghiệm đa dạng. Trong phạm vi của luận án ta tập trung vào những thí nghiệm cơ bản, chứng minh mức độ tin cậy của những kết quả lý thuyết và khả năng ứng dụng thực tế.

Dữ liệu đầu vào chung cho tất cả các thử nghiệm là:

- độ nghiêng của VTT bằng -60o;

- vị trí góc ban đầu hệ TĐLK =0, =0, =0;

- tốc độ góc ban đầu các trục 1X

1Y

1Z

 5o / s ;

- các hệ số

KH  1,

K 1, T1x  T1y  T1z  1s .

Mục đích khảo sát nhằm rút ra những kết luận sau:

+ Khẳng định bằng thực nghiệm mô phỏng tính hội tụ (hoặc phân kỳ) thuật toán lọc phi tuyến đã tổng hợp được ở mục 3.3.1.

+ Khảo sát những tính chất động của thuật toán lọc (khảo sát quá trình quá độ của bộ lọc bằng thực nghiệm).

+ Khảo sát động học thống kê bộ lọc (xác định bằng thực nghiệm các sai số động học và nhiễu tạp).

3.2.2.3 Kết quả khảo sát.

a) Kết luận về tính hội tụ và phân kỳ của thuật toán.

Tính hội tụ của thuật toán tính trực tiếp các thành phần vector VTG của TBB theo các phép đo từ trường đã xét ở chương 2 chỉ có được khi có ít nhất một thông tin VTG độc lập bổ sung. Như vậy tính hội tụ của thuật toán tính thẳng các thành phần của vector VTG đã được giải quyết.

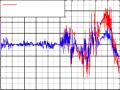
Vấn đề hội tụ của thuật toán lọc phi tuyến theo cấu trúc hình 3.1 sẽ phức tạp hơn. Với mô hình là phi tuyến, nên phương pháp phân tích tính ổn định dựa trên những khảo sát hệ số truyền hệ hở [6, 7] không áp dụng được. Ta chứng minh trong mô hình thực nghiệm rằng thuật toán lọc phi tuyến tĩnh (hệ số không đổi) đã được tổng hợp ở mục 3.3.1 là phân kỳ. Kết quả khảo sát thực nghiệm mô hình trên được dẫn ra ở hình 3.2.

H

* 1x

yH1x

K11 K51 K61

K22

FH1x

63



FH1y



FH1z



1 1x

H

*

p

H

*

1 1y

p -x

 x

1

H

p*

x

1z

* 1x



H

- x

H

x *

1y

H

* 1z

- x

yH1y

H

* 1y

yH1z

K42 K62

K33

K43 K53

H

* 1z

F1x



F1y



F1z







1

* 1x

p

1



T1x CB



1

* 1x

1y

p

1



T1y CB



1

* 1y

1z

p

1



Tz CB

1z

1x

63

1y

1z

Hình 3.1 Sơ đồ cấu trúc thuật toán lọc phi tuyến cận tối ưu VTG của TBB theo vector từ trường Trái đất