Phương Án Sử Dụng Duy Nhất Một Cảm Biến Vtg Độc Lập Là Con Quay Thẳng Đứng

Để đơn giản hóa các tính toán mà không làm mất đi tính chất chung, có

thể giả sử thành phần

Hz  0 . Điều đó có nghĩa là trục X của hệ tọa độ Trái

đất ban đầu cũng nằm trong mặt phẳng thẳng đứng chứa vector từ trườngH. Khi đó, vector từ trường H1 mà TBB đo được có dạng sau:

cos.cos.Hx  sin .H y

H1  (sin .sin  cos.sin .cos).Hx  cos.cos.H y

(sin .cos cos.sin .sin ).Hx  cos.sin .Hy

Ma trận Jacobi của vector H1

(2.5)

H (, , ) 1 	Hy1		Hy1		Hy1	 
(, , ) 						
 	Hz1		Hz1		Hz1	 
						

Có thể bạn quan tâm!

• Ý Nghĩa Của Việc Ổn Định Định Hướng Không Gian Cho Tbb Trinh Sát
• Những Khái Niệm Cơ Bản Về Từ Trường Trái Đất Và Cảm Biến
• Bản Chất Và Đặc Tính Của Sai Số Khi Đo Từ Trường Trên Thiết Bị Bay
• Phương Sai Sai Số Tổng Khi Xác Định Các Thành Phần Của Vtg
• Thuật Toán Lọc Phi Tuyến Các Thành Phần Vector Vtg Của Tbb
• Các Thuật Toán Lọc Phi Tuyến Khác Trong Tổng Hợp Bộ Đo Vtg Của Tbb

Xem toàn bộ 151 trang tài liệu này.

Hx1 Hx1

Hx1 





=

-cos.sin.Hx + +cos.Hy	-cos.sin.Hx	0
-cos.cos.cos.Hx- -sin.cos.Hy	(cos.sin + +sin.sin.cos).Hx	(sin.cos + +cos.sin.sin).Hx - -cos.sin.Hy
cos.cos.sin.Hx- -sin.sin.Hy	(cos.cos - -sin.sin.sin).Hx	(-sin.sin + +cos.sin.cos).Hx- -cos.cos.Hy

=

Để tính Jacobi (định thức

DetH1 (,, ) / (,, )), ta biến đổi sang

ma trận tương đương (giá trị định thức không bị thay đổi). Ta nhân hàng thứ 2 của định thức với sin, hàng thứ ba với cos và cộng chúng với nhau. Thay hàng tổng vào hàng thứ hai của định thức. Sau đó làm ngược lại, hàng thứ hai

của định thức ta nhân với cos, hàng thứ ba với sin và thực hiện trừ đi cho nhau. Kết quả ta đặt vào hàng thứ ba của định thức:

DetH1 (,, ) / (,, )

)



(cos.sin .Hx ) ( cos.sin .Hx  cos.Hy ) 0 





x

 (cos.H )

0 (cos.sin .Hx

 cos.Hy 

(sin .sin .Hx)

( cos cos.Hx  sin .Hy )

(sin .Hx ) 

Bổ sung thêm vào hàng thứ ba (sau khi đã nhân với cos) hàng đầu tiên đã được nhân với sin

DetH1 (,, ) / (,, )

)



( cos.sin .Hx ) ( cos.sin .Hx  cos.Hy ) 0 





x

 (cos.H )

0 (cos.sin .Hx

 cos.Hy 

 0

( cos.Hx )

(cos.sin .Hx ) 

Khai triển định thức theo hàng đầu tiên, ta có:

DetH1 (,, ) / (,, )

 cos.sin .Hx .

0

 cos.Hx

cos.sin .Hx  cos.Hy 

cos.sin .Hx

 (cos.Hy

 cos.sin .Hx

cos.H

)x

0

cos.sin .Hx  cos.Hy  0

cos.sin .H

Định thức bằng 0 của Jacobi

DetH1 (,, ) / (,, )

x

nói lên rằng,

không tồn tại hàm ngược (2.2). Tức là, khi tìm hiểu sự thay đổi của VTT H1,

ta không thể xác định vetor các góc Y1

định vị bộ đo

đơn trị.

(,, )T

một cách

Trục mà khi quay quanh 0 X1

Kết quả nhận được có giá trị rất lớn về mặt phương pháp. Nó cho phép ta không lãng phí thời gian đi tìm thuật toán đo định vị thân TBB khi chỉ dựa trên các phép đo từ trường, mà đi thẳng tới việc tổng hợp

nó, bộ đo vector không cảm biến được

H

Z1

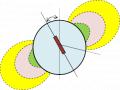
Hình 2.9 Giải thích không có khả năng định vị chỉ bằng các phép đo từ trường

thuật toán sử dụng thông tin bổ sung của những cảm biến khác.

Kết quả nhận được có cách mô tả hình học rất đơn giản và được thể hiện trên hình 2.9. Sự quay của bộ đo VTT quanh trục, mà trục này trùng với VTT, sẽ không làm thay đổi độ lớn các hình chiếu của VTT trên các phần tử của bộ đo. Chính vì vậy ta sẽ có vô số cách định vị bộ đo, khi các hình chiếu của VTT lên các phần tử của bộ đo không thay đổi.

2.4.2 Mô hình đo VTT Trái đất kết hợp với nguồn thông tin độc lập khác để ĐKĐH cho TBB

1. Đặt vấn đề.

Y1



O

Z1



tt

X1

p

H1

Nếu như ta coi vector từ trường

(VTT) Trái đất

H1 trong một không gian

hữu hạn nào đó là xác định và bất biến, thì hoàn toàn có thể lấy nó làm gốc để xét sự quay của TBB. Sự quay của TBB tương đối so với VTT, để thuận tiện trong việc phân tích và xây dựng mô hình toán học, cũng có thể coi là VTT quay trong hệ tọa

Hình 2.10 Sự quay của VTT trong hệ TĐLK

độ liên kết (TĐLK) của TBB với vector VTG là ω (hình 2.10). Dấu “-” ở

đây đặc trưng cho sự ngược pha giữa hai hệ quy chiếu đã nêu. Dựa trên giả thiết đó, ta cần phải xác định: mô hình toán học; những đặc điểm và sai số các phép đo VTG của VTT và TBB. Để chứng minh tính đúng đắn của mô hình đã xây dựng, ta tiến hành khảo sát nó nhờ mô phỏng trên máy tính.

2. Mô hình toán học phép đo VTT trong hệ TĐLK

a. Phương pháp xác định vận tốc góc của vector từ trường

Vector ω

cần đo đặc trưng cho sự quay của VTT

H1 được tách thành

hai vector thành phần: vector tiếp tuyến

ωtt

hướng dọc theo

H1 ; vector

pháp tuyến

ωp

vuông góc với

H1 . Vector tiếp tuyến không làm thay đổi

VTT cần đo trong hệ TĐLK.

Theo định nghĩa về VTG [35,40], khi coi vector H1 là vector bán kính, ta có thể viết:

dH1 / dt ω H1 

(2.6)

trong đó vế phải là phép tính nhân vector. Phép nhân vector dưới dạng tọa độ của hệ liên kết trên TBB có thể biểu diễn bằng một định thức:

dH1 dt

i

ω1x

j

ω1y

k

ω1z

(2.7)

H1x

H1y

H1z

Trong đó: i, j, k là các vector đơn vị định hướng tương ứng theo các trục X1, Y1, Z1 của hệ TĐLK.

Khai triển định thức (2.7) theo dòng đầu tiên có thể nhận được hệ các

phương trình đại số tuyến tính đối với các thành phần của vector :

 dH1x

 .H

 .H

 dt

1y 1z

1z 1y

dH1y

 .H

 .H

 dt

1x 1z

1z 1x

(2.8)

dH



1z1x .H1y 1y .H1x

 dt

Định thức chính của hệ (2.8) có dạng sau và bằng 0 theo chứng minh ở mục 2.4.1:

Det(2.8) 

0

H1z

 H1y

 H1z 0

H1x

H1y

 H1x  0 0

Có nghĩa rằng thành phần tiếp tuyến

tt

của vector VTG không có ảnh

hưởng tới đạo hàm của VTT cần đo ( dH1 / dt ) như đã nêu và phép đo vector

dH1 / dt

theo (2.8) có kết quả đa trị.

b. Khắc phục tính đa trị bằng cách bổ sung thông tin vận tốc góc từ các phép đo độc lập

Do hệ phương trình (2.8) không thể giải một cách đơn trị đối với các thành phần vector VTG đo bằng từ trường, nên cần phải bổ sung cho hệ này những thông tin đo VTG độc lập từ loại cảm biến khác. Ta phân tích và lựa chọn nguồn thông tin cần bổ sung như sau:

+ Bổ sung thông tin theo thành phần 1x

Giả sử ta đưa thêm vào thành phần các phép đo (2.8) giá trị đo độc lập của cảm biến VTG 1x, ký hiệu là W. Hệ phương trình (2.8) khi đó sẽ có dạng mới:

dH1x

 .H

 .H

 dt

dH1y

1y

 W.H

1z 1z 1y

 .H

(2.9)

 dt

1z 1z 1x

dH



1zW.H

 .H

 dt

1y 1y 1x

Bỏ đi phương trình đầu tiên trong hệ (2.9), ta nhận được biểu thức trực tiếp đối với các thành phần vận tốc góc 1y và 1z của TBB mà chưa đo được:

 (W.H dH1y ) / H

1z



1z dt 1x

dH

(2.10)

1y  (W.H1y 1z ) / H1x

 dt

Hệ phương trình (2.10) cho phép ta nhận được tất cả các thành phần VTG còn lại của TBB theo các giá trị đo W của một cảm biến VTG độc lập và bộ đo VTT ba trục. Kết luận trên có ý nghĩa thực tế rất lớn bởi vì nó cho phép xây dựng một bộ cảm biến VTG 3 trục trên cơ sở của một cảm biến từ trường 3 trục và một cảm biến VTG đều dùng công nghệ MEMS [13, 25].

Từ hệ phương trình (2.10) ta thấy là nó chỉ giải được khi

+ Bổ sung thông tin theo thành phần 1y

H1x  0 .

Tương tự như trên, nhờ phép đo độc lập mà ta biết được thành phần VTG 1y. Ký hiệu thành phần này là V, khi đó hệ phương trình (2.8) sẽ có dạng:

 dH1x

 dt

V.H1z 1z .H1y

dH1y

 .H  .H

(2.11)

 dt

 dH1z

1x 1z 1z 1x



 dt

1x .H1y  V.H1x

Bỏ đi phương trình thứ 2 ở hệ trên, ta nhận được biểu thức trực tiếp cho các thành phần chưa biết của vector vận tốc góc:

1z  (V.H1z dH1x ) / H1y







1x  (V.H 1x 

dt dH1z

dt

) / H1y

(2.12)

Từ hệ phương trình (2.12) ta thấy nó giải được chỉ khi

+ Bổ sung thông tin theo thành phần 1z

H1y  0.

Giả sử do phép đo độc lập ta biết được thành phần VTG 1z. Ký hiệu thành phần đo được là R, khi đó hệ phương trình (2.8) sẽ có dạng:

 dH1x

 dt

1y .H1z  R.H1y

dH1y

 dt

1x .H1z  R.H1x

(2.13)



dH1z

1x .H1y 1y .H1x

 dt

Bỏ đi phương trình thứ 3 của hệ trên, ta nhận được biểu thức trực tiếp cho các thành phần chưa biết của vector vận tốc góc:

1y  (R.H1y dH1x ) / H1z







1x  (R.H1x 

dt dH1y

dt

) / H1z

(2.14)

Từ hệ phương trình (2.14) suy ra là nó giải được chỉ khi có

H1z

 0 .

3. Phương án sử dụng duy nhất một cảm biến VTG độc lập là con quay thẳng đứng

Xét các hệ phương trình (2.10), (2.12) và (2.14) ta thấy rằng các hệ này không giải được khi mẫu số của chúng bằng 0, tức là khi các thành phần (H1x, H1y, H1z) của VTT bằng 0. Nếu sử dụng 2 cảm biến VTG độc lập, đặt vuông góc với nhau, thì với định hướng bất kỳ của TBB, ta có khả năng chọn một cặp phương trình để xác định thành phần thứ 3 còn lại của vetor VTG. Tuy nhiên, theo tư duy kinh tế và đơn giản về kỹ thuật, ta chỉ sử dụng duy nhất một cảm biến VTG độc lập để làm nguồn thông tin bổ sung. Ý tưởng đó dẫn tới việc phải chọn vị trí đặt trục nhạy của cảm biến VTG theo một trong 3 trục (X1, Y1, Z1) của hệ TĐLK.

Lựa chọn: Đối với vùng giữa (gần xích đạo) [40] của Trái đất, nơi mà

VTT có thành phần thẳng đứng lớn hơn hẳn các thành phần ngang, tốt nhất nên đặt trục nhạy của cảm biến VTG dọc theo trục OY1 của hệ TĐLK trên TBB. Khả năng thành phần H1y=0 chỉ có thể có khi góc liệng của TBB bằng góc nghiêng của VTT (mà góc nghiêng của VTT là 60o hoặc lớn hơn). Như

vậy TBB sẽ không bao giờ có thể có góc liệng lớn như vậy do hạn chế về quá tải vật bay, góc liệng của TBB không vượt quá 30o.

2.4.3 Phân tích sai số đo các thành phần vận tốc góc của TBB thông qua đo từ trườngg trái đất

1. Nguồn gốc các sai số

Hệ phương trình (2.12), khi đặt cảm biến VTG dọc theo trục đứng OY1 hệ TĐLK của TBB có dạng:

1z  (V.H1z dH1x ) / H1y







1x  (V.H 1x 

dt dH1z

dt

) / H1y

Ở đây V là giá trị đo VTG quay TBB quanh trục OY1 của cảm biến độc lập.

Sai số tính các thành phần vector vận tốc góc 1z và 1x xuất hiện do các sai số của dữ liệu đầu vào: V, H1x, H1y, H1z, kể cả sai số tính đạo hàm (trong

trường hợp ta đang xét chính là các sai số tính

dH1x / dt

và dH1z / dt ). Mặt

khác, các sai số tính đạo hàm lại phụ thuộc vào sai số đo các thành phần H1x và H1z. Ta viết các phương trình (2.12) dưới dạng tổng quát:

1z  F(V,dH1x / dt, H1y , H1z )

 G(V,dH

/ dt, H , H )

(2.15)

1x

1z 1x 1y

1z

Sai số phép đo các thành phần VTG có thể biểu diễn dưới dạng các phương trình vi phân đầy đủ của các hàm F và G:

1y

1x

1z  Fv .V  FdH / dt .(dH1x / dt)  FH

.H1y  FH .H1z

(2.16)

1z

1x  Gv .V  GdH

/ dt .(dH1z / dt)  GH .H1x  GH

.H1y

1x

1y

trong đó các chỉ số dưới các hàm F và G có nghĩa là các đạo hàm riêng, ví dụ Fv F/ V . Ta sẽ gọi các đạo hàm riêng là các hệ số ảnh hưởng của phép

đo sơ cấp tới sai số kết quả đo.

Trong bảng 2.3 dưới đây sẽ dẫn ra tất cả các sai số và hệ số có ảnh hưởng tới kết quả đo

Bảng 2.3 Sai số trung bình bình phương tương đối của tạp

Phép đo sơ cấp

Biểu thức của hệ số ảnh hưởng Fkhi tính 1z	Biểu thức của hệ số ảnh hưởng Gkhi tính 1x
V - vận tốc góc quanh trục OY1	Fv=H1z/H1y	Gv=H1x/H1y
H1x - thành phần VTT dọc theo trục OX1	FdH1x/dt=1/H1y	GH1x=V/H1y
H1y - thành phần VTT dọc theo trục OY1	FH1y=-1z/H1y	GH1y=-1x/H1y
H1z - thành phần VTT dọc theo trục OZ1	FH1z=V/H1y	GdH1z/dt=-1/H1y

2. Phân tích ảnh hưởng và ý nghĩa hình học của các sai số sơ cấp

Từ bảng 2.3 ta thấy tất cả các hệ số ảnh hưởng đều chứa một thừa số