Các Thuật Toán Lọc Phi Tuyến Khác Trong Tổng Hợp Bộ Đo Vtg Của Tbb

yH(t)

H*(t)

F(t)

*(t)

a) Đầu vào

yH1x và đầu ra (đánh

b. Đầu vào F1x

và đầu ra 1X

Có thể bạn quan tâm!

• Phương Án Sử Dụng Duy Nhất Một Cảm Biến Vtg Độc Lập Là Con Quay Thẳng Đứng
• Phương Sai Sai Số Tổng Khi Xác Định Các Thành Phần Của Vtg
• Thuật Toán Lọc Phi Tuyến Các Thành Phần Vector Vtg Của Tbb
• Mô Phỏng Đánh Giá Các Mô Hình Hệ Thống Xác Định Vtg Đã Xây Dựng
• Nghiên cứu xác định định hướng không gian của thiết bị bay theo các phép đo từ trường trái đất - 13
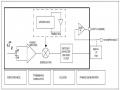
• Thiết Kế Và Tổ Chức Phần Cứng Thực Nghiệm

Xem toàn bộ 151 trang tài liệu này.

H

1X

giá) *

bộ lọc theo trục X1.

bộ lọc theo trục X1.

yH(t)

H*(t)

F(t)

*(t)

c. Đầu vào

yH1y

và đầu ra (đánh

d. Đầu vào

F1y

và đầu ra 1y

H

1y

giá) *

bộ lọc theo trục Y1.

bộ lọc theo trục Y1.

yH(t)

H*(t)

F(t)

*(t)

e. Đầu vào

yH1z

và đầu ra (đánh

f. Đầu vào F1z và đầu ra 1z bộ

H

1z

giá) *

bộ lọc theo trục Z1.

lọc theo trục Z1.

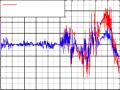
Hình 3.2 Kết quả mô phỏng mô hình lọc phi tuyến hệ số tĩnh.

Rõ ràng là khi VTG quay của TBB không đổi sẽ xảy ra mất bám, tức là thuật toán không hội tụ. Việc chứng minh tính hội tụ không thể căn cứ trên những ví dụ thử nghiệm, nhưng để chứng minh tính chất phân kỳ của thuật toán thì chỉ cần một kết quả thử nghiệm nêu trên đã khẳng định tính phân kỳ của thuật toán lọc phi tuyến với hệ số không đổi.

Nghiên cứu nguyên nhân phân kỳ của thuật toán lọc phi tuyến tĩnh cho ta rút ra kết luận rằng phương pháp tính tín hiệu sai số để lọc các thành phần VTG (3.8) không tính tới bản chất vector của VTG. Khi quay bộ đo tới một

góc 180o, dấu của tín hiệu sai số

F1x

thay đổi và xảy ra mất bám. Cũng phân

tích tương tự đối với các phương trình lọc phi tuyến động (hệ số thay đổi) cho thấy rằng, khi lọc động sự mất bám không xảy ra, bởi vì đồng thời với sự thay đổi dấu của tín hiệu sai số thì dấu của hệ số truyền (tản mát tương quan của sai số đánh giá các vector thành phần từ trường và VTG của TBB) cũng thay đổi.

Với thực trạng như vậy ta cần xuất cải tiến thuật toán lọc phi tuyến đã tổng hợp. Sự cải tiến liên quan tới phương pháp tính (3.8) cho các tín hiệu sai số

F1x ,

F1y ,

F1z . Biểu thức tính các sai số bám sát khi cải tiến có dạng sau:

FH1x

FH1y F

 KH

 KH

 K

H

H1x H1y

Y



Y



Y

(t)  H* 

1x

1y

(t)  H* 



(t)  H* 

H1z

H1z 1z

Y

* *

(3.8)*

F1x

 KYH1y (t).H1z  YH1z (t).H1y

F1y F1z

 K

 K

Y

H1z H1x

(t).H*

1x

1y

(t).H*

 YH1x

 YH1y

(t).H* 

1z

1x

(t).H* 

Các thay đổi chỉ liên quan tới các phương trình tính tín hiệu sai số

F1x ,

F1y ,

F1z . Phương pháp tính các tín hiệu đã đề xuất ở trên, không khác gì

phương pháp nhân vector của hỗn hợp đầu vào

y , y ,

H

H

1x 1y

yHz

với những

vector đánh giá tương ứng (với dấu ngược lại). Như vậy, tín hiệu sai số tỷ lệ

H

với sin của góc quay vector đánh giá

* (trong trường hợp góc nhỏ thì tỷ lệ

1

với chính góc đó) so với vector đầu vào hỗn hợp y(t) trong mặt phẳng quay đối với các thành phần VTG cần phải đánh giá. Trong phương pháp (3.8)* giá trị tín hiệu sai số tỷ lệ với giá trị tín hiệu sai số theo phương pháp (3.8), nhưng trong tín hiệu sai số (3.8)* lại chứa thông tin về dấu góc quay.

Ta gọi thuật toán tính tín hiệu sai số (3.8)* là thuật toán lọc phi tuyến với tín hiệu sai số tiên nghiệm. Dưới đây là kết quả thử nghiệm thuật toán này, phản ánh tính chất hội tụ của thuật toán (xem hình 3.3).

F(t)

*(t)

yH(t)

H*(t)

a. Đầu vào

yH1x

và đầu ra (đánh

b. Đầu vào F1x

và đầu ra 1x bộ

H

1x

giá)

* bộ lọc theo trục X1

lọc theo trục X1.

yH(t)

H*(t)

F(t)

*(t)

.

c. Đầu vào

yH1y và đầu ra (đánh

d. Đầu vào F1y và đầu ra

1y bộ

H

1y

giá) *

bộ lọc theo trục Y1.

lọc theo trục Y1

yH(t)

H*(t)

F(t)

*(t)



e. Đầu vào

yH1z và đầu ra (đánh giá)

f. Đầu vào

F và đầu ra (đánh giá)



1Z

1Z

H

1z

* bộ lọc theo trục Z1.

* bộ lọc theo trục Z1.

F(t)

*(t)

g. Sai số đo VTG

1x

khi giá trị trung

h. Sai số đo VTG

1z

khi giá trị trung

bình bình phương nhiễu tạp là 5dB. bình bình phương nhiễu tạp tăng.

Hình 3.3 Kết quả mô phỏng thuật toán lọc phi tuyến hệ số động

b) Kết luận về các tính chất động học của thuật toán.

Khảo sát các tính chất động học đối với thuật toán lọc phi tuyến với tín hiệu sai số tiên nghiệm cho phép ta rút ra những kết luận sau:

+ Thuật toán lọc phi tuyến với tín hiệu sai số tiên nghiệm có động học được phản ánh trên những đồ thị hàm đánh giá các thành phần VTG (hình 3.3b và 3.3f) cho ta thấy rõ, sai số tĩnh đặc trưng bởi tính ổn định của VTG theo các trục X1 và Z1. Ngoài sai số tĩnh, thuật toán lọc phi tuyến động có thời gian quá độ là 2 giây với các hệ số truyền trong mô hình khảo sát. Trên các đồ thị còn thấy rõ cả những vùng tăng bất thường sai số bám sát, gần với vùng phân kỳ của thuật toán lọc tĩnh (hình 3.2b và 3.2f).

c) Kết luận về ảnh hưởng của sai số tạp âm tới thuật toán

Trong thử nghiệm mô phỏng đối với thuật toán lọc phi tuyến động khi có những tác động của tạp âm dưới dạng sai số trung bình bình phương bằng 5dB (hình 3.3b và 3.3f) ta thấy rằng, khi có nhiễu tạp đồ thị đánh giá sai số đo VTG cho thấy có cả những vùng sai số không mong đợi. Bản chất những vùng đó đã được phân tích trong phần đánh giá sai số tính đạo hàm ở chương 2.

3.3 Các thuật toán lọc phi tuyến khác trong tổng hợp bộ đo VTG của TBB

Với mục đích lựa chọn thêm những thuật toán lọc phi tuyến, đáp ứng yêu cầu xác định chính xác VTG của TBBKNL theo thông tin từ trường kể cả những trường hợp có ảnh hưởng của nhiễu tạp, ta có thể áp dụng những thuật toán hiện đại sau [1, 12, 43].

3.4.1. Sử dụng thuật toán lọc Kalman rời rạc mở rộng (Extended Kalman filter - EKF)

Thuật toán lọc Kalman rời rạc mở rộng được sử dụng để ước lượng các trạng thái cũng như các tham số của hệ thống bất định có mô hình động học phi tuyến hoặc mô hình đo phi tuyến. Ta xét hệ thống rời rạc được biểu diễn trong không gian trạng thái như sau:

+ Phương trình mô tả động học của hệ thống:

xk  fk1 (xk1, tk1 )  wk1

+ Phương trình phép đo:

zk  hk (xk )  vk

(3.9)

(3.10)

Ở đây f và h là các hàm vector phi tuyến, còn wk và vk là các nhiễu quá trình và tạp đo tương ứng. Chúng được giả thiết là tạp trắng Gauss với kỳ vọng toán học bằng 0 và mật độ phổ đã biết. Các phương trình thuật toán lọc Kalman mở rộng có dạng [34, 43]:

xˆ 0 Ex0

+ Khởi tạo bộ lọc: P

 E(x

 xˆ )(x  xˆ

)T 

(3.11)

T

X0

0 0 0 0

Ở đây:

Ex

 E H H H



0 1x0 1y0 1z0 1x0 1y0 1z0

E(H  Hˆ )20 0 0 0 0

1x 0 1x 0 

0 E(H  Hˆ )20 0 0 0



2

1y0 1y0

- PX

0 0 E(H1z0  Hˆ1z0 ) 0 0 0 

(3.11)*

00 0 0 E(ˆ )20 0 

1x 0 1x 0 

0 0 0 0 E(ˆ )20 

1y0 1y0 

0 0 0 0 0 E(ˆ )2

1z0 1z0 

+ Phương trình ước lượng trạng thái dự báo:

xˆ k()  fk1xˆ k1()

+ Phương trình tính phép đo dự báo:

zˆk hkxˆ k()

+ Phương trình hiệu chỉnh dự báo theo phép đo:

(3.12)

(3.13)

xˆ k

()  xˆ

k ()  Hk

(zk

 zˆk),

Hk 

hk

x

x xˆ k

()

(3.14)

+ Phương trình tính ma trận phương sai tiên nghiệm:

Pk ()  AkPk

() AT  Q

k1 ,

Ak 

dfk

dx

x x

k

k 1

()

(3.15)

+ Phương trình tính hệ số khuếch đại lọc:

K ()  P () HTHkPk ()HTRk1

(3.16)

k k k k

+ Phương trình tính ma trận phương sai hậu nghiệm:

Pk () I  Kk Hk Pk ()

(3.17)

Để áp dụng thuật toán lọc Kalman rời rạc mở rộng cho bài toán ước lượng mà chúng ta đang nghiên cứu. Ta sẽ cụ thể hoá các hàm của mô hình quá trình, mô hình đo; các tham số về nhiễu quá trình, nhiễu đo; các tham số về hằng số thời gian của quá trình Markov.

Vector trạng thái cần được ước lượng được thể hiện ở (3.2). Hệ phương trình vi phân ngẫu nhiên mô tả quá trình được thể hiện ở (3.3) và (3.4). Mô hình quan sát ở đây đơn giản chỉ là 4 phép đo H1x, H1y, H1z và 1y .

Để áp dụng thuật toán lọc rời rạc ta cần rời rạc hoá các phương trình vi phân liên tục (3.3) và (3.4). Ta không thể trực tiếp áp dụng các phương pháp số thông thường do đặc điểm không khả vi của tạp trắng. Do vậy trước tiên cần xấp xỉ hóa tạp trăng bởi mô hình trước giới hạn, sau đó mới áp dụng các phương pháp số. Mô hình trước giới hạn của quá trình là một chuỗi các xung vuông không tương quan với độ rộng Δt và có biên độ ngẫu nhiên phân bố Gauss. Mật độ phổ của chuỗi xung này ở vùng thấp tần sẽ trùng với mật độ phổ của tạp trắng Hệ phương trình (3.3) được rời rạc hóa bằng phương pháp gần đúng tích phân Euler, còn hệ phương trình (3.4) được rời rạc hoá bằng phương pháp chuyển đổi tổng quát. Từ đó ta nhận được hệ phương trình sau:

H (k 1)  H (k)  T* (k)H (k)  (k)H (k)

1x 1x 1y 1z 1z 1y

H (k 1)  H (k)  T*  (k)H (k)  (k)H (k)

1y 1y 1x 1z 1z 1x

H (k 1)  H (k)  T* (k)H (k)  (k)H (k)

1z 1z 1x 1y 1y 1x

 (k 1)  (1 T ) (k)  w (k)

1x



T1x

1x x

 (k 1)  (1 

T )

(k)  w (k)

1y



T1y

1y y

 (k 1)  (1 

T )

(k)  w (k)

1z



T1z

1z z

Các phương trình mô tả kênh quan sát khi đã rời rạc hóa là:

z1 (k)  H1x (k)  vHx (k)

z (k)  H (k)  v (k)

2 1y Hy

z (k)  H (k)  v (k)

3 1z Hz

z4(k) 1y (k)  vy (k)

Các tham số được lựa chọn khi tiến hành mô phỏng thuật toán lọc Kalman rời rạc mở rộng:

- Vector trạng thái ban đầu:

x(0) 0.5(Gauss)  0.9(Gauss) 0.0(Gauss) 0.0(rad / s) 0.0(rad / s) 0.0(rad / s)T

- Ma trận phương sai ban đầu:

2.0e  3(Gauss2 ) 0.0 0.0 0.0 0.0 0.0 



0.0 2.0e  3(Gauss2 ) 0.0 0.0 0.0 0.0 

0.0 0.0 2.0e  3(Gauss2 ) 0.0 0.0 0.0 

P(0) 

0.0 0.0 0.0 2.0(rad / s)2 0.0 0.0 



0.0 0.0 0.0 0.0 2.0(rad / s)2 0.0 

0.0 0.0 0.0 0.0 0.0 2.0(rad / s)2 



- Mật độ phổ công suất của nhiễu quá trình:

Q  diag 0.0, 0.0, 0.0, 7.0e  6(1/ s3 ), 7.0e  6(1/ s3 ), 7.0e  6(1/ s3 )

- Mật độ phổ công suất nhiễu đo:

R  diag 3.136e  8(Gauss2 / s), 3.136e  8(Gauss2 / s), 3.136e  8(Gauss2 / s), 1.0e 10(1/ s) 

- Các hằng số thời gian của quá trình Markov:

T1x  T1y  T1z  0.10(s)

- Ma trận phương sai sai số tiên nghiệm:

H  Hˆ ()H  Hˆ ()T

1x,k 1x,k 1x,k 1x,k 

H  Hˆ ()H  Hˆ ()

1y,k 1y,k 1y,k 1y,k 

H  Hˆ () H  Hˆ () 





Pk ()  E 

1z,k 1z,k

1z,k 1z,k

1x,k ˆ1x,k () 1x,k ˆ1x,k () 

ˆ () ˆ () 

1y,k 1y,k 1y,k 1y,k 

ˆ () ˆ () 

1z,k 1z,k 1z,k 1z,k 

- Ma trận phương sai sai số hậu nghiệm:

H  Hˆ ()H  Hˆ ()T

1x,k 1x,k 1x,k 1x,k 

H  Hˆ ()H  Hˆ ()

1y,k 1y,k 1y,k 1y,k 

H  Hˆ () H  Hˆ () 





Pk ()  E 

1z,k 1z,k

1z,k 1z,k

1x,k ˆ1x,k () 1x,k ˆ1x,k () 

ˆ () ˆ () 

1y,k 1y,k 1y,k 1y,k 

ˆ () ˆ () 

1z,k 1z,k 1z,k 1z,k 

Từ đó ta có thể cụ thể hóa các phương trình của thuật toán lọc Kalman rời rạc mở rộng như sau:

- Phương trình cập nhật thời gian:

*

1x,k 1x,k 1 

H ()  H ()  T  ()H ()  ()H ()

1y,k 1 1z,k 1 1z,k 1 1y,k 1

H ()  H ()  T*  ()H ()  ()H ()

1y,k 1y,k 1

1x,k 1 1z,k 1 1z,k 1 1x,k 1 

*

1z,k 1z,k 1 

H ()  H ()  T  ()H ()  ()H ()

1z,k 1 1y,k 1 1y,k 1 1x,k 1

 ()  (1T ) ()

1x,k



T1x

1x,k 1

 ()  (1

T )

()

1y,k



T1y

1y,k 1

 ()  (1 T )

()

1z,k



T1z

1z,k 1

- Phương trình dự báo phép đo: