Ngưỡng Các Giá Trị Phân Loại Tình Trạng Khô Hạn Theo Chỉ Số Spi

Tiến hành tiêu chuẩn hóa hàm xác suất lũy tích gamma, từ công thức (2-3) và (2-4) ta có được công thức xác định giá trị xác suất lũy tích như sau:

Fx x 1 eZ 2 2 dx 0 2

(2-5)

Có thể bạn quan tâm!

Đặc Điểm Địa Hình Lưu Vực Sông Phan – Cà Lồ‌
Diện Tích Sử Dụng Đất Của Vùng Nghiên Cứu Năm 2015‌
Lượng Mưa Năm Tại Các Trạm Vùng Nghiên Cứu‌
Kết Quả Tính Kappa Trạm Tam Đảo T12 Đến T5‌
Nghiên cứu ứng dụng các chỉ số đánh giá tình trạng khô hạn trong đánh giá nguồn nước và giám sát tình hình thiếu hụt nguồn nước vùng sông Phan - Cà Lồ - 9
Nghiên cứu ứng dụng các chỉ số đánh giá tình trạng khô hạn trong đánh giá nguồn nước và giám sát tình hình thiếu hụt nguồn nước vùng sông Phan - Cà Lồ - 10

Xem toàn bộ 82 trang tài liệu này.

Từ công thức (4) tính toán theo phương pháp gần đúng ta được:

c c c t 2 

Z SPI St  0 1 2 

 1d t d t 2 d t 3 

1 2 3

(2-6)

- Trong đó: t  ln1 F 2 ; S = 1 khi F > 0.5 ; S = -1 khi F ≤ 0.5; c0 = 2.515517; c1 =

0.802853; c2 = 0.010328; d1 = 1.432788; d2 = 0.189269; d3 = 0.001308 (c0, c1, c2, d1, d2, d3 là

các hằng số của hàm phân phối chuẩn).

- Theo Tổ chức Khí tượng thế giới WMO thì tình trạng khô hạn hay ẩm ướt được phân cấp theo chỉ số SPI như trong bảng 2.3. Các chỉ số SPI có thể được tính toán cho nhiều thời đoạn khác nhau, thường là trong phạm vi từ 1 tháng, 3 tháng, 6 tháng … đến 48 tháng. Các chỉ số SPI với thời đoạn 1 tháng thể hiện tính chất hạn hán theo từng tháng (được tính từ lượng mưa trung bình tháng), thời đoạn 3 tháng thể hiện tính chất hạn hán theo mùa, vụ 3 tháng (được tính từ lượng mưa trung bình trong 3 tháng liên tiếp), thời đoạn 6 tháng thể hiện tính chất hạn hán theo mùa, vụ 6 tháng (được tính từ lượng mưa trung bình trong 6 tháng liên tiếp)… Trong luận văn này học viên sẽ so sánh, đánh giá diễn biến hạn hán theo các chỉ số hạn với hiện trạng hạn hán trong sản xuất nông nghiệp, trong khi mùa vụ sản xuất nông nghiệp thường là 3 tháng hoặc 6 tháng. Do đó, luận văn này sẽ chỉ tính toán giá trị của các chỉ số SPI với quy mô thời gian là 1 tháng, 3 tháng và 6 tháng. Chỉ số SPI với thời đoạn tính toán là 1 tháng, 3 tháng và 6 tháng được ký hiệu lần lượt là SPI1, SPI3 và SPI6.

- Để đánh giá mức độ hạn hán ta phải so sánh các giá trị của SPI với các ngưỡng của bảng phân loại hạn hán:

Bảng 2.3 Ngưỡng các giá trị phân loại tình trạng khô hạn theo chỉ số SPI

Các giá trị của SPI

Phân loại hạn
SPI ≥ 2	Cực kỳ ẩm ướt
1.99 ≥ SPI ≥ 1.5	Rất ẩm ướt
1.49 ≥ SPI ≥ 1.0	Tương đối ẩm ướt
-0.99 ≤ SPI ≤ 1.0	Gần chuẩn
-1.0 ≤ SPI ≤ -1.49	Tương đối hạn
-1.99 ≤ SPI ≤ -1.5	Hạn nặng
SPI ≤ -2	Hạn cực nặng

Ưu điểm

- Sử dụng SPI để đánh giá hạn khí tượng sẽ không cần sử dụng nhiều thông số khác: bốc hơi, độ ẩm -> giảm khối lượng tính toán.

- Dễ dàng sử dụng để tính toán dự báo hạn khi mưa dự báo đã và đang phát triển cả về số lượng lẫn chất lượng.

Nhược điểm

- Do việc chỉ sử dụng giá trị lượng mưa nên không thể đánh giá hết được toàn diện vè tình hình hạn hán trên lưu vực.

- Cần có chuỗi số liệu trong thời gian dài, liên tục.

Ý nghĩa

- Đánh giá tình hình hạn hán dựa trên chỉ số chuẩn hóa lượng mưa SPI thể hiện sự chênh lệch của lượng lượng mưa thực tế (tổng lượng mưa tuần, tháng, mùa, vụ thực tế) so với trung bình nhiều năm và chia cho độ lệch chuẩn. Việc tính toán chỉ số SPI có thể giúp đánh giá hạn theo từng tháng hoặc từng giai đoạn mùa vụ tùy vào mục đích

tính toán trong từng trường hợp cụ thể.

- Từ việc đánh giá hạn ta có thể dự báo, đưa ra biện pháp ứng phó đối với vùng nghiên cứu nhằm mục đích nâng cao hiệu quả sản xuất công nghiệp, nông nghiệp và chất lượng cuộc sống.

Dựa trên công thức tính toán cơ bản đã nêu ở trên, chỉ số SPI được tính toán bằng phương pháp lập bảng (Microsoft Excel) hoặc bằng các phần mềm viết sẵn. Trong luận văn này, tác giả sử dụng phần mềm tính toán SPI được viết sẵn và cung cấp miễn phí bởi Trung tâm giảm thiểu hạn hán quốc gia Đại học Nebraska, Mỹ (https://drought.unl.edu).

2.3 Ứng dụng chỉ số cán cân nước trong đánh giá hạn‌

Chỉ số cán cân nước K được tính theo công thức sau:

Trong đó:

: Lượng bốc hơi Piche thời đoạn tính toán : Lượng mưa thời đoạn tính toán

Hạn hán xảy ra khi lượng bốc hơi bắt đầu vượt quá lượng mưa rơi xuống. Qua đó ta có các ngưỡng chỉ tiêu theo bảng sau:

Bảng 2.4. Ngưỡng các giá trị phân loại tình trạng khô hạn theo chỉ số K‌

Các giá trị của K

Phân loại
K < 0.5	Rất ẩm
0.5 ≤ K ≤ 1.0	Ẩm
1.0 ≤ K ≤ 2.0	Hơi khô
2.0 ≤ K ≤ 4.0	Khô
K > 4	Rất khô

 Ưu điểm

- Đánh giá tình hình hạn hán vùng nghiên cứu dựa trên nhiều yếu tố: lượng mưa, bốc hơi nên đánh giá mức độ hạn toàn diện hơn.

 Nhược điểm

- Thực tế thu thập số liệu khó khăn, không đầy đủ.

2.4 Phân tích lựa chọn công cụ GIS để phân tích tình trạng thiếu hụt nguồn nước

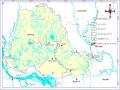
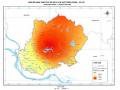
Sử dụng phần mềm Arcgis biên tập thể hiện các lớp nền cần thể hiện lên trên bản đồ. Số liệu tính toán SPI1,3,6,12 tại 10 vị trí dưới dạng định dạng excel sẽ đưa lên trên bản đồ dựa vào tọa độ địa lý của các trạm đo. Sử dụng phép nội suy nghịch đảo khoảng cách (Inverse Distance Weighting – IDW) được sử dụng để nội suy giá trị SPI của 10 trạm khí tượng thủy văn thuộc khu vực nghiên cứu để thể hiện bản đồ hạn của vùng.

Bản chất Phương pháp nội suy IDW là kỹ thuật nội suy tất định cục bộ, phương pháp này ước lượng các giá trị của một điểm bất kỳ bằng cách lấy trung bình các giá trị của các điểm lân cận của mỗi điểm tính trong đó mỗi điểm sẽ có một trọng số phụ thuộc vào khoảng cách của điểm đó với điểm cần ước lượng. Trong IDW người ta giả thiết rằng giá trị tại những điểm cần tính là trung bình trọng số - khoảng cách của các giá trị tại điểm mẫu trong khu vực lân cận của điểm cần tính (Chen & Liu,2012)[32]. Theo đó, IDW cho rằng những điểm gần với điểm dự báo hơn sẽ có ảnh hưởng hơn những điểm ở xa hơn điểm dự báo.

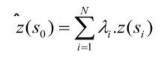(1)

là giá trị được dự báo tại điểm s0

N là số điểm mẫu trong khu vực lân cận của điểm s0

λi là các trọng số phụ thuộc vào khoảng cách từ mỗi điểm mẫu đến điểm s0 z(si) giá trị được đo đạc tại mỗi điểm mẫu i

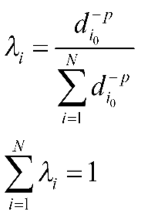
(2)

- di0 là khoảng cách giữa điểm dự báo s0 với điểm mẫu si

- p là tham số biểu hiện tốc độ giảm trọng số khi khoảng cách tăng. Trong nghiên cứu này sẽ chọn p = 2. (tức là chọn trọng số sẽ giảm theo bình phương khoảng cách).

Ưu điểm:

- IDW được đề xuất nên sử dụng khi có một tập hợp các điểm, phân bố rộng khắp bề mặt tính toán.

- Phương pháp này nhanh chóng, dễ thực hiện

Nhược điểm:

- Cần có số liệu của nhiều điểm để kết quả nội suy được chính xác, sát với thực tế.

CHƯƠNG 3: KẾT QUẢ VÀ THẢO LUẬN‌

3.1. Kết quả tính toán chỉ số Kappa‌

Kết quả tính toán chỉ số cán cân nước Kappa tại trạm Vĩnh Yên (Bảng 3.1 và Hình 3.1) cho thấy thời kỳ khô hạn của các năm chủ yếu rơi vào khoảng thời gian từ tháng 11 năm trước cho đến tháng 5 năm sau. Cá biệt có những năm có giai đoạn khô hạn kéo dài gần như cả năm như 1991, 1998. Số liệu thống kê ghi nhận có những năm tình trạng khô hạn kéo dài qua nhiều năm như tư 1995 đến 1998. Nếu chỉ tính từ tháng 1 đến tháng 3 là thời kỳ căng thẳng về nhu cầu nước cho nông nghiệp thì tình trạng khô hạn nhất xảy ra vào các năm 1986, 1991, 2006, 2010... trong khi nếu xem xét cả mùa khô (tháng 12 đến tháng 5 năm sau) thì số năm bị khô hạn nhiều hơn, thêm các năm 1989, 1998, 1999 và chỉ số Kappa cũng có xu thế cao hơn nhiều (Hình 3.2).

Bảng 3.1 Kết quả tính chỉ số Kappa trạm Vĩnh Yên‌

NĂM

T1	T2	T3	T4	T5	T6	T7	T8	T9	T10	T11	T12
1985	1.5	1.0	1.8	0.5	1.3	0.8	0.6	0.3	0.3	0.6	0.8	25.3
1986	8.6	5.2	8.2	0.3	0.4	0.5	0.5	0.6	0.6	1.0	1.4	4.2
1987	3.8	7.1	2.4	0.5	0.7	0.6	0.3	0.3	0.5	0.4	0.4
1988	2.1	0.9	2.0	5.1	0.5	0.5	0.4	0.2	0.9	0.2	6.2	64.9
1989	0.7	2.6	0.6	1.9	0.2	0.3	0.3	0.5	0.8	0.2	7.4	11.5
1990	3.5	0.5	0.4	1.2	0.4	0.3	0.2	1.1	1.1	0.6	15.0
1991	4.8	17.9	0.6	1.3	0.6	0.2	0.2	0.4	1.2	2.7	0.8	3.3
1992	1.4	1.3	2.4	1.6	1.0	0.2	0.3	0.9	0.6	74.1	2.7	1.7
1993	5.0	1.4	1.6	2.0	0.3	0.8	0.4	0.2	0.2	2.2	2.7	9.1
1994	7.8	1.3	0.4	1.7	0.2	0.1	0.1	0.2	0.3	0.7	6.0	1.2
1995	1.2	4.2	1.5	1.7	1.0	0.4	0.3	0.2	0.9	1.2	1.3	23.6
1996	4.7	6.8	0.3	1.0	0.5	0.4	0.2	0.2	0.6	0.8	0.3	7.6
1997	1.7	7.7	0.4	0.3	1.1	0.7	0.1	0.2	0.8	0.4	12.1	6.3
1998	7.5	6.9	1.4	3.1	1.1	0.3	0.8	1.5	1.2	1.6	16.1	5.2
1999	4.1	9.6	7.0	0.9	0.4	0.3	0.5	0.3	1.2	0.2	0.5	0.7
2000	4.0	1.2	1.5	1.3	0.5	0.7	0.3	0.4	0.9	0.3	12.3
2001	2.9	1.6	0.4	0.7	0.8	0.2	0.3	0.2	0.6	0.7	2.4	3.5
2002	1.8	3.3	8.7	2.2	0.4	0.3	0.4	0.4	0.4	0.7	1.2	1.3

T1	T2	T3	T4	T5	T6	T7	T8	T9	T10	T11	T12
2003	1.0	2.3	1.0	0.8	0.8	0.4	0.4	0.1	0.3	1.6	84.3	10.9
2004	1.3	2.4	1.8	0.4	0.6	0.5	0.3	0.4	1.4	12.1	3.5	1.9
2005	3.6	1.4	1.0	0.7	2.3	0.6	0.3	0.3	0.3	2.5	0.7	1.7
2006	19.5	0.2	0.9	1.7	0.4	0.2	0.2	0.1	0.5	1.6	0.5	6.3
2007	5.4	0.8	0.1	0.6	1.1	0.3	0.2	0.2	0.3	1.0	12.7	2.5
2008	1.6	1.5	1.4	1.0	0.2	0.3	0.3	0.2	0.3	0.2	0.2	5.5
2009	9.3	3.9	0.9	0.5	0.3	0.7	0.2	0.7	1.1	0.6	32.4	26.3
2010	0.8	19.6	4.4	1.6	0.6	0.6	0.2	0.2	0.2	2.3	12.6	2.2

NĂM

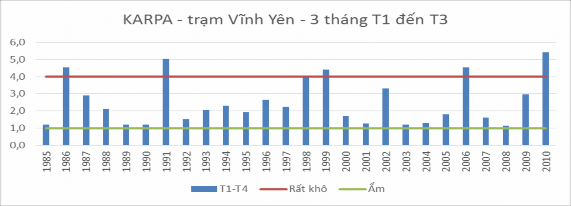
Hình 3.1 Kết quả tính Kappa trạm Vĩnh Yên T1 đến T3‌

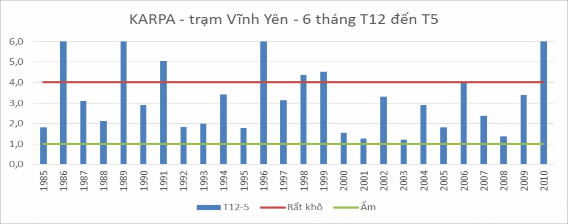
Hình 3.2 Kết quả tính Kappa trạm Vĩnh Yên T12 đến T5‌

Nếu như tình trạng khô hạn kéo dài được tìm thấy ở trung tâm vùng nghiên cứu thông qua số liệu thực đo tại trạm Vĩnh Yên thì số liệu thống kê tại trạm Tam Đảo cho thấy khu vực sường núi phía Tây Bắc vùng nghiên cứu giáp với tâm mưa Tam Đảo có lượng nước đến khá dồi dào, thể hiện qua chỉ số Kappa của hầu hết các năm ở dưới

ngưỡng ẩm ướt. Thời kỳ khô hạn cũng rất ngắn, thường chỉ từ đầu tháng 11 năm trước đến tháng 3 năm sau.

Như vậy có thể thấy lượng nước đến từ mưa và tổn thất từ bốc hơi phân bố rất không đều trong vùng nghiên cứu LVS Phan – Cà Lồ.

Bảng 3.2 Kết quả tính chỉ số Kappa trạm Tam Đảo‌

NĂM

T1	T2	T3	T4	T5	T6	T7	T8	T9	T10	T11	T12
1985	0.2	0.1	0.3	0.2	0.3	0.2	0.2	0.1	0.2	0.2	0.2	10.2
1986	4.3	0.8	6	0.1	0.1	0.2	0.1	0.2	0.1	0.3	0.9	1.1
1987	0.6	0.3	1.7	0.1	0.3	0.2	0.2	0.1	0.1	0.3	0.3	144
1988	0.3	0	1.1	0.5	0.3	0.2	0.3	0.1	0.4	0.1	3.7	6.5
1989	0.3	0.9	0.1	0.8	0.1	0.1	0.1	0.2	0.4	0.2	1.9	2.1
1990	0.3	0.1	0.2	0.3	0.2	0.1	0	0	0.1	0	0	2.3
1991	0.1	1.9	0	0.3	0.3	0.1	0.1	0.2	0.7	0.6	0.4	0.8
1992	0.5	0.3	0.4	1	0.2	0	0.1	0.5	0.2	14.4	1	0.8
1993	1.3	0.4	0.6	0.4	0.1	0.2	0.1	0.1	0.2	1	0.8	2.6
1994	1.3	0.2	0.2	0.2	0.2	0.1	0	0.1	0.1	0.4	3	0.4
1995	0.5	1	0.5	0.1	0.2	0.1	0.1	0.1	0.3	0.7	0.8	15.9
1996	1.2	2.4	0.2	0.3	0.2	0.1	0.1	0.1	0.3	0.9	0.2	6.5
1997	0.7	1.4	0	0.2	0.6	0.2	0	0.1	0.3	0.1	3.2	0.7
1998	1.2	2	0.3	0.4	0.4	0.2	0.3	0.2	0.2	0.5	5	3.8
1999	1.6	1.1	2	0.2	0.1	0.2	0.2	0.1	0.2	0.2	0.2	0.7
2000	0.8	0.3	0.3	0.8	0.2	0.2	0.1	0.2	0.2	0.1	3	5.3
2001	0.4	0.2	0.2	0.3	0.2	0.1	0	0.1	0.4	0.2	1.4	1.7
2002	1.7	0.3	0.5	0.4	0.2	0.1	0.1	0.1	0.3	0.4	0.6	0.3
2003	1	0.2	2.1	0.5	0.2	0.3	0.1	0.1	0.2	0.8	64.6	10.1
2004	0.6	1.1	0.5	0.2	0.1	0.4	0.1	0.1	0.4	27.3	1.2	3.4
2005	1.9	0.4	0.5	0.7	0.6	0.1	0.1	0	0.1	1.8	0.5	1
2006	3.5	0.1	0.3	0.9	0.3	0.1	0.1	0.1	0.2	1.1	1	4.1
2007	4.5	0.4	0.1	0.5	0.8	0.2	0.3	0.2	0.2	0.3	4.3	0.6
2008	0.9	1.1	0.6	0.2	0.2	0.1	0.1	0.1	0.1	0.1	0.2	4.1