Tính Bộ Hấp Thụ Dao Động Thụ Động Cho Hệ Chính Có Cản Nhớt.

Theo [16]

p() được xác định như sau:

det M

p(λ) 1 det Mλ2Cλ K 

(1.39)

Từ (1.9) và (1.39) ta có

p() là:

Có thể bạn quan tâm!

• Tổng Quan Nghiên Cứu Giảm Dao Động Xoắn Và Các Phương Pháp Xác Định Tham Số Tối Ưu
• Mô Hình Bộ Hấp Thụ Dao Động Dạng Con Rãnh Trượt Tròn.
• Một Số Bộ Thông Số Tối Ưu Của Bộ Hấp Thụ Dao Động Thụ Động Cho Hệ Một Bậc Tự Do Không Cản Chịu Kích Động Ồn Trắng.
• Tính Toán Tham Số Tối Ưu Trong Trường Hợp Hệ Chính Có Nhiều Bậc Tự Do
• Mô Phỏng Số Dao Động Xoắn Của Trục Máy Có Lắp Bộ Hấp Thụ Dva.
• Nghiên Cứu, Phân Tích, Tính Toán Và Xác Định Các Tham Số Tối Ưu Của Bộ Hấp Thụ Dao Động Dva

Xem toàn bộ 153 trang tài liệu này.

1 2 3 4

P4a 3a 2a a

(1.40)

trong đó

1 2

a  21,

a 1212,

a  23,

a 24

(1.41)

3 4

Mục tiêu của việc nghiên cứu là tìm các thông số tối ưu , của bộ TMD sao cho cực

của

P có

Re i

 max ,



i  1,..4

(1.42)



Imi min,

i 1,..4

(1.43)

Xét đa thức p() , theo vào định lý Vieta, ta có:

4

Reia1 2 1

i1

(1.44)

Biểu thức này dẫn tới hai bất đẳng thức



1

min Re i (1.45)

i1,..42

4

 Re(i)  min (Re(i ) a1  4 min (Re(i ) 

i 1

(1.46)

Ta có thể thấy rằng vế phải của (1.45) không phụ thuộc vào độ cứng lò xo k1. Do vế trái của (1.46) lại phụ thuộc vào độ cứng của lò xo k1, để bậc của sự ổn định lớn và

dao động tắt nhanh thì độ lớn của các phần thực là lớn nhất có thể nên trong bước đầu tiên hệ số lò xo của bộ hấp thụ dao động TMD được chọn để (1.45) trở thành đẳng thức. Khi (1.45) trở thành đẳng thức thì vế phải của (1.46) triệt tiêu, dẫn tới tất cả các phần thực bằng nhau. Ta ký hiệu giá trị chung đó là 0. Khi đó các trị riêng của hệ là hai cặp phức liên hợp được ký hiệu là 1,2 = 0i1 và 3,4 =0i2, trong đó 1 và 2 tương ứng

là các phần ảo. Vậy đa thức p() là:

p() 2222

0 1 0 2

0 1 2

p() 4 40362222

43  22 2 2 2 2 2 

(1.47)

0 0 1 2 

0 1 0 2

Từ biểu thức (1.45, 1.46) và (1.47) ta thu được hệ phương trình sau:

40  21(1.48)

0 1 2

622212 12

(1.49)

43  22 2  223

(1.50)

Từ (1.48) suy ra:

0 0 1 2

0 1 0 2

2 2 2 2 24

(1.51)

40

21

(1.52)

Thay  từ (1.52) vào (1.50) ta có:

22

2 2 

2 1 2

(1.53)

Từ (1.51) suy ra:

0 12

2 

2 2 2 2 

0 1 0 2

4

(1.54)

Thay (1.53, 1.54) vào (1.49) ta có:

2

2 2 

2 2 2 2 

6 

1 2 2 2 1

0 1 0 2

12

(1.55)

1

2 1 2 

4 



Biến đổi biểu thức (1.55), chúng ta thu được biểu thức quan hệ giữa các phần ảo 1 và

2.

1 2

62  2 1 2 2 1 2

1 2



2 2 2 2 2 2 

(1.56)







1 

1 2

2 1 

1 2 2

2 



Ta sử dụng bất đẳng thức sau:

2

2 2 2

2 2 

2 2

1 2 

1 2 

(1.57)

12 12 1



Từ biểu thức (1.56) và (1.57) ta thu được bất đẳng thức sau:

2 2

42

1 2 

21

(1.58)

 max 2 

4 2

(1.59)

i1,2i

41

Vế phải của biểu thức (1.59) không phụ thuộc vào hệ số cản nhớt c1 của bộ hấp thụ dao động TMD, bởi vì chúng ta muốn độ lớn của phần ảo là nhỏ nên trong bước thứ hai hệ số cản nhớt của bộ hấp thụ dao động c1 được chọn để biểu thức (1.59) trở thành đẳng thức, nghĩa là 1=2.

Giá trị của chúng là:



1 2 

(1.60)

4

4 1

Thay (1.60) vào (1.53) ta có:



1



0 2

(1.61)

Thay (1.60, 1.61) vào (1.54) ta có tham số tối ưu thứ nhất:

* 

1

1

(1.62)

Thay (1.61, 1.62) vào (1.52) ta có tham số tối ưu thứ hai:



1

* 

(1.63)

Phương pháp cực tiểu hóa năng lượng [63], [64].

Xét phương trình vi phân (1.9a), ta đưa về dạng như sau:

•• •

MxDxkx F (1.64)



Với điều kiện đầu

x(0) x0; x(0) x0

Trong đó M, D, K tương ứng là các ma trận khối lượng, cản và độ cứng. Ta dùng phép đổi biến số, từ phương trinh (1.64) đưa về phương trình:



z Vz F (1.65)

V là ma trận sau

0 In 



V = 

(1.66)

M1K M1D



Với In là ma trận đơn vị cấp n. Với điều kiện đầu: z(0) = z0

Phương pháp cực tiểu hóa năng lượng để giảm dao động tần số riêng của kết cấu nên ta xét phương trình vi phân dao động tự do ứng với (1.65)



z Vz (1.67)

Nghiệm của (1.67) có dạng

z eVtz0

Năng lượng toàn phần của hệ là tổng động năng và thế năng được tính bởi công thức.

1 T 1T

Chú ý rằng

Trong đó

E(t, x0, x0) E(t, z0) 2 x(t)

1 z(t)T Q0z(t) E(t, z0 ) 2

Mx(t) x(t)

2

Kx(t)

(1.68)

(1.69)

0 M

Q K 0 

0 

(1.70)

Năng lượng toàn phần của hệ trong suốt quá trình dao động được tính như sau:



E(t, z0 )dt

0

(1.71)

Như vậy tiêu chuẩn thiết kế tối ưu được đặt ra là cực tiểu tích phân năng lượng (1.71). Để có được kết quả rõ ràng hơn ta thực hiện các phép biến đổi như sau:

1 T

1 T

VTt Vt 1T

E(t, z0 )dt 2 z(t, z0 ) Q0z(t, z0 ) dt 2 z0 e

Q0e z0 dt 2 z0 Pz0

0 0 0

Trong đó

(1.72)



P e

0

VTt

Q0eVtdt

(1.73)

Ma trận P là xác định dương. P là nghiệm của phương trình Lyapunov sau:

VT P PV Q0

(1.74)

Trong nhiều trường hợp, ta không cần phải cực tiểu hóa toàn bộ năng lượng của hệ mà chỉ cần giảm một phần nào đó. Khi đó hàm mục tiêu không phải là cực tiểu năng lượng toàn phần trong quá trình dao động của hệ. Thay vào đó một hàm mục tiêu có dạng khác

được đưa ra với mục đích là chỉ cực tiểu một phần năng lượng của hệ tùy theo mục đích thiết kế.



P e

0

VTt

QeVtdt

(1.75)

trong đó Q được hiểu là hàm trọng số, Q đối xứng (thường là bán xác định dương). Tùy thuộc vào thành phần năng lượng cần tính mà Q được chọn sao cho phù hợp. Khi đó P sẽ là nghiệm của phương trình Lyapunov sau:

VT P PV Q  0

Điều này có thể dễ dàng chứng minh được như sau:

(1.76)

1 T

1 T T

E(t, z0 )dt 2 z Qz dt 2 z

0 0 0

(V P PV)z dt



1 T T T 1 T T

 (z V Pz z PVz) dt  (Vz) 2 0 2 0

Pz z PVz) dt

1d



(zT Pz) dt 1

zT Pz



0 0

1zT Pz

2 dt

0

2 0 2

Kết luận: Các tham số tối ưu α và được tìm làm cực tiểu hàm mục tiêu.

L 1 zT Pz (1.77)

2 0 0

Trong đó z0 là điều kiện ban đầu, P là nghiệm của phương trình đại số Lyapunov (1.76). Để cực tiểu hàm mục tiêu L, điều kiện cực tiểu của hàm hai biến được áp dụng vào (1.77).

L



*

 0,

 0

L



*

(1.78)

Giải hệ phương trình (1.78) tìm tham số tối ưu cho TMD là:

*  1 ,

1

* 

(1.79)



1

Ta thấy rằng với cùng một kết cấu như nhau thì tham số tối ưu tìm được theo các phương pháp khác nhau là không giống nhau. Vì mỗi một phương pháp áp dụng cho cơ hệ chịu lực kích động khác nhau. Vì vậy khi tìm tham số tối ưu của bộ hấp thụ dao động TMD, ta phải xem hệ chính chịu kích động của loại lực nào để áp dụng phương pháp tìm tham số tối ưu thích hợp.

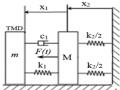
1.2.4. Tính bộ hấp thụ dao động thụ động cho hệ chính có cản nhớt.

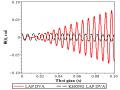
Xét cơ hệ có lực cản nhớt c2x2được mô tả trên hình 1.1 chịu kích động điều hoà, biểu thức tương tự (1.6) mô tả A cũng có thể được xác lập, tuy nhiên các điểm không thay đổi S, T đã nói ở trên không tồn tại. Vì vậy để giải bài toán trên người ta phải sử dụng phương pháp số để xác định cặp giá trị tối ưu của , . Một hướng nghiên cứu

được thực hiện bởi Randall và các cộng sự (1981) là chọn giá trị tối ưu của ,bằng cách làm nhỏ nhất hai đỉnh của đường cong biên độ mô tả trên hình 1.3 bằng phương pháp số. Những giá trị tối ưu của ,cho những trường hợp 2 nhỏ cũng được tổng kết bởi Ioi và Ikeda [36] theo công thức sau:

opt



opt



 (0.2411.7 2.62 )

 (0.13 1.2 0.42 )

 (1.0 1.92 )2

2 2

 (0.01 0.9 32 )2

(1.80)

opt opt 2 2

ở đây 2 là tỷ số cản nhớt của hệ chính.

Độ chính xác và khoảng sai số cho các công thức trên nhỏ hơn 1% trong khoảng

0.03  0.4 và 0.01 2  0.15 , đây cũng là khoảng tỉ số khối lượng và cản nhớt

thường gặp trong thực tế.

Phương pháp xác định tần số được đưa ra bởi Thompson [58] cũng để xác định α, ξ cho hệ chính có cản nhớt. Theo cách tính này α được xác định theo phương pháp số và ξ có thể được xác định bằng giải tích khi đã biết α.

Warburton (1982) [67] xác định các thông số tối ưu của bộ hấp thụ dao động thụ động dạng khối lượng cho hÖ một bậc tự do cho các trường hợp kích động là điều hoà và ngẫu nhiên tác động vào hệ chính ở dạng ngoại lực hoặc gia tốc nền. Warburton đã tính đạo hàm của đáp ứng hệ chính theo các tham số của bộ TMD và cho các đạo hàm này bằng không dẫn tới việc giải các phương trình phi tuyến. Việc giải được thực hiện trên máy tính và cho kết quả số.

Những năm gần đây, GS Nguyễn Đông Anh và các cộng sự [20] áp dụng ý tưởng của phương pháp tuyến tính hóa tương đương và tiêu chuẩn sai số bình phương trung bình để thu được xấp xỉ hệ chính không cản từ hệ chính ban đầu có cản để có thể dễ dàng hơn trong việc tìm lời giải (giải tích) cho các tham số tối ưu của TMD.

Phương pháp tuyến tính hóa tương đương cho hệ tiền định được đề xuất bởi Krylov và Bogoliubov (1943). Sau đó Caughey (1956, 1960) mở rộng phương pháp để áp dụng cho hệ ngẫu nhiên [20].

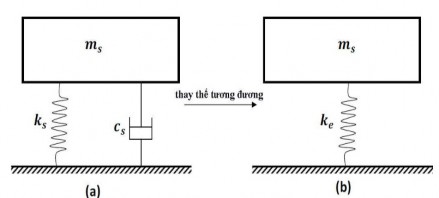
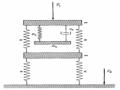
Hình 1.10. Sự xấp xỉ hệ chính [20].

Trong hình 1.10a, mô tả hệ chính có cản ban đầu, phương trình vi phân chuyển động có dạng:

x  2x 2 x  0

(1.81)

s s s s s s

Trong hình 1.10b, hệ không có cản, phương trình vi phân chuyển động có dạng

x 2 x  0

(1.82)

s e s

Trong đó e là tần số tương đương.

Xem tất cả 153 trang.