Một Số Bộ Thông Số Tối Ưu Của Bộ Hấp Thụ Dao Động Thụ Động Cho Hệ Một Bậc Tự Do Không Cản Chịu Kích Động Ồn Trắng.

(2 2 )

(22)(12) 22

1

1 2 1



Giải phương trình trên ta nhận được:

2 

1112 124 221

1,2

2 

Trong đó β1 (lấy dấu -) là hoành độ của điểm S, β2 (lấy dấu +) là hoành độ của điểm T. Biểu thức xác định tung độ của S và T có dạng :

AS 

1

1

1  (1 )2

AT 

1

2

1  (1 )2

Do β1 và β2 là hàm của các tham số và α nên các tung độ của các điểm S và T phụ thuộc vào và α và do vậy phụ thuộc vào các khối lượng m, M và các hệ số độ

cứng k2 và k1 .

1

Vì ta đã biết trước M và k2 nên nếu ta chọn m thì chỉ còn lại hệ số α là cần phải xác định để thoả mãn điều kiện tung độ S và T bằng nhau. Giá trị tối ưu của f tìm được bằng cách giải phương trình AS= AT. Sau khi giải ta tìm được:

opt

 1

(1.11)

Với giá trị tìm được của α opt , hÖ sè A, β1 và β2 tại hai điểm S và T bằng

12



A 

(1.12)



2 



2 1 1  

1,2 1 

Tiếp theo ta tìm hệ số cản để đường cong biên độ tần số đạt cực đại tại các điểm S và T.

Ta thay các giá trị tìm được của α

opt , β1

và β2

vào phương trình

A  0



và thực

hiện một vài phép biến đổi ta nhận được hệ thức giữa tham số và :



2 

 3 



Tại S :

2 



813



2 

 3 



Tại T :

2 



813

3

8(1 )3

Theo Brock [24] giá trị tốt nhất của opt có thể chọn bằng trung bình cộng của hai giá trị cản tối ưu tìm được tại hai điểm S và T trên và bằng

opt 

(1.13)

Nhìn vào biểu thức (1.13) ta thấy rằng khi chọn được bộ hấp thụ dao động tối ưu hiệu quả của bộ hấp thụ dao động tỷ lệ nghịch với hệ số hay nói cách khác việc tăng khối lượng của bộ hấp thụ dao động làm giảm biên độ dao động lớn nhất của hệ chính.

Cũng theo phương pháp này Warburton [67] đã tính toán được các thông số tối ưu của bộ hấp thụ dao động thụ động cho một số dạng của kích động điều hòa. Kết quả tính toán được trình bày trong bảng 1.1. Ở trường hợp thứ nhất, lực kích động tuần hoàn tác động vào hệ chính, tiêu chuẩn tối ưu là cực tiểu biên độ dao động của hệ chính. Ở trường hợp thứ hai, lực kích động tuần hoàn tác động vào hệ chính, nhưng tiêu chuẩn tối ưu là cực tiểu biên độ gia tốc của hệ chính.

Trong trường hợp cuối cùng, hệ chịu kích động của gia tốc nền, tiêu chuẩn tối ưu là cực tiểu biên độ gia tốc của hệ chính. Trường hợp hệ dao động mô tả ở trên chịu lực kích động ồn trắng cũng đã được xét trong nghiên cứu của Warburton [67] với giả thiết hệ chịu kích động ồn trắng với mật độ phổ So.

Bảng 1.1. Các thông số tối ưu của bộ hấp thụ dao động cho cơ hệ một bậc tự do không có cản ( Xg là gia tốc nền)

Dạng Kích động

Tiêu chuẩn tối ưu (A)	Thông số tối ưu
	Aopt	αopt	opt
i t P 0 e	kx 2 P0	 2 1/ 2 1 	1 1 	3 8(1 )
i t P 0 e	m2x2 P0	 21/ 2  1	 11/ 2  1	3 8(1  / 2)
Xeit g	Xx g 2 X g	 2 1/ 2 1 	1 1 	3 8(1 )

Có thể bạn quan tâm!

• Nghiên cứu giảm dao động xoắn của trục máy bằng bộ hấp thụ dao động - 2
• Tổng Quan Nghiên Cứu Giảm Dao Động Xoắn Và Các Phương Pháp Xác Định Tham Số Tối Ưu
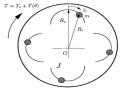
• Mô Hình Bộ Hấp Thụ Dao Động Dạng Con Rãnh Trượt Tròn.
• Tính Bộ Hấp Thụ Dao Động Thụ Động Cho Hệ Chính Có Cản Nhớt.
• Tính Toán Tham Số Tối Ưu Trong Trường Hợp Hệ Chính Có Nhiều Bậc Tự Do
• Mô Phỏng Số Dao Động Xoắn Của Trục Máy Có Lắp Bộ Hấp Thụ Dva.

Xem toàn bộ 153 trang tài liệu này.

Bảng 1.2. Một số bộ thông số tối ưu của bộ hấp thụ dao động thụ động cho hệ một bậc tự do không cản chịu kích động ồn trắng.

Dạng Kích động

Tiêu chuẩn tối ưu (A)	Thông số tối ưu
	Aopt	opt	opt
Lực (ồn trắng)	x 2 P 2 2 2So	1  4  32   4(1 ) 	1 / 2 1
					1  3/ 4 41 / 21 
Gia tốc nền (ồn trắng)	x2 2 1 2So	1 1 321 1  2 4  	1  / 2 1 
					1 / 4
					41 / 21 

Tiêu chuẩn để chọn thông số tối ưu của bộ hấp thụ dao động thụ động là cực tiểu

2

trung bình bình phương của chuyển vị của hệ chính

x2(t)

. Để tìm được các thông số

tối ưu, giá trị của

x2(t)

được tìm như một hàm phụ thuộc vào các tham số α, . Sau

2

x

2

đó cho 2

/  0 và

2 /  0 và giải hệ hai phương trình hai ẩn số này để tìm

x

2

giá trị của α, ξ.

Bằng phương pháp này, Warburton đã xác định được các thông số tối ưu của bộ TMD cho hệ dao động một bậc tự do không có cản nhớt.

Kết quả này được đưa ra trong bảng 1.2 cho hai trường hợp: trường hợp một, hệ chịu lực kích động tác động vào hệ chính, tiêu chuẩn tối ưu là cực tiểu trung bình bình phương của chuyển vị của hệ chính, trường hợp hai, hệ chịu lực kích động của gia tốc nền và tiêu chuẩn tối ưu là cực tiểu trung bình bình phương của chuyển vị của hệ chính.

Phương pháp cực tiểu mô men bậc hai.

Phương pháp cực tiểu mô men bậc hai áp dụng cho lực kích động ồn trắng F(t) có cường độ Sf. [67]

Từ phương trinh (1.9) ta đưa về phương trình trạng thái sau:

y (t) By H f F(t)

Trong đó y(t) là véc tơ trạng thái ứng với các đáp ứng của hệ:

(1.14)

y  [x x

T

2 1 x2

x1 ]

(1.15)

B là ma trận hệ thống



 0 0 1 0 

B =



 0 0 0 1 

2 2



a

0 2a 

(1.16)



2  (1)2 0  2(1)

a a 

Còn Hf là ma trận định vị của kích động

H f  [0 0 1 / M

1 / M ]T

(1.17)

Ma trận mô men bậc hai P là nghiệm của phương trình ma trận Lyapunov:

BP PBT

S f H f HT  0

(1.18)

f

Sau khi tìm được ma trận mô men bậc hai P. Ta có kết quả mô men bậc 2 của chuyển dịch của hệ chính là [61], [62], [66]:



f

141 2242 42 2S

P

(1.19)

11 4

3M 2

Các tham số tối ưu α và được tìm làm tối ưu mô men bậc hai của đáp ứng hệ chính P11. Điều kiện cực tiểu là:

P11



*

 0,

 0

P11



*

(1.20)

(3 4)21 2

Như vậy để thu được tham số tối ưu với chỉ tiêu cực mô men bậc hai thì ta cần giải hệ (1.19, 1.20) được kết quả như sau:

*  2 4;

2(1 )

* 

(1.21)

Phương pháp cực đại độ cản tương đương.

Phương pháp cực đại độ cản tương đương được sử dụng khi kết cấu dao động ngẫu nhiên chịu kích động ồn trắng (Luft 1979 [39]). Trước hết ta cần xác định lực do bộ hấp thụ dao động TMD tác động vào hệ chính.

Xét hệ phương trình (1.9). Nhân hàng thứ 2 với -1 rồi cộng với hàng thứ nhất, sau đó nhân với M ta có:



M x2 M 2



x2  2mx1M 

22

x1 F (t)

(1.22)

Vậy lực cản do bộ TMD tác động vào hệ chính là:



F  2m

M 22 x

x1 1

(1.23)



F x2



x2

2

2mx1 x2 M 22 x







1 x2



x2

Khi đó hệ số cản tương đương của bộ TMD tác động vào hệ chính là:

ctd

(1.24)

Nếu xét hệ kích động là ồn trắng, các giá trị trung bình trong (1.24) là các thành phần của ma trận mô men bậc hai P trong phương trình ma trận Lyapunov [39].



F x2



x2

2

2mP M 22P

ctd

34 32

P33

(1.25)

Để cực đại ctd, điều kiện cực đại của hàm hai biến được áp dụng vào (1.25).

ctd



*

 0,

 0

ctd



*

(1.26)

Giải hệ phương trình (1.25, 1.26) tìm tham số tối ưu cho TMD là:

1 

*  1 ,

* 



2

(1.27)

Phương pháp cân bằng cực.

Phương pháp cân bằng cực được sử dụng khi làm giảm dao động tần số riêng của hệ (dao động rung lắc) [8], [19]. Ta chuyển hệ phương trình vi phân cấp 2 (1.9) về phương trình vi phân cấp 1 bằng cách đặt như sau:

x2 s1, x1 s2



(1.28)

x2 s3, x1 s4

Khi đó ta có hệ phương trình vi phân tuyến tính thuần nhất bậc 4:



s(t) As(t)

(1.29)

Hệ (1.29) luôn luôn tồn tại một hệ cơ bản 4 véc tơ nghiệm độc lập tuyến tính

i (t) , i=14. Nó trùng với 4 véc tơ đơn vị ei khi t=0, (0) ei ,

Và thoả mãn điều kiện (1.29)

i  1, 4.



φ(t) Aφ(t)

Các véc tơ nghiệm sẽ tạo thành các cột của ma trận không suy biến 44

Φ(t) 1(t) | 2 (t) | 3 (t) | 4 (t)

(1.30)

(1.31)

Ma trận (1.31) được gọi là ma trận cơ bản, nó có một số tính chất đặc trưng, đây là véc tơ nghiệm đặc biệt được chuẩn hoá tại thời điểm ban đầu t=0, thì vấn đề trị riêng đặc trưng cho dáng điệu của hệ động lực (1.29) theo các nghiệm riêng với tính chất là



véc tơ trạng thái s(t) và đạo hàm của nó s(t)

có cùng hướng trong không gian trạng thái



s(t) s(t)

(1.32)

Nếu các nghiệm riêng này tồn tại, khi đó chúng phải thoả mãn không chỉ phương trình (1.29) mà còn cả điều kiện (1.32). Điều này nói lên rằng các quỹ đạo mà giữ nguyên hướng không đổi trong không gian trạng thái phải thoả mãn

s(t)  ets(1.33)

Điều này phù hợp với điều kiện (1.32). Thay (1.33) vào (1.32) ta có

etsAets(1.34)

Ta được phương trình thuần nhất

E A s 0

Mà được gọi là bài toán trị riêng liên quan với ma trận A

(1.35)

Bài toán trị riêng (1.35) có nghiệm véc tơ không tầm thường s nếu và chỉ nếu

E A 

là ma trận suy biến. Một cách chính xác, đó là trường hợp khi là nghiệm

của đa thức

1 2 3 4

p()  det(E A) 4 g 3 g 2 g g

(1.36)

đa thức p() được gọi là đa thức đặc trưng của hệ (1.35)

Ta nhận thấy rằng toàn bộ hệ cũng như các giá trị riêng đều phụ thuộc vào đa thức đặc trưng này, ứng với phương trình đặc trưng (1.36), các giá trị riêng có dạng i

= iii, i=14. Các giá trị riêng này có chứa các thông số của bộ hấp thụ dao động. Nếu hệ dao động ổn định với một số tổ hợp tham số chấp nhận được, Re i  0, i  1 4 . Giá trị riêng của đa thức đặc trưng đầu tiên sẽ được xem xét là bậc của sự ổn định (dự trữ ổn định tuyệt đối), được xác định là khoảng cách đo từ trục ảo tới trị riêng gần nhất.

d0  maxRe i 

i1,4

(1.37)

Bậc của sự ổn định đặc trưng cho tốc độ tắt dần của quá trình chuyển tiếp. Nếu bậc của sự ổn định lớn khi đó các dao động riêng sẽ tắt nhanh. Giá trị riêng phức liên hợp i = iii, i <0, có thể xác định bậc của sự tắt dần (dự trữ ổn định tương đối ).





i 

D  max Re i

0 i1,4

(1.38)

i

2 2

i

i

Bậc của sự tắt dần là chỉ số tắt dần nhỏ nhất

Di 

, i  1 4

của các dao động riêng khác nhau, và nó biểu thị sự giảm của độ lệch ban đầu theo số chu kỳ, nếu bậc của sự tắt dần là lớn thì dao động sẽ tắt sau vài chu kỳ và bậc của sự tắt dần càng lớn thì dao động sẽ tắt càng nhanh. Bậc của sự tắt dần lớn cũng bảo đảm biên độ dao động nhỏ và do đó sẽ có dáng điệu ít nhiễu hơn.

Các nghiệm của đa thức đặc trưng (1.36) gọi là các cực của hệ thống. Từ (1.37, 1.38) ta có nhận xét: Nếu như hệ làm ổn định thì các cực của hệ phải có phần thực âm, nghĩa là chúng nằm trên nửa trái của mặt phẳng phức, phần thực của các cực sẽ thể hiện độ tắt dần của đáp ứng, còn phần ảo thể hiện số lần dao động thực hiện. Mà mục đích của việc thiết kế bộ hấp thụ dao động TMD là làm dao động của hệ chính tắt càng nhanh càng tốt. Vì thế quá trình tính toán tìm các thông số của bộ hấp thụ dao động là tìm các hệ số để độ lớn của các phần thực của các cực càng lớn càng tốt và độ lớn của phần ảo của các cực càng bé càng tốt.