Nghiên Cứu, Phân Tích, Tính Toán Và Xác Định Các Tham Số Tối Ưu Của Bộ Hấp

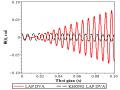
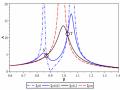
đáng kể so với trường hợp khi chưa lắp DVA. Điều này cũng xảy ra tương tự trong trường hợp hệ chịu kích động ngẫu nhiên được thể hiện trên hình 2.5.

Từ những phân tích kể trên tác giả nhận thấy rằng: Việc xác định các thông số của bộ hấp thụ dao động DVA là rất quan trọng để tăng hiệu quả giảm dao động xoắn cho trục máy. Nếu các thông số thiết kế được chọn không hợp lý, có thể có tác dụng giảm dao động nhưng với hiệu quả thấp (hình 2.4 và 2.5), hoặc không những không mang lại hiệu quả giảm dao động mà còn làm tăng biên độ dao động của loại dao động có hại này. Từ đó ta thấy rằng, việc xác định các thông số tối ưu của bộ hấp thụ DVA để nâng cao hiệu quả giảm dao động xoắn cho trục là một việc làm hết sức ý nghĩa và có ứng dụng thực tế kỹ thuật.

2.4. Kết luận chương 2

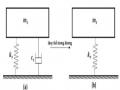
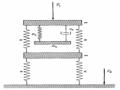
Chương 2 đã thiết lập mô hình cơ học và mô hình toán học để xác định dao động xoắn của trục máy có sử dụng bộ hấp thụ dao động DVA dạng đĩa-cản nhớt-lò xo trường hợp hệ chính có cản và không cản. Để thiết lập hệ phương trình vi phân dao động của hệ, tác giả sử dụng phương trình Lagrange loại II. Hệ phương trình vi phân tìm được là hệ tuyến tính. Từ quy luật dao động xoắn của trục máy, ta nhận thấy rằng nó có chứa các đại lượng thiết kế của bộ hấp thụ dao động DVA, đây chính là cơ sở để các nhà khoa học nghiên cứu, phân tích, tính toán tìm tham số tối ưu của các bộ hấp thụ dao động theo các tiêu chuẩn tối ưu khác nhau.

Cuối chương tác giả mô phỏng số đáp ứng dao động xoắn của trục máy trong trường hợp không lắp và có lắp bộ DVA với thông số được chọn bất kỳ, từ đó thấy rằng việc lắp bộ DVA vào trục máy nó đã có tác dụng làm thay đổi biên độ dao động của trục, tuy nhiên không phải cứ lắp bộ hấp thụ dao động là biên độ dao động của trục máy giảm mà trong trường hợp chọn các thông số của bộ DVA không hợp lý thì không những biên độ dao động của trục máy không giảm mà còn tăng lên. Từ đây tác giả nhận thấy rằng việc nghiên cứu xác định các tham số tối ưu của bộ hấp thụ động lực DVA là hết sức cần thiết và ý nghĩa. Việc tính toán xác định tham số tối ưu này được tác giả trình bày trong chương 3.

CHƯƠNG 3. NGHIÊN CỨU, PHÂN TÍCH, TÍNH TOÁN VÀ XÁC ĐỊNH CÁC THAM SỐ TỐI ƯU CỦA BỘ HẤP THỤ DAO ĐỘNG DVA

Để xác định các thông số tối ưu của hệ thống giảm dao động DVA, ta có nhiều phương pháp khác nhau như: Phương pháp hai điểm cố định, phương pháp cực tiểu mô men bậc hai, phương pháp cực đại độ cản tương đương, phương pháp cân bằng cực, phương pháp cực tiểu hóa năng lượng, phương pháp bình phương tối thiểu, các phương pháp số, … và ứng với mỗi phương pháp khác nhau ta lại tìm được các thông số tối ưu khác nhau của các bộ hấp thụ dao động. Việc áp dụng phương pháp nào để tìm các thông số tối ưu, hoàn toàn phụ thuộc vào đáp ứng dao động của kết cấu mà yêu cầu của thực tiễn kỹ thuật cần giảm dao động.

Trong giới hạn của luận án này, tác giả tìm các thông số tối ưu của các bộ hấp thụ dao động DVA với mục đích là giảm chuyển vị góc của hệ chính (dao động xoắn của trục) với mô hình trục máy không có cản (cs=0). Thông qua việc mô phỏng số (trình bày trong chương 4 của luận án), kết quả sẽ được chứng minh là vẫn có hiệu quả tốt đối với trường hợp hệ chính có cản.

Có thể bạn quan tâm!

Xem toàn bộ 153 trang tài liệu này.

Với mục tiêu là nghiên cứu, tính toán bộ hấp thụ dao động tối ưu để giảm chuyển vị của hệ chính. Các phương pháp tối ưu được sử dụng là trong luận án là:

- Phương pháp hai điểm cố định theo các tài liệu [29], [30], [59] khi trục máy chịu tác động của mô men kích động điều hòa. Mục đích chính của phương pháp này là giảm đỉnh cộng hưởng của biên độ dao động tới giá trị nhỏ nhất có thể.

- Phương pháp cực tiểu mô men bậc hai [60], [67] và phương pháp cực đại độ cản tương đương [39] khi trục máy chịu tác dụng của kích động ngẫu nhiên ồn trắng với mật độ phổ Sf.

- Phương pháp cực tiểu hóa năng lượng [6], [63], [64], với mục đích là thiết kế bộ hấp thụ động lực DVA nhằm giảm thành phần dao động tần số riêng của kết cấu. Bài toán đặt ra là xác định các tham số tối ưu của bộ hấp thụ DVA sao cho phiếm hàm tích phân năng lượng đạt cực tiểu.

Các tham số tối ưu của bộ hấp thụ dao động DVA bao gồm hệ số lò xo và hệ số cản nhớt. Xác định được các tham số này cho phép ta chọn được lò xo và dầu cản nhớt cho thiết kế DVA với hiệu quả giảm dao động tốt nhất mà vẫn đảm bảo các yêu cầu kỹ thuật và kinh tế đặt ra khi thiết kế.

3.1. Xác định tham số tối ưu trong trường hợp trục máy chịu kích động điều hòa

Với lực kích động điều hòa ta sử dụng phương pháp giải tích hai điểm cố định (gọi tắt là FPM-Fixed Points Method) để xác định tham số tối ưu. Trong phần này, tác giả tìm các thông số tối ưu của các bộ hấp thụ dao động DVA với mục đích là giảm chuyển vị của hệ chính (dao động xoắn của trục).

Từ các phương trình vi phân dao động (2.37) và (2.38) ta có tần số dao động riêng của bộ hấp thụ dao động DVA là:



a (3.1)

và tần số dao động riêng của trục máy:

s 

(3.2)

Ta đặt các đại lượng không thứ nguyên như sau:

ma

a

r

là tỷ số giữa khối lượng của bộ hấp thụ và rotor

là tỷ số bán kính quán tính của bộ hấp thụ và rotor

e1

r

là tỷ số vị trí lắp lò xo

e2

r

là tỷ số vị trí lắp bộ cản nhớt

a

s



s

là tỷ số giữa tần số riêng của bộ DVA với trục.

là tỷ số giữa tần số của kích động và tần số riêng của trục

ca maa

là tỷ số cản nhớt của bộ hấp thụ DVA.

Do đó phương trình vi phân dao động (2.25) và (2.26) trở thành:

(1 2)2

2M

(3.3)



a s2

r r

22

n222

ns

2 0

(3.4)

Khi so sánh hệ phương trình vi phân dao động xoắn (3.3), (3.4) với hệ phương trình vi phân dao động (1.9b) của Den Hartog (phần tổng quan thuộc chương 1 của luận án này), tác giả nhận thấy rằng hệ phương trình vi phân (3.3), (3.4) thuộc dạng phương trình chuẩn của Den Hartog. Điều này có nghĩa là việc áp dụng lý thuyết điểm cố định kinh điển cho mô hình trục máy chịu xoắn được nghiên cứu trong luận án là hoàn toàn phù hợp và tin cậy.

Điểm mới và khác biệt trong luận án là ngoài việc luận án tập trung nghiên cứu cho mô hình mới - mô hình trục máy chịu xoắn có lắp bộ hấp thụ dao động DVA thì xét về mặt hệ số của hệ phương trình vi phân có chứa cả những đại lượng không thứ nguyên mô tả vị trí lắp đặt lò xo γ, vị trí lắp đặt bộ cản nhớt λ. Vì vậy trong biểu thức giải tích tối ưu xác định được ngoài việc chứa tỷ số khối lượng μ, còn chứa cả các đại lượng mô tả vị trí lắp lò xo và vị trí lắp bộ cản nhớt. Từ đó cho phép người thiết kế xác định được vị trí lắp đặt lò xo và bộ cản nhớt tối ưu phù hợp với các yêu cầu kỹ thuật và điều kiện lắp ráp đặt ra. Đặc biệt, từ việc tính toán các tham số tối ưu của bộ DVA cho mô hình trục máy có 1 bậc tự do, luận án phát triển phương pháp điểm cố định cho mô hình trục máy có nhiều bậc tự do (mục 4.2 chương 4 của luận án này).

Biểu diễn phương trình (3.3), (3.4) dưới dạng ma trận ta có:

Mq

CqKq F

(3.5)

Trong đó véc tơ tọa độ suy rộng, véc tơ tốc độ suy rộng và véc tơ gia tốc suy rộng lần lượt là:





q 

a 

(3.6)

q  







a 

(3.7)







q  

(3.8)

a 

Và ma trận khối lượng, ma trận cản nhớt, ma trận độ cứng và véc tơ của lực kích động được biểu diễn như sau:

12 2 

M 



C 0

2

2 



0 

(3.9)



n

2 

(3.10)

2 0 



K s

 0

n222 

(3.11)

M (t) 

F m 2 

r r 

(3.12)

0

Xét trường hợp trục máy chịu tác động của mô men kích động tuần hoàn, do hệ thống lắp nối tiếp với trục tác dụng lên. Mô men kích động tuần hoàn tác dụng lên trục được biểu diễn dưới dạng phức như sau:

M (t) MˆeIt

(3.13)

Trong đó:

Mˆlà biên độ phức của kích động tuần hoàn ω là tần số của mô men kích động tuần hoàn

Khi trục máy (hệ chính) chịu tác động của kích động điều hòa thì đáp ứng biên độ của các tọa độ suy rộng được biểu diễn như sau:

ˆe It

(3.14)

It

aˆae

(3.15)

Trong đó:

ˆvà ˆalà biên độ dao động phức của hệ chính và DVA Thay vào phương trình vi phân dao động (3.5) ta thu được

2 2

2 It

2 2 2

It

2 It

Mˆ 2

It 

 (



 1)

se

s ˆ 

se

sˆase

s ˆ 



se s 



22n2eIstˆ

I2n2eIstˆ222eIstˆ222eIstˆ

s a

s a s

s a 

(3.16)

Giải phương trình (3.16) ta thu được biên độ dao động phức của của dao động xoắn hệ chính (trục máy đàn hồi):



s 

ˆ 

I2n22n 22

Mˆ

42 In23(12) n22(12) 22 I2n22n k 

(3.17)

Và biên độ dao động phức của bộ hấp thụ DVA:

ˆDMˆ

a 

(3.18)

E ks 

trong đó:

D 22

E 42 In23(12 ) 

n22 (12) 22 I2n22n

Đặt:

B ( I2n22n 22 )

C 42 In23(12 ) 

n22 (12 ) 2 2 I2n22n

Khi ấy phương trình (3.17) trở thành:

ˆ 

BMˆ

(3.19)

C ks 

Đặt các hệ số

A  Re(B) 22n 22

A 1 Im(B) n2 2 

A  Re(C) 22n22 222n 

22 42 22n

A 1 Im(C) 322n 32n 2n 4 

(3.20)

(3.21)

(3.22)

(3.23)

Do đó đáp ứng bình ổn của hệ chính có dạng:

ˆ 

A1IA2Mˆ

A IA k 

(3.24)

3 4 s 

Nhân cả tử và mẫu của biểu thức (3.24) với

( A3 IA4 ) ta có:

ˆ ( A1IA2)( A3IA4) Mˆ

( A IA )( A I

3 4 3

A4 ) ks 

ˆ 

A1A3IA1A4IA2A3I 22A2A4Mˆ

A2 IA A

IA A

I 22 A2

ks 

ˆ 

3 3 4 3 4 4 

A1A3A2A42I( A2A3A1A4) Mˆ

A2 A22

ks 

3 4

ˆ ( A1A3 A2 A42) 



( A2A3A1A4) Mˆ

A2 A22 I A2 A22

k 

(3.25)

3 4 3 4

s 

Vậy độ lớn thực của đáp ứng ổn định của hệ chính là

Mˆ

A A A A 2 2 A A A A 2

s 3 4

1 3 2 4 2 3 1 4 

A A 

2 2 2

3 4

A A 

2 2 2



ˆ 

Mˆ

A2A2 2A A A A 2A2A24A2A22 2A A A A 2A2A22

1 3

1 3 2 4

2 4

2 3

1 3 2 4

1 4

(A2 A22)2

3 4

ˆ 

Mˆ

A2A2 A2A24A2A22A2A22

1 3 2 4 2 3 1 4

( A2A22)2

3 4

ˆ 

Mˆ

A2( A2A22) A22( A22A22)

1 3 4 2 4 3

( A2A22)2

3 4

ˆ 

Mˆ

( A2 A22)( A2 A22)

1 2 3 4

( A2A22)2

3 4

ˆ 