Tổng Quan Nghiên Cứu Giảm Dao Động Xoắn Và Các Phương Pháp Xác Định Tham Số

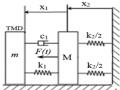
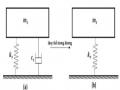
Luận án chỉ tập trung nghiên cứu giảm dao động xoắn của trục máy, không xét đến các dao động khác, chẳng hạn dao động dọc trục, dao động uốn, … Việc tính toán khi kể đến các dao động này được tác giả đề cập trong phần hướng nghiên cứu tiếp theo của Luận án.

4. Phương pháp nghiên cứu.

Trên cơ sở các trục máy trong thực tế, tác giả chuyển về mô hình lý thuyết có lắp bộ hấp thụ dao động DVA. Từ mô hình tính toán của trục máy có lắp bộ DVA, tác giả sử dụng phương trình Lagrange loại II để thiết lập phương trình vi phân dao động của hệ.

Từ hệ phương trình vi phân dao động thu được, tác giả tiến hành nghiên cứu, phân tích tính toán để giảm dao động xoắn cho trục máy, tìm nghiệm giải tích của hệ bằng các phương pháp: Phương pháp hai điểm cố định, phương pháp cực tiểu mô men bậc hai, phương pháp cực đại độ cản tương đương và phương pháp cực tiểu hóa năng lượng.

Để thực hiện các tính toán và đánh giá hiệu quả giảm dao động của kết quả nghiên cứu của luận án tác giả xây dựng các chương trình máy tính trên phần mềm Maple để mô phỏng dao động của hệ để người đọc có cái nhìn trực quan về hiệu quả của bộ hấp thụ dao động. Đây là phần mềm được các nhà khoa học trên thế giới chuyên dùng và cho kết quả tin cậy.

5. Những đóng góp mới của luận án.

- Tính toán tìm được các thông số tối ưu của bộ hấp thụ dao động DVA giảm dao động xoắn cho trục máy có một bậc tự do theo các phương pháp khác nhau. Tham số tối ưu được biểu diễn dưới dạng giải tích tường minh.

- Xây dựng các chương trình tính toán trên phần mềm để đánh giá, so sánh và kiểm chứng sự khác biệt thông qua đáp ứng đầu ra của mô hình mô phỏng trong trường hợp hệ chịu kích động điều hòa, kích động va chạm và kích động ngẫu nhiên với bộ tham số tối ưu.

- Đã phát triển các kết quả nghiên cứu cho trường hợp hệ chính có nhiều bậc tự do. Đưa ra các biểu thức giải tích của tham số trong trường hợp tối ưu cho hệ có 1, 2 và 3 bậc tự do.

Có thể bạn quan tâm!

Xem toàn bộ 153 trang tài liệu này.

6. Bố cục của luận án.

Luận án gồm phần mở đầu, bốn chương và phần kết luận, hướng nghiên cứu tiếp theo với 139 trang, 12 bảng và 45 hình vẽ và đồ thị.

Chương 1 trình bày tổng quan về nghiên cứu giảm dao động xoắn và các phương pháp tính toán xác định tham số tối ưu của bộ hấp thụ dao động.

Chương 2 thiết lập mô hình tính toán và xác định hệ phương trình vi chuyển động mô tả dao động của cơ hê.

Chương 3 giải quyết bài toán tính toán giảm dao động xoắn cho trục máy và xác định tham số tối ưu của bộ hấp thụ động lực DVA theo các phương pháp khác nhau.

Chương 4 phân tích, đánh giá hiệu quả giảm dao động theo các kết quả tối ưu được xác định tại chương 3, mô phỏng số các kết quả nghiên cứu giảm dao động xoắn cho trục máy. Phát triển các kết quả nghiên cứu cho trường hợp trục máy có nhiều bậc tự do.

Các kết quả chính, những đóng góp mới và hướng nghiên cứu tiếp theo của luận án được tóm tắt trong phần kết luận.

Danh sách công trình đã được công bố thuộc luận án bao gồm 06 bài báo, trong đó:

Bài báo số 1 được công bố trên tạp chí Journal of Multibody Dynamics (thuộc danh mục ISI, Impact Factor 1.242).

Bài báo số 2 được công bố trên Tạp chí Khoa học Công nghệ, các Trường Đại học Kỹ thuật, ISSN 2354-1083.

Bài báo số 3 được công bố trên Tạp chí Kết cấu và Công nghệ xây dựng, Hội Kết cấu và Công nghệ Xây dựng Việt Nam, ISSN 1859-3194.

Bài báo số 4 được công bố tại Tuyển tập Công trình khoa học Hội nghị Cơ kỹ thuật và Tự động hóa lần 2 tổ chức tại Trường Đại học Bách khoa Hà Nội ngày 7,8/10/2016, ISBN 978-604-95-0221-7.

Bài báo số 5 công bố trên Tạp chí Khoa học Công nghệ, Trường ĐH Sư phạm Kỹ thuật Hưng Yên, ISSN 2354-0575.

Bài báo số 6 được công bố trên Kỷ yếu Hội nghị Quốc tế RCMME 2014, ISBN 978-604-911-942-2.

CHƯƠNG 1. TỔNG QUAN NGHIÊN CỨU GIẢM DAO ĐỘNG XOẮN VÀ CÁC PHƯƠNG PHÁP XÁC ĐỊNH THAM SỐ TỐI ƯU

1.1. Tổng quan về các nghiên cứu giảm dao động xoắn.

Dao động xoắn của hệ thống quay chủ yếu là do việc truyền tải mô men không đều (mô men thay đổi theo thời gian) giữa các bộ phận quay của máy. Sự dao động xoắn quá mức trong hệ thống cơ học dẫn đến tiếng ồn hoặc phá hủy mỏi. Do đó, chúng cần được ngăn chặn hoặc kiểm soát ngay lập tức để đảm bảo độ tin cậy của hệ thống. Kiểm soát dao động thụ động đã được áp dụng thường xuyên do sự đơn giản của nó trong một miền rộng của mô men xoắn và hiệu quả là chấp nhận được. Trong số các kỹ thuật kiểm soát thụ động, bộ hấp thụ dao động dạng con lắc ly tâm CPVA (centrifugal pendulum vibration absorber) là một trong những phương pháp được sử dụng rộng rãi nhất, có thể tìm thấy trong các máy móc hạng nặng khác nhau, ví dụ máy bay trực thăng và động cơ đốt trong. Các nghiên cứu này đề cập đến việc tối ưu hóa thiết kế của biên dạng rãnh trượt của CPVA để giảm thiểu dao động xoắn trong một hệ thống trục.

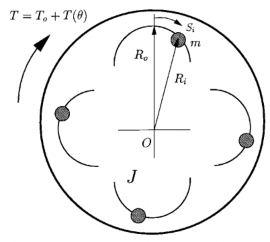
Hình 1.1. Mô hình bộ hấp thụ dao động xoắn CPVAs.

Bộ hấp thụ dao động xoắn CPVA bao gồm khối lượng gắn trên một rotor theo cách để chúng có thể tự do di chuyển theo các đường dẫn quy định liên quan đến các hệ thống quay. Chuyển động của các khối lượng được sử dụng để chống lại các mô men xoắn do đó giảm được dao động xoắn cho các tiết máy quay [54], [65]. Một trong những

thiết kế đầu tiên của về CPVA được giới thiệu và công bố bởi Kutzbach, ở đó cấu tạo của CPVA gồm những khối lượng chuyển động trong các rãnh chữ U chứa đầy chất lỏng (Hình 1.1).

Năm 1929, Carter phát triển một dạng CPVA dùng cho động cơ diesel [25]. Sau đó, CPVA với thiết kế khác nhau đã được giới thiệu để sử dụng cho một phạm vi rộng hơn của các điều kiện hoạt động của hệ thống. Taylor [57] đã đề xuất CPVA để sử dụng trong động cơ máy bay với điều kiện tốc độ thay đổi. Trong nghiên cứu này, trọng lượng của khối lượng ly tâm được thiết kế sao cho lực phục hồi thay đổi theo tốc độ.

Sarazin [53] giới thiệu CPVA, bao gồm một con lắc thiết kế nhỏ gọn với các con lăn áp dụng cho động cơ máy bay. Cho đến đầu năm 1980, phần lớn các thiết kế của CPVAs đã sử dụng các biên dạng tròn [21], [34]. Sau đó, các dạng đường dẫn không tròn khác nhau đã được xem xét cho thiết kế CPVA, chẳng hạn như đường xiclôít [40], epi- xiclôít [26], [38] và các đường đẳng thời (tautochronic curve) [28], [41].

Mayet và Ulbrich [41] trình bày thiết kế theo các đường đẳng thời cho bộ hấp thụ đơn để có được các phương trình trung bình của chuyển động cho trạng thái ổn định. Họ cũng thu được các phương trình tuyến tính và phi tuyến tính và tối ưu cho các CPVA có dạng đường dẫn đẳng thời bằng cách sử dụng công thức Hamilton trung bình [42].

Bên cạnh các nghiên cứu lý thuyết, các nghiên cứu thực nghiệm về CPVA cũng đã được thực hiện.

Shaw và cộng sự [34], [48], [54] đã thí nghiệm hiệu quả của các đặc tính mô men dao động đối với trạng thái ổn định của một hệ thống trục-CPVA thông qua các thí nghiệm. Các nghiên cứu tính toán này chỉ ra rằng các khối lượng chuyển động trong các rãnh trượt tròn có tâm trùng với tâm của trục là tốt nhất, đặc biệt số bộ CPVA sử dụng là số chẵn thì hiệu quả giảm dao động xoắn sẽ là tốt nhất (hình 1.1).

Mayet và các cộng sự [43], [44] tiến hành thí nghiệm thử nghiệm trạng thái ổn định và đáp ứng tức thời của tốc độ góc của hệ thống quay với CPVA.

Ngày nay, các nghiên cứu về CPVA đang gia tăng sự quan tâm do sự gia tăng liên tục nhu cầu về hiệu suất nhiên liệu cao hơn, lượng phát thải thấp hơn, và hoạt động

êm ái của hệ thống quay.

Swank và Lindemann [55] đã đề xuất một sự kết hợp cả hai bộ hấp thụ dạng khối lượng TMD (tuned mass damper) và dạng con lắc ly tâm CPVA sử dụng cho hệ thống truyền động hiện đại.

Gần đây, Sedaghati và các cộng sự [56] đã phát triển một bộ giảm dao động xoắn bằng cách kết hợp CPVA truyền thống và bộ giảm chấn từ.

Nhìn chung, một số lượng lớn các nghiên cứu về dao động xoắn của trục và CPVA đã được tiến hành về tốc độ quay của trục hoặc sự thay đổi gia tốc góc [34], [48], [54]. Các đáp ứng ổn định của dao động xoắn thường được xem xét trong hầu hết các nghiên cứu [34], [40], [41], [42], [43], [44], [48], [54].

Tuy nhiên, dao động xoắn được xác định bởi góc xoắn tương đối giữa hai đầu của trục hiếm khi được thảo luận. Trên thực tế, việc xác định dao động xoắn của trục là rất quan trọng vì nó cho phép xác định ứng suất trong trục, cũng như đánh giá độ bền mỏi của trục [35].

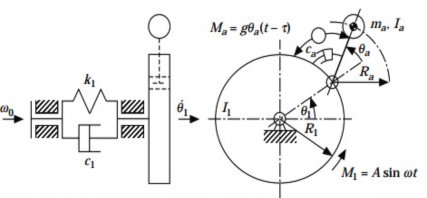
Hình 1.2. Mô hình bộ hấp thụ dao động CDR.

Hosek [35] đề xuất bộ hấp thụ cộng hưởng ly tâm (CDR-centrifugal delayed resonator), đây là thiết bị điều khiển được để giảm dao động xoắn trong các cấu trúc cơ học quay. Trong nghiên cứu này Hosek mô hình hóa trục quay đều với vận tốc góc ω0 gồm ba thành phần: lò xo xoắn có độ cứng xoắn k1, cản môi trường có hệ số cản c1 và một đĩa có mô men quán tính I1. Mô men kích động do hệ thống chấp hành lắp với trục được mô hình dưới dạng tuần hoàn M1=Asin ωt. Ma(t) là mô men điều khiển để bình ổn

dao động xoắn của trục; R1, Ra và θa lần lượt là bán kính trục, chiều dài con lắc và góc quay tương đối của con lắc so với trục.

Phương trình vi phân dao động của cơ hệ:

a a a

I

m R2R R



(t)I

m R2  (t) c  (t)

a a a a a a

m R R 2(t) M

(t)  0

1 1 1 1 1

a 1 a 0 a a

I

n I

n m

R2R R



(t) c 

(t) k  (t) 

a a a a a

n I

n m

R2R R

(t) n c (t) n M

(t) M

(t)  0

a a a a a

a a a a a a a

Trong đó:

θ1 là góc quay của trục;

1 1 0t là góc xoắn giữa hai đầu trục. ma, ca lần

lượt là khối lượng và hệ số cản nhớt của bộ hấp thụ dao động. I1, Ia lần lượt là mô men quán tính khối lượng của trục và CDR. Ma(t) là mô men điều khiển để bình ổn dao động xoắn của trục

Nghiên cứu này cũng tập trung về ổn định và điều khiển dao động, nghiên cứu chưa tập trung cho thiết kế tối ưu của bộ hấp thụ dao động. Các kết quả nghiên cứu mà Hosek đưa ra là:

- Trong trạng thái ổn định, CDR có khả năng loại bỏ hoàn toàn các dao động không mong muốn của cấu trúc chính theo kích động của mô men điều hòa;

- Do điều chỉnh được thời gian thực, CDR hoạt động hoàn toàn với các vấn đề dao động xoắn với thời gian dao động khác nhau. Nó có thể đáp ứng với một dải tần cực kỳ rộng, đặc biệt trong trường hợp tần số nhiễu loạn có xu hướng gia tăng với vận tốc góc của hệ chính;

- Thuật toán điều khiển cho CDR rất đơn giản để thực hiện đặc biệt là sử dụng các thiết bị xử lý tín hiệu số tiên tiến; Do đặc tính thụ động của CDR, nó vẫn có thể hoạt động một phần ngay cả trong trường hợp kiểm soát thất bại khi giả sử rằng con lắc thụ động ly tâm thụ động được sử dụng đúng cách.

Từ các nghiên cứu trên ta thấy rằng các tác giả khi nghiên cứu chỉ tập trung vào nghiên cứu sự ổn định và điều khiển chuyển động của các bộ hấp thụ dao động xoắn, nhưng rất hiếm các nghiên cứu xác định tham số tối ưu của bộ hấp thụ dao động để giảm

dao động xoắn cho trục máy như tỷ số cản nhớt, tỷ số giữa tần số riêng của DVA và trục từ đó cho phép chọn bộ cản nhớt và độ cứng lò xo cho thiết kế DVA tối ưu.

Trong [21], [25], [26], [34], [41] đã nghiên cứu giảm dao động xoắn khi sử dụng các bộ hấp thụ dao động. Tuy nhiên, các nghiên cứu này chỉ xét đến chuyển động của bộ hấp thụ dao động và tập trung nghiên cứu tìm biên dạng rãnh trượt tối ưu của các khối lượng m của bộ hấp thụ và số lượng bộ hấp thụ sử dụng với mục tiêu ổn định dao động xoắn của hệ. Trong các phương trình vi phân dao động của cơ hệ, các nghiên cứu này chưa xét đến dao động xoắn của trục.

Trong các nghiên cứu [35], [44] các tác giả mô hình hóa trục máy bao gồm một lò xo xoắn có độ cứng ks và một đĩa có độ cứng Jr chịu tác dụng của cản môi trường với hệ số cản cs. Để giảm dao động xoắn cho trục các nghiên cứu đề xuất lắp bộ hấp thụ dao động CDR (centrifugal delayed resonator) và DVA. Tuy nhiên các nghiên cứu này chỉ tập trung vào điều khiển dao động để bình ổn dao động xoắn. Nghiên cứu chưa tập trung tìm tham số tối ưu của bộ hấp thụ dao động để giảm dao động xoắn cho trục máy.

Gần đây, trong [7], [9], [10], [14], [30] đã nghiên cứu xác định các tham số tối ưu cho bộ hấp thụ DVA lắp trên trục máy chịu xoắn như các hình 1.3, 1.4 và hình 1.5. Trong các nghiên cứu này các tác giả sử dụng các phương pháp số để xác định tham số tối ưu.



Hình 1.3. Mô hình bộ hấp thụ dao động.

Trong [7], [9] các tác giả tính toán tham số tối ưu giảm dao động xoắn cho trục chính máy tiện vạn năng T616 bằng cách lắp bộ hấp thụ DVA có dạng như hình 1.3. Bộ hấp thụ dao động DVA trong [7], [9] có dạng con lắc lệch tâm được liên kết với rotor của trục chính thông qua bộ cản nhớt c và lò xo xoắn km. Nghiên cứu sử dụng phương

pháp quy hoạch thực nghiệm Taguchi kết hợp mô phỏng số trên Maple. Nghiên cứu đã mô phỏng số dao động xoắn của trục với bộ DVA tối ưu cho đáp ứng tốt so với khi chưa lắp DVA.







Trong nghiên cứu [10] cũng sử dụng phương pháp quy hoạch thực nghiệm Taguchi cho mô hình trục máy chịu xoắn có lắp bộ DVA có dạng con lắc ly tâm (hình 1.4). Nghiên cứu này đã chỉ ra rằng, tuy có đáp ứng tốt về hiệu quả giảm dao động xoắn cho trục, tuy nhiên do bản thân bộ DVA có dạng con lắc ly tâm, lại lắp trên trục máy quay nên gây ra sự mất ổn định cho trục, đặc biệt phản lực động lực tại các khớp nối rất lớn. Nghiên cứu kết luận rằng khi nghiên cứu tính toán tham số tối ưu cho bộ DVA không những chỉ quan tâm đến hiệu quả giảm dao động xoắn mà cần phải xét đến tính ổn định của cơ hệ, đặc biệt quan tâm đến phản lực động lực tại các khớp nối để nâng cao tuổi thọ của các khớp nối, tránh hiện tượng phá hủy khớp.

Hình 1.4. Mô hình bộ hấp thụ dao động dạng con lắc ly tâm.

Trong nghiên cứu [14] sử dụng phương pháp hồi quy phi tuyến Levenberg- Marquadt để xây dựng hàm hồi quy phi tuyến mô tả quan hệ giữa các thông số của bộ hấp thụ DVA dạng rãnh trượt tròn (hình 1.5), bao gồm tỷ số khối lượng, tỷ số độ cứng và tỷ số cản nhớt.

Nghiên cứu đã thiết lập được hàm hồi quy phi tuyến mô tả quan hệ giữa các thông số DVA và dao động xoắn của trục; đánh giá độ tin cậy của hàm hồi quy thông qua đánh giá phương sai. Từ đó, xác định được tham số tối ưu của DVA nhằm giảm dao động xoắn cho trục.