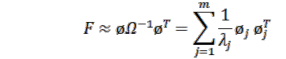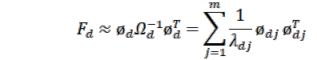đơn bằng cách đưa ra chỉ số hư hỏng để định lượng hư hỏng. Kết quả chứng minh rằng phương pháp để xuất giảm được thời gian tính toán và xác định chính xác khu vực hư hỏng.
2.2.2.4. Phương pháp dựa trên ma trận độ mềm
Trong thập kỷ qua, các nhà nghiên cứu đã phát hiện ra rằng ma trận độ mềm dao động riêng có thể là một tham số nhạy cảm hơn so với tần số riêng hoặc hình dạng dao động đơn lẻ để phát hiện hư hỏng trong kết cấu [115]. Pandey và cộng sự [116] đã đề xuất một phương pháp phát hiện hư hỏng dựa trên sự khác biệt giữa các ma trận độ mềm của kết cấu bị hư hỏng và kết cấu chưa hư hỏng. Ma trận độ mềm của kết cấu không bị hư hỏng được xác định bằng công thức:
(2.29) |
Có thể bạn quan tâm!
-
 Tổng Quan Về Giám Sát Sức Khỏe Kết Cấu Công Trình Dựa Trên Phương Pháp Đo Nhận Dạng Dao Động
Tổng Quan Về Giám Sát Sức Khỏe Kết Cấu Công Trình Dựa Trên Phương Pháp Đo Nhận Dạng Dao Động -
 Tình Hình Nghiên Cứu Ở Việt Nam Về Giám Sát Sức Khỏe Kết Cấu Công Trình Dựa Trên Phương Pháp Đo Nhận Dạng Dao Động
Tình Hình Nghiên Cứu Ở Việt Nam Về Giám Sát Sức Khỏe Kết Cấu Công Trình Dựa Trên Phương Pháp Đo Nhận Dạng Dao Động -
 Phương Pháp Dựa Vào Sự Thay Đổi Của Hình Dạng Dao Động
Phương Pháp Dựa Vào Sự Thay Đổi Của Hình Dạng Dao Động -
 Chẩn Đoán Hư Hỏng Kết Cấu Dựa Trên Kết Quả Đo Nhận Dạng Dao Động Sử Dụng Mạng Nơ Ron Nhân Tạo.
Chẩn Đoán Hư Hỏng Kết Cấu Dựa Trên Kết Quả Đo Nhận Dạng Dao Động Sử Dụng Mạng Nơ Ron Nhân Tạo. -
 Áp Dụng Pso Kết Hợp Với Ann Để Chẩn Đoán Các Hư Hỏng Cho Mô Hình Số
Áp Dụng Pso Kết Hợp Với Ann Để Chẩn Đoán Các Hư Hỏng Cho Mô Hình Số -
 Các Chỉ Số Đánh Giá Hiệu Suất Của Các Thuật Toán - Kịch Bản Hư Hỏng Đơn
Các Chỉ Số Đánh Giá Hiệu Suất Của Các Thuật Toán - Kịch Bản Hư Hỏng Đơn
Xem toàn bộ 154 trang tài liệu này.
Trong đó ![]() là ma trận dao động riêng của các hình dạng dao động chuẩn hóa khối lượng
là ma trận dao động riêng của các hình dạng dao động chuẩn hóa khối lượng ![]() và m là số lượng hình dạng dao động đo được. Theo cách tương tự, ma trận độ mềm của kết cấu bị hư hỏng được xác định từ công thức 2.30:
và m là số lượng hình dạng dao động đo được. Theo cách tương tự, ma trận độ mềm của kết cấu bị hư hỏng được xác định từ công thức 2.30:
(2.30) |
Sự khác biệt giữa các ma trận độ mềm của các kết cấu bị hư hỏng và không bị hư hỏng được xác định từ công thức 2.31
(2.31) |
Chỉ có một vài dao động đầu tiên của kết cấu là cần thiết cho việc xây dựng ma trận độ mềm. Việc tổng hợp ma trận độ mềm hoàn chỉnh sẽ yêu cầu đo tất cả các hình dạng và tần số của dao động. Thông thường, hư hỏng được phát hiện dựa trên ma trận độ mềm, bằng cách so sánh ma trận độ mềm được tổng hợp sử dụng các dao động của kết cấu đã hư hỏng với ma trận độ mềm được tổng hợp bằng các dao động của kết cấu chưa bị hư hỏng hoặc ma trận độ mềm từ mô hình số. Bình phương của tần số dao động riêng và ma trận độ mềm đo được có mối quan hệ nghịch đảo, do đó phương pháp này nhạy cảm nhất với sự thay đổi của các dao động trong dải tần số thấp hơn.
Ma trận độ mềm có tốc độ hội tụ nhanh với các giá trị tần số tăng dần, đó là một lợi thế của việc sử dụng tính linh hoạt thay vì độ cứng [89]. Reich và cộng sự [117] đã đề xuất một phương pháp xác định các hư hỏng trong kết cấu dựa trên những thay đổi
tương đối trong các thuộc tính linh hoạt cục bộ. Một quy trình phân rã thành ma trận độ mềm toàn cục được xác định bằng thực nghiệm hoặc các tín hiệu đầu ra của thực nghiệm dao động đã được áp dụng để thu được ma trận độ mềm. Lý thuyết này dựa trên việc phân vùng chức năng năng lượng của một hệ động lực rời rạc, trong đó hệ số nhân Lagrange được sử dụng để ràng buộc tương thích giữa các vùng kết cấu lân cận. Hiệu quả của phương pháp đề xuất đã được tiến hành để phát hiện hư hỏng của mô hình trụ cầu thực tế.
Bernal [118] đã trình bày kỹ thuật để xác định vị trí hư hỏng trong các kết cấu có thể được coi là tuyến tính ở trạng thái trước và sau hư hỏng. Phương pháp xác định vị trí hư hỏng của vectơ được sử dụng để xác định vị trí hư hỏng trong kết cấu. Trong nghiên cứu này, ma trận khối lượng được xem là ma trận đường chéo và không cần xây dựng mô hình tham chiếu của kết cấu. Từ mô hình số được xây dựng, các trường hợp hư hỏng đơn lẻ cũng như hư hỏng tại nhiều vị trí đã được xác định chính xác. Trong đó ảnh hưởng của nhiễu được đánh giá.
Patjawit và cộng sự [119] đã trình bày một phương pháp theo dòi các hư hỏng xảy ra trong kết cấu cầu. Chỉ số linh hoạt toàn cục đã được đề xuất để xác định các hư hỏng của cầu nằm trên đường cao tốc. Chỉ số được xây dựng bằng cách sử dụng định mức phổ của ma trận độ mềm, thu được từ các điểm tham chiếu được chọn, trong đó các tham số này rấy nhạy cảm với biến dạng của kết cấu. Ma trận độ mềm được đánh giá từ các phản ứng động tại các điểm tham chiếu này dưới tác động của dao động cưỡng bức. Một nghiên cứu trong phòng thí nghiệm đã được thực hiện bằng cách sử dụng một dầm thép giản đơn và một dầm bê tông cốt thép để đánh giá hiệu quả của phương pháp đề xuất. Kết quả chỉ ra rằng sự thay đổi trong giá trị chỉ số linh hoạt toàn cục đủ nhạy cảm với những hư hỏng gây ra bởi sự xuống cấp của kết cấu.
Choi và cộng sự [120] đã phát triển một phương pháp để xác định và đánh giá hư hỏng cục bộ trong dầm gỗ, sử dụng hai thuật toán tối ưu. Một chỉ số hư hỏng mới được giới thiệu bằng cách kết hợp chỉ số hư hỏng và phương pháp linh hoạt. Đánh giá phân tích đã được thực hiện để so sánh và xác minh khả năng của các thuật toán xác định vị trí hư hỏng truyền thống và đề xuất trong việc xác định vị trí hư hỏng đơn và hư hỏng tại nhiều phần tử trong dầm gỗ. Các nghiên cứu trong phòng thí nghiệm cũng được thực hiện để đánh giá tính hiệu quả của các phương pháp đề xuất. Kết quả cho thấy
phương pháp này có khả năng xác định đồng thời vị trí hư hỏng cho tối đa tại bốn vị trí cho kết cấu dầm giản đơn.
Ưu điểm của phương pháp dựa vào sự thay đổi của hình dạng dao động là thay đổi về hình dạng dao động thường nhạy hơn nhiều so với hư hỏng cục bộ khi so sánh với thay đổi về tần số riêng và hệ số cản. Nhược điểm của phương pháp này là rất khó để thu được hình dạng dao động và có thể cần một số lượng lớn các vị trí đo để mô tả chính xác các véc tơ chỉ phương và cung cấp đủ dữ liệu để xác định vị trí hư hỏng.
2.2.3. Phương pháp dựa trên hàm đáp ứng tần số
Các phương pháp dựa trên hàm đáp ứng tần số (FRF - Frequency response function) có những lợi thế nhất định so với dữ liệu phân tích từ các mode dao động để xác định hư hỏng [121]. Một trong những phương pháp xác định hư hỏng dựa trên hàm đáp ứng tần số là phương pháp dựa trên đường cong hàm đáp ứng tần số. Về cơ bản, phương pháp này là một phần mở rộng của phương pháp mà Pandey, Biswas and Samman [102] đã đề xuất. Phương pháp có thể áp dụng cho tất cả các tần số trong phạm vi đo. Cụ thể, phương pháp này sử dụng dữ liệu hàm đáp ứng tần số thay vì chỉ sử dụng dữ liệu hình dạng dao động.
Đường cong của mỗi tần số được xác định theo công thức 2.32:
(2.32) |
Trong đó hàm đáp ứng tần số được đo tại vị trí ![]() cho vị trí đặt lực tại
cho vị trí đặt lực tại ![]() . Sự khác biệt tuyệt đối giữa đường cong hàm đáp ứng tần số của kết cấu bị hư hỏng và không bị hư hỏng tại vị trí
. Sự khác biệt tuyệt đối giữa đường cong hàm đáp ứng tần số của kết cấu bị hư hỏng và không bị hư hỏng tại vị trí ![]() , dọc theo dải tần số đã chọn, được tính cho một lực tác dụng tại điểm
, dọc theo dải tần số đã chọn, được tính cho một lực tác dụng tại điểm ![]() như phương trình 2.33 và 2.34.
như phương trình 2.33 và 2.34.
(2.33) | |
| (2.34) |
![]()
![]()
![]()
Các nghiên cứu thực nghiệm để xác định ảnh hưởng của vết nứt và hư hỏng đối với các kết cấu được thực hiện bởi Owolabi và cộng sự [122]. Những thay đổi trong ba tần số dao động riêng đầu tiên và biên độ tương ứng của các gia tốc đo được là các tham số để xác định hư hỏng. Nghiên cứu thực nghiệm đã được thực hiện cho hai bộ dầm làm bằng nhôm, mỗi bộ bao gồm bảy dầm giản đơn. Các vết nứt được bố trí tại bảy vị trí khác nhau và tỷ lệ độ sâu vết nứt dao động từ 0,1 đến 0,7 ( là chiều dày
của dầm). Các hàm đáp ứng tần số gia tốc được đo tại bảy điểm khác nhau trên mỗi mô hình của dầm. Từ kết quả thí nghiệm, người ta thấy rằng tần số cơ bản cho thấy xu hướng giảm rò ràng khi tỷ lệ độ sâu vết nứt tăng lên. Biên độ của FRF cũng cho thấy xu hướng giảm khi vết nứt ngày càng lớn.
Liszkai [123] đã giải quyết vấn đề phát hiện hư hỏng kết cấu bằng cách sử dụng thông tin dao động tuyến tính có trong các hàm đáp ứng tần số. Hai loại thuật toán GA đã được thực hiện để giải quyết vấn đề tối ưu hóa trong bài toán phát hiện hư hỏng kết cấu. Các thuật toán đề xuất được đánh giá trên các mô hình số mô phỏng các loại kết cấu khác nhau với độ phức tạp tăng dần. Trong nghiên cứu này, độ chính xác phát hiện hư hỏng dưới ảnh hưởng của nhiễu đã được nghiên cứu. Kết quả nghiên cứu cho thấy phương pháp xác định hư hỏng được đề xuất đem lại kết quả chính xác, ngay cả trong trường hợp độ nhiễu lớn.
Hwang và cộng sự [124] đã trình bày các phương pháp để xác định vị trí và mức độ của hư hỏng trong các kết cấu sử dụng dữ liệu hàm đáp ứng tần số (Fast Response Transform - FRF). Phương pháp này đã được kiểm chứng bằng các mô hình số với một dầm hẫng và một cánh quạt máy bay trực thăng. Kết quả chỉ ra rằng phương pháp đề xuất đã xác định chính xác vị trí hư hỏng trong các vật thể xem xét. Dincal [125] đã nghiên cứu hiệu suất của phương pháp mới để xác định hư hỏng kết cấu với điều kiện chỉ có thể sử dụng thông tin đo đạc thực nghiệm để tính toán các hàm đáp ứng tần số. Chương trình được đề xuất, đã sử dụng một thuật toán GA tiên tiến để xác định vị trí hư hỏng và mức độ hư hỏng bằng cách sử dụng các hàm đáp ứng tần số như là các tín hiệu phản hồi. Kết quả nghiên cứu chỉ ra rằng phương pháp đề xuất có thể phát hiện chính xác hư hỏng kết cấu đối với các phần tử bị hư hỏng riêng lẻ hoặc trong một sàn bị hư hỏng, tuy nhiên một vài lỗi nhỏ cũng xảy ra (một số vị trí hư hỏng đã không được xác định chính xác). Từ việc so sánh hiệu suất của phương pháp được đề xuất và các thuật toán truyền thống thường dùng để phát hiện hư hỏng khác nhau đã chứng minh rằng phương pháp đề xuất rất dễ sử dụng, trực quan và chính xác.
Tang [126] xác định hư hỏng kết cấu bằng cách sử dụng tín hiệu đáp ứng tần số và phân tích thành phần chính. Mục tiêu chính của nghiên cứu là phát triển một phương pháp để giải quyết với sự bất định và nhiễu không thể tránh khỏi trong các tình huống thực tế. Một phương pháp trích xuất/khử nhiễu dựa trên phân tích thành phần chính đã được trình bày. Một loạt các phân tích số được thực hiện để kiểm chứng độ
nhạy và tính hiệu quả của phương pháp đề xuất. Tuy nhiên, phương pháp này đã không được kiểm chứng từ các kết quả thí nghiệm. Furukawa và cộng sự [127] đã trình bày phương pháp phát hiện hư hỏng trong kết cấu bằng cách sử dụng các hàm đáp ứng tần số không chắc chắn. Thực nghiệm giả thuyết dựa trên phương pháp tự khởi động đã được giới thiệu để khắc phục các sai số do nhiễu gây ra. Để kiểm tra phương pháp đề xuất, các mô phỏng số sử dụng kết cấu khung hai chiều đã được sử dụng. Kết quả cho thấy rằng phương pháp được đề xuất đã cải thiện độ chính xác nhận dạng trong trường hợp ảnh hưởng của nhiễu lớn.
Link và cộng sự [128] đã phát triển một quy trình phát hiện hư hỏng, sử dụng trực tiếp hàm đáp ứng tần số. Dữ liệu hàm đáp ứng tần số từ kết cấu xảy ra hư hỏng và mô hình phần tử hữu hạn của kết cấu khỏe mạnh đã được sử dụng để tạo ra các hư hỏng khác. Hư hỏng này có thể được tính toán khi các phép đo không đầy đủ có xem xét đến ảnh hưởng của nhiễu đối với kết quả tần số thu được. Kỹ thuật được phát triển trong nghiên cứu này, có thể được sử dụng với các trường hợp dữ liệu đầu vào bất định. Các hư hỏng được xác định là phần trăm giảm độ cứng của các phần tử, do đó chỉ các hư hỏng ảnh hưởng đến tính chất độ cứng của kết cấu được xem xét trong nghiên cứu này. Nghiên cứu mô phỏng được thực hiện với kết cấu dàn trong dải tần số 0 - 512 Hz. Kết quả cho thấy phương pháp được đề xuất có thể xác định nhiều trường hợp hư hỏng và có xét đến ảnh hưởng của nhiễu.
Dackermann và cộng sự [129] đã đề xuất một phương pháp mới để xác định mức độ của hư hỏng trong kết cấu khung hai tầng. Phương pháp đề xuất sử dụng ANN, hàm đáp ứng tần số và để giảm kích thước dữ liệu hàm đáp ứng tần số đo được, kỹ thuật phân tích thành phần chính được áp dụng. Phương pháp được kiểm chứng thông qua thí nghiệm mẫu trong phòng thí nghiệm và mô hình số. Kết quả phát hiện hư hỏng chính xác cho tất cả các dữ liệu với ảnh hưởng của nhiễu bé hơn 10%. Tuy nhiên, phương pháp đề xuất không được tiến hành với nhiều kịch bản hư hỏng khác nhau và kết cấu không gian.
Nozarian và cộng sự [130] đã trình bày một kỹ thuật xác định hư hỏng xảy ra trong các phần tử bằng cách sử dụng hàm đáp ứng tần số của các kết cấu. Những thay đổi của hàm đáp ứng tần số của kết cấu do hư hỏng được đánh giá bằng tần số dao động riêng đo được và thay đổi hình dạng dao động. Phương trình sử dụng để phát hiện hư hỏng trong kết cấu đã được giải quyết bằng phương pháp bình phương nhỏ
nhất để đạt được những thay đổi của các tham số kết cấu. Phương pháp được xác thực bằng các ví dụ số có xét đến ảnh hưởng của nhiễu để chứng minh rằng phương pháp được đề xuất có thể thay thế cho các phương pháp phát hiện hư hỏng thông thường. Phương pháp chỉ ra rằng trong hầu hết các trường hợp hư hỏng, kết quả dự đoán sẽ có độ chính xác cao hơn nếu kết cấu được kích thích với dải tần số cao hơn.
Liu và cộng sự [131] đã đề xuất một sơ đồ sử dụng các hình dạng hàm đáp ứng tần số để xác định khu vực hư hỏng trong kết cấu. Các tham số trong sơ đồ này bao gồm một số sửa đổi quan trọng, như sử dụng các phần ảo của hình dạng hàm đáp ứng tần số và chẩn hóa hình dạng hàm đáp ứng tần số trước khi so sánh. Các phương pháp đề xuất đã cho thấy tiềm năng lớn trong việc xác định khu vực hư hỏng trong kết cấu.
Mặc dù các phương pháp dựa trên hình dạng hàm đáp ứng tần số được đề xuất đã cho thấy những hứa hẹn trong xác định khu vực hư hỏng trong kết cấu, nhưng các bất thường nhỏ do hư hỏng gây ra phải được đưa vào các hình dạng hàm đáp ứng tần số đo được để xác định chính xác hư hỏng.
Ưu điểm của phương pháp dựa trên hàm phản ứng tần số là khả năng thực hiện với giá thành thấp và có thể cung cấp thông tin chi tiết hơn về tình trạng tổng thể của hệ thống. Nhược điểm của phương pháp là cung cấp ít thông tin về khu vực hư hỏng cục bộ trừ khi sử dụng số lượng lớn cảm biến.
2.3. Chẩn đoán hư hỏng kết cấu dựa trên kết quả đo nhận dạng dao động sử dụng thuật toán bầy đàn PSO
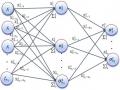
Năm 1995, Kennedy và cộng sự [132-133] phát triển PSO dựa trên tối ưu hóa ngẫu nhiên, lấy cảm hứng từ hành vi xã hội của một đàn chim, đàn cá, một đàn ong và thậm chí đôi khi là hành vi xã hội của con người. Mặc dù PSO là tương tự như thuật toán GA về mặt khởi tạo các phần tử với các giải pháp ngẫu nhiên và tìm kiếm tối ưu toàn cục trong các thế hệ kế tiếp nhưng PSO không trải qua quá trình trao đổi và đột biến, trong khi các phần tử di chuyển phụ thuộc vào các phần tử tại thế hệ trước. Mỗi phần tử di chuyển trong không gian tìm kiếm dựa trên kết quả tối ưu cục bộ hoặc tối ưu toàn cục thu được. Vị trí mỗi phần tử qua mỗi bước lặp được cập nhật như sau:
(2.35) |
![]()
Trong đó là ![]() vị trí của phần tử tại bước lặp thứ
vị trí của phần tử tại bước lặp thứ ![]() và
và ![]() , tương ứng. Trong đề tài này
, tương ứng. Trong đề tài này ![]() là tần số dao động riêng của các mode dao động;
là tần số dao động riêng của các mode dao động; ![]() là vận tốc của phần tử tại bước lặp thứ .
là vận tốc của phần tử tại bước lặp thứ .
Mỗi phần tử ![]() có vị trí tối ưu của riêng nó được hiển thị là
có vị trí tối ưu của riêng nó được hiển thị là ![]() trong đó
trong đó ![]() là số lần lặp. Tối ưu toàn cục trong các lần lặp là
là số lần lặp. Tối ưu toàn cục trong các lần lặp là ![]() , vị trí tối ưu được tìm thấy bởi bất kỳ phần tử nào. Vận tốc phần tử bao gồm ba phần: (1) vận tốc trước, (2) chuyển động theo hướng
, vị trí tối ưu được tìm thấy bởi bất kỳ phần tử nào. Vận tốc phần tử bao gồm ba phần: (1) vận tốc trước, (2) chuyển động theo hướng ![]() và (3) chuyển động theo hướng
và (3) chuyển động theo hướng ![]() . Vận tốc của các phần tử được cập nhật như sau:
. Vận tốc của các phần tử được cập nhật như sau:
(2.36) |
Trong đó ![]() và
và ![]() là các giá trị ngẫu nhiên có giá trị nằm trong khoảng [0, 1];
là các giá trị ngẫu nhiên có giá trị nằm trong khoảng [0, 1]; ![]() và
và ![]() lần lượt là các tham số học tập liên quan đến tối ưu cục bộ và tối ưu toàn cục;
lần lượt là các tham số học tập liên quan đến tối ưu cục bộ và tối ưu toàn cục; ![]() là tham số trọng lượng. Về cơ bản, cứ sau mỗi lần lặp, vận tốc của từng phần tử cũng được gọi là giải pháp tiềm năng, thay đổi giữa các vị trí tối ưu
là tham số trọng lượng. Về cơ bản, cứ sau mỗi lần lặp, vận tốc của từng phần tử cũng được gọi là giải pháp tiềm năng, thay đổi giữa các vị trí tối ưu ![]() ) và tối ưu toàn cục
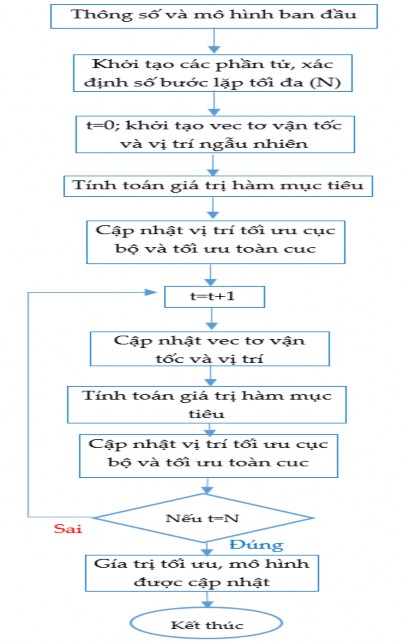
) và tối ưu toàn cục ![]() ). Về mặt toán học, một loạt các phần tử được khởi tạo ngẫu nhiên trong không gian tìm kiếm và di chuyển qua không gian để tìm kiếm các giải pháp mới. Giá trị cuối cùng sẽ là giá trị tối ưu thu được trong quá trình tìm kiếm. Quá trình sử dụng thuật toán PSO để giải quyết các bài toán tối ưu được biển diễn như sơ đồ hình 2.1:
). Về mặt toán học, một loạt các phần tử được khởi tạo ngẫu nhiên trong không gian tìm kiếm và di chuyển qua không gian để tìm kiếm các giải pháp mới. Giá trị cuối cùng sẽ là giá trị tối ưu thu được trong quá trình tìm kiếm. Quá trình sử dụng thuật toán PSO để giải quyết các bài toán tối ưu được biển diễn như sơ đồ hình 2.1:
Hình 2.1. Sơ đồ thuật toán tối ưu hoá bầy đàn – PSO |
Ưu điểm: Trong PSO, với khả năng tìm kiếm trong không gian rộng lớn, có thể giữ lại tất cả các thông tin của các phần tử mà nó đã sử dụng. Từ đó thông tin của tất các các phần tử qua các lần lặp sẽ được lưu giữ và các phần tử với giải pháp tốt hơn sẽ được lựa chọn.
Nhược điểm: Trong PSO không có toán tử lựa chọn, biến đổi để cải thiện được chất lượng của thế hệ sau, dẫn đến giảm hiệu quả của kết quả tìm kiếm tối ưu. Ngoài ra quá trình tìm kiếm ngẫu nhiên của PSO thường tốn thời gian, sẽ khó áp dụng cho các vấn đề thực tế với kết cấu quy mô lớn, độ phức tạp cao.