Mô Hình Bộ Hấp Thụ Dao Động Dạng Con Rãnh Trượt Tròn.

k

(t)

s

(t) (t)

(t)

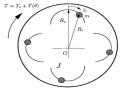
Hình 1.5. Mô hình bộ hấp thụ dao động dạng con rãnh trượt tròn.

Từ các nghiên cứu [7], [9], [10], [14], [30] ta nhận thấy rằng:

So với mô hình bộ hấp thụ dao động trong các nghiên cứu [21], [28], [34], [38], [41], [42], [43], [44] mô hình bộ hấp thụ trong các nghiên cứu này đều có dạng lệch tâm, trục máy dao động không ổn định, phản lực động lực tại các khớp nối rất lớn và có thể phá hủy các khớp nối.

Phương pháp sử dụng trong các nghiên cứu này là phương pháp số chẳng hạn phương pháp quy hoạch thực nghiệm Taguchi, phương pháp hồi quy phi tuyến, … do đó chỉ có thể áp dụng cho các trục máy có số liệu cụ thể mà không thể áp dụng cho trục có số liệu khác nhau, tổng quát. Tuy nhiên, nếu xét về hiệu quả giảm dao động xoắn thì việc lắp các bộ hấp thụ dao động này rõ ràng mang lại hiệu quả tốt so với khi chưa lắp.

Có thể bạn quan tâm!

• Nghiên cứu giảm dao động xoắn của trục máy bằng bộ hấp thụ dao động - 1
• Nghiên cứu giảm dao động xoắn của trục máy bằng bộ hấp thụ dao động - 2
• Tổng Quan Nghiên Cứu Giảm Dao Động Xoắn Và Các Phương Pháp Xác Định Tham Số Tối Ưu
• Một Số Bộ Thông Số Tối Ưu Của Bộ Hấp Thụ Dao Động Thụ Động Cho Hệ Một Bậc Tự Do Không Cản Chịu Kích Động Ồn Trắng.
• Tính Bộ Hấp Thụ Dao Động Thụ Động Cho Hệ Chính Có Cản Nhớt.
• Tính Toán Tham Số Tối Ưu Trong Trường Hợp Hệ Chính Có Nhiều Bậc Tự Do

Xem toàn bộ 153 trang tài liệu này.

1.2. Tổng quan về bộ hấp thụ dao động DVA và các phương pháp tính toán giảm dao động.

Như đã phân tích ở trên các nghiên cứu về dao động xoắn chủ yếu tập trung vào đáp ứng ổn định và điều khiển dao động xoắn. Dao động xoắn được xác định bởi góc xoắn tương đối giữa hai đầu của trục hiếm khi được thảo luận. Trên thực tế, việc xác định dao động xoắn của trục là rất quan trọng vì nó cho phép xác định ứng suất trong trục, cũng như đánh giá độ bền mỏi của trục [35].

Hosek [35] mô hình hóa trục gồm ba thành phần: lò xo xoắn có độ cứng xoắn k1, cản môi trường có hệ số cản c1 và một đĩa có mô men quán tính I1. Để giảm dao động xoắn cho trục máy, Hosek đề xuất lắp bộ hấp thụ cộng hưởng ly tâm CDR, đây là thiết bị điều khiển được để giảm dao động xoắn trong các cấu trúc cơ học quay. Tuy nhiên

nghiên cứu này tập trung vào bài toán ổn định và điều khiển dao động, nghiên cứu không tập trung vào tìm tham số tối ưu của bộ hấp thụ dao động.

Trong [59], [60] các tác giả đề xuất lắp bộ hấp thụ dao động DVA dạng đĩa – lò xo – cản nhớt (thực chất là một dạng riêng của CPVA [40], [43], [44]) và tính toán xác định tham số tối ưu của bộ DVA bằng phương pháp giải tích.

Phần sau đây trình bày về tổng quan bộ hấp thụ động lực DVA: tổng quan về lịch sử hình thành và phát triển, các nghiên cứu về DVA, nguyên lý của bộ hấp thụ dao động DVA, các phương pháp tính toán giải tích cho bộ hấp thụ DVA và các tiêu chuẩn tính toán.

1.2.1 Giới thiệu chung.

Trong phương pháp hấp thụ thụ động, bộ hấp thụ dao động thụ động được gắn thêm vào hệ máy hay kết cấu. Mục đích của việc sử dụng bộ hấp thụ dao động thụ động là để hấp thụ một phần năng lượng của hệ chính. Ưu điểm của phương pháp là không cần năng lượng sinh ra bởi bộ tạo nguồn lực nên đơn giản cho công tác duy tu, bảo dưỡng.

(TMD)

k1

F1

m

x1

F2 c1

M

x2

k2 c2

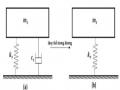
Hình 1.6. Bộ hấp thụ dao động và hệ chính.

Sự hấp thụ được thực hiện bằng cách truyền một phần năng lượng dao động có hại từ hệ chính tới bộ hấp thụ dao động thụ động. Bộ hấp thụ dao động thụ động dạng khối lượng gọi tắt là TMD có thể mô tả như là một khối lượng được gắn với hệ chính thông qua lò xo và giảm chấn dạng cản nhớt. Sơ đồ kết nối giữa bộ hấp thụ dao động thụ động và hệ dao động chính được biểu diễn trên hình 1.6.

Việc ứng dụng bộ hấp thụ dao động thụ động được nghiên cứu lần đầu tiên bởi Frahm vào năm 1909 [31]. Trong đó bộ hấp thụ dao động thụ động có khối lượng m và

lò so với độ cứng k1. Hệ chính là vật M được gắn với nền bằng lò so có độ cứng k2. Khi cả hai hệ đều không chứa lực cản, dưới tác dụng của kích động điều hòa, hệ dao động chính M có thể đứng yên không chuyển động nếu tần số riêng của bộ hấp thụ dao động

k1 m





thụ động, a , được chọn bằng tần số của lực kích động.

Lý thuyết về bộ hấp thụ dao động thụ động có cản nhớt được Den Hartog [29] phát triển cho các trường hợp hệ chính có cản nhớt. Ông đã đưa ra phương pháp tính toán thông số tối ưu của bộ hấp thụ dao động thụ động. Sau đó, việc nghiên cứu bộ hấp thụ dao động thụ động cho các hệ chính có cản nhớt được tiếp tục bởi Bishop và Welbourn [23]. Trong nhiều trường hợp, việc xác định các thông số tối ưu dưới dạng giải tích cho bộ hấp thụ dao động thụ động đối với các hệ có cản nhớt là không thể thực hiện được. Do vậy phương pháp số đã được nhiều tác giả nghiên cứu để giải quyết các bài toán này:

- Jennige và Frohrib (1977) đã dùng phương pháp số để đánh giá bộ hấp thụ dao động thụ động dạng quay cho những cơ hệ chịu uốn và xoắn.

- Ioi và Ikeda (1978), [36] đưa ra các công thức kinh nghiệm để tính toán các thông số tối ưu của bộ hấp thụ dao động thụ động cho những hệ chính có hệ số cản nhớt nhỏ.

- Randall et al. (1981) đã đưa ra các đồ thị phụ thuộc theo tham số cho các thông số tối ưu khi hệ chính có cản nhớt.

- Warbuton và Ayorinde (1981), [67] cũng đưa ra phương pháp tính các thông số tối ưu của bộ hấp thụ dao động thụ động để giảm biên độ dao động cho hệ chính với một số thông số cho trước.

1.2.2 Nguyên lý cơ bản của bộ hấp thụ dao động thụ động.

Hình 1.6 mô tả hệ dao động một bậc tự do có khối lượng M chịu kích động bởi lực F2(t). Để giảm đáp ứng dao động của hệ chính ta gắn vào hệ dao động một bộ hấp thụ dao động thụ động khối lượng m.

Phương trình chuyển động của cơ hệ được mô tả bởi:

MX(t) CX(t) KX(t) F(t)

(1.1)

cứng:

Ở đây X(t) là véctơ dịch chuyển tương đối của các vật so với nền.

M, C, K tương ứng là các ma trận khối lượng, ma trận cản nhớt và ma trận độ

X(t) x2 (t), F(t) F2 (t)

x (t) F (t)

1 1 

M M

0 C c1 c2

c1 

K k1 k2

k1 

0 m,

c c ,

k k 

(1.2)



1 1 

1 1 

Nhân

x 2

vào hai vế của phương trình (1.1) và lấy trung bình, ta có:

M

x x

c

c 

x2

k

k 

x x

 F (t)x

c x x

k x x

2 2 2 1 2 2 1 2 2 2 2 1 1 2 1 1 2



(1.3)

1 2 1 2 1 1 2 1 2 2 1 1 2 1 2

m x x c x2c x x k x x k x x F (t)x

ở đây <…> là kỳ vọng toán học cho trường hợp hệ chịu kích động ngẫu nhiên hay giá trị trung bình cho trường hợp kích động điều hoà.

Từ x2(t)x2(t)  0 , x2(t)x2(t)  0

và cộng 2 phương trình trên lại, ta có

phương trình cân bằng năng lượng đơn giản:

c x2F (t) F (t)x

m

x x (1.4)

2 2 2 1 2 1 2

trong đó,

-c2

x 2 là năng lượng tiêu hao do tác dụng của lực cản.

2

- F (t) F (t)x

là năng lượng do kích động từ bên ngoài

2 1 2

- Phần năng lượng bằng [ mx1x2] được truyền từ hệ chính sang khối lượng lắp thêm m.

Đó chính là nguyên lý hoạt động của bộ hấp thụ dao động thụ động. Trong trường hợp dấu của [ m x1x 2] dương, bộ hấp thụ dao động thụ động đã hấp thụ một phần năng lượng của dao động. Nếu năng lượng truyền từ hệ chính sang bộ hấp thụ dao động thụ động càng lớn thì dao động của hệ chính sẽ càng nhỏ.

Trường hợp dấu của [ m x1x2] âm, lúc này hệ phụ sẽ truyền năng lượng cho hệ chính, hệ chính sẽ dao động mạnh thêm. Như vậy trong quá trình dao động luôn có

sự trao đổi năng lượng giữa hệ chính và hệ phụ. Bộ hấp thụ dao động thụ động sẽ đạt hiệu quả tốt khi dao động của bộ hấp thụ lệch pha 90o so với dao động của hệ chính. Lúc này, gia tốc của bộ hấp thụ dao động thụ động cùng chiều với vận tốc của hệ chính. Khi bộ hấp thụ dao động làm việc có hiệu quả, nó làm tăng hệ số cản của hệ chính theo công thức (1.5)

c2eq

c2

m x1x 2

2

x 2 

(1.5)

Tương tù nhân x2 vào hai vế của phương trình (1.1) và lấy trung bình, ta có:

M

x x

c

c 

x x

k

k x2

 F (t)x

c x x

k x x

2 2 2 1 2 2 2 1 2 2 2 1 1 2 1 1 2



(1.6)

1 2 1 2 2 1 1 2 1 2 1 1 2 1 2

m x x c x x c x x k x2k x x F (t)x

Từ x2(t)x2(t)  0 , x2(t)x2(t)  0

và cộng 2 phương trình trên lại, ta có

phương trình :

m x x k x2 F (t) F (t)x M x x

(1.7)

1 2 2 2 2 1 2 2 2

x1 x2

x2

2

Vậy độ cứng tương đương của hệ chính được xác định theo công thức:

k2 eq

k 2 m

(1.8)

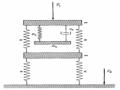
Ta có thể sử dụng hình 1.7 thay cho hình 1.1 với k2eq và c2eq là độ cứng và hệ số cản của hệ chính tương đương.

F1+ F2

M+m

k2eq

c2eq

x2

Hình 1.7. Sơ đồ của hệ chính tương đương.

1.2.3. Tính bộ hấp thụ dao động thụ động cho hệ chính không có cản nhớt.

Hình 1.8 mô tả hệ dao động một bậc tự do có khối lượng M chịu kích động bởi lực F(t). Để giảm đáp ứng dao động của hệ chính ta gắn vào hệ dao động một bộ hấp thụ dao động thụ động TMD có khối lượng m.

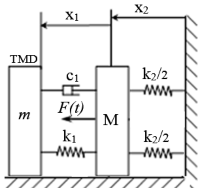
Hình 1.8. Mô hình hệ chính không cản có lắp bộ TMD.

Phương trình vi phân chuyển động của cơ hệ được xác định theo phương trình Lagrăng II :

M mx2mx1k2x2F (t)

mx mx c x k x  0

(1.9a)

1 2 1 1 1 1

Phương pháp hai điểm cố định.

Việc sử dụng bộ hấp thụ dao động thụ động có cản đã được Den Hartog [29] nghiên cứu cho trường hợp đơn giản khi hệ chính không có cản nhớt và chịu kích động

của lực điều hòa

F (t) F eIt .

2 o

Bằng cách đặt các hệ số không thứ nguyên

ωa

Ω

: Tỉ số giữa tần số riêng của bộ hấp thụ dao động và hệ chính.

ω

Ω

: Tỉ số giữa tần số lực kích động và tần số riêng của hệ chính.

k1 m





a : tần số dao động riêng của bộ hấp thụ dao động.

k2 M

: tần số dao động riêng của hệ chính.

μ m

M : Tỷ số khối lượng của bộ hấp thụ và hệ chính.

a

c 2m

là tû

số cản nhớt của bộ hấp thụ dao động thụ động.

Khi đó phương trình vi phân dao động (1.9a) trở thành :

1xx2x

F (t) / M

2 1 2

(1.9b)

x x  2x 22x  0

1 2 1 1

Trong ví dụ này, hiệu quả của bộ hấp thụ dao động thụ động được tính thông qua

hệ số A là tỷ số giữa biên độ dao động và chuyển vị tĩnh

x2st

F0 k

Ax2 max

x2st

2

(22)2 (2)2

(  )(1  )  (2) (1 )



2 2

2

2 2

2



2

2 2 2

(1.10)

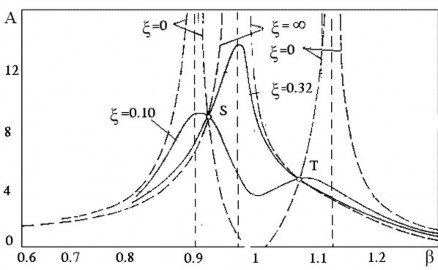
Hình 1.9. Hệ số A theo biến β với μ=0.05, α=1.0.

Hệ số biên độ A là một hàm của 4 tham số μ, α, β, ξ đồ thị của A theo biến β trong trường hợp α=1.0, μ=0.05 và các giá trị khác nhau của ξ được biểu thị trên hình

1.9. Chúng ta hãy quan sát sự thay đổi của A khi tăng dần cản nhớt của bộ hấp thụ dao động thụ động.

Từ đồ thị trên hình 1.9 chúng ta có thể thấy rằng nếu bộ hấp thụ dao động thụ động không có cản nhớt, hệ số A tăng đến vô hạn tại tần số cộng hưởng của hệ chính và tần số cộng hưởng của bộ hấp thụ dao động thụ động.

Khi cản nhớt của bộ hấp thụ dao động thụ động đạt tới vô hạn, hệ chính và bộ hấp thụ dao động thụ động coi như gắn cứng với nhau và trở thành hệ một bậc tự do với khối lượng bằng tổng của hai khối lượng và vì vậy, hệ lại dao động ở chế độ cộng hưởng

tại * 

k1

m  M

. Như vậy ở giữa những điểm cộng hưởng này phải có giá trị nào đó

của mà đỉnh của cộng hưởng là nhỏ nhất.

Như chúng ta đã nói ở trên, mục đích của việc gắn thêm bộ hấp thụ dao động thụ động là giảm đỉnh cộng hưởng của biên độ dao động tới giá trị nhỏ nhất có thể. Từ đồ thị chúng ta có thể nhận thấy có hai điểm (S và T) tại đó hÖ sè A không phụ thuộc vào hệ số cản nhớt và như vậy đỉnh của biên độ dao động nhỏ nhất có thể đạt được bằng cách chọn hệ số f để hai điểm S, T có tung độ bằng nhau và đồ thị biểu diễn giá trị của A đạt giá trị cực đại.

Tại điểm S do có = 0, hệ số A bằng

(2 2 )

(2 2 )(1 2 ) 22

A 

Tại điểm T do có = , hệ số A bằng

1

1 2 1

A 

Đỉnh của biên độ dao động có thể đạt được giá trị nhỏ nhất bằng cách cho tung độ hai điểm S và T bằng nhau và có giá trị cực đại. Để tung độ của hai điểm S và T bằng nhau ta có :