Mô Hình Động Lực Học Của Các Giỏ Đựng Trái Thanh Long Trong Quá Trình Vận Chuyển Trên Ruộng Khi Thu Hái

Nhận xét :

+ Nếu các hk = 0 thì có được:

Bk 0

và Bk = - 1 khi đó hệ (2.64) sẽ trở

thành hệ (2.34) giải cho trường hợp các puli đỡ có độ cao ngang nhau. Điều này càng khẳng định độ tin cậy của công thức tính.

+ Việc tính toán cơ học cho đường cáp khép kín với các trụ đỡ có độ chênh cao được áp dụng hiệu quả khi sử dụng đường cáp để vận chuyển trái cây trong địa hình sườn đồi, khi mà điểm tập kết trái cây ở cao hơn mặt bằng đồng ruộng.

+ Các thông số của đường cáp có các trụ đỡ có có độ chênh cao về độ cao là số liệu đầu vào để tính toán công suất tối thiểu để vận hành đường cáp sau này.

2.4. Mô hình động lực học của các giỏ đựng trái thanh long trong quá trình vận chuyển trên ruộng khi thu hái

Đường cáp khép kín để vận chuyển trái thanh long trên ruộng khi thu hái được thiết kế như hình 2.1. Dưới tác dụng của lực kéo do mô tơ cung cấp, dây cáp di chuyển mang theo các giỏ đựng trái thanh long được liên kết với cáp qua các móc treo. Quá trình di chuyển cáp có hiện tượng vận tốc thay đổi dẫn đến cáp di chuyển có gia tốc thay đổi, cùng với sự tác động của gió thổi trên mặt phẳng ngang nên quá trình di chuyển của các giỏ treo hàng có hiện tượng dao động theo phương ngang và phương dọc theo đường cáp trên các nhịp cáp (hình 2.8). Tại các khu vực cáp di chuyển vòng cũng có sự dao động đáng kể của các giỏ thanh long.

Trong nội dung này, luận án trình bày việc thiết lập hệ phương trình vi phân mô tả sự chuyển động của các giỏ thanh long khi di chuyển ở hai khu vực: trên các nhịp cáp và khi qua khúc cua chuyển hướng cáp.

2.4.1. Phương trình vi phân chuyển động của giỏ đựng thanh long trong các nhịp khi cáp di chuyển có gia tốc và chịu tác động của lực gió theo mặt phẳng ngang

Xét sự di chuyển trong mặt phẳng ngang của các giỏ đựng thanh long khi có

x( t )

lực ngoài là gió tác động và cáp di chuyển với gia tốc .

Xét nhịp cáp có n giỏ đựng thanh long được treo cách đều nhau với một khoảng S (m) tại các điểm Ak. Dây treo giỏ vào cáp dài r (m). Khối lượng mỗi giỏ là m (kg). Lực căng ngang dây cáp là H (N). Lực tác động của gió lên các giỏ đựng

hàng nằm trên mặt phẳng ngang là thời gian (s).

FG ( t )fx( t ), fz ( t )- đơn vị (N), ở đây t –

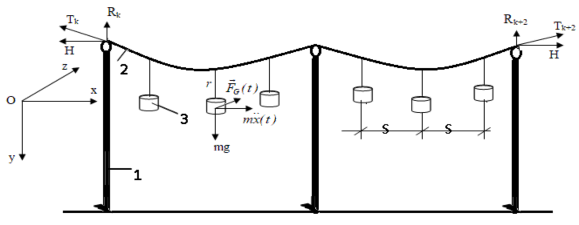
Hình 2.8. Sơ đồ động lực học đường cáp vận chuyển trái thanh long

1- Trụ đỡ; 2- Dây cáp 3- Giỏ đựng trái thanh long.

Đặt : S- Khoảng cách 2 giỏ đựng thanh long;

- Chiều dài nhịp;

Số lượng các giỏ trong nhịp n S ;

FG - Lực tác động của gió vào giỏ đựng trái thanh long;

- Giỏ đựng trái thanh long di chuyển vận tốc v, với gia tốc a = x( t ) ;

- Khối lượng mỗi giỏ đựng trái cây bằng m (kg).

Giả thiết: Bỏ qua trượt của dây cáp với bánh chủ động, bỏ qua sự đàn h ồi và dịch chuyển của trụ đỡ, bỏ qua lực tác động của người đặt trái thanh long vò giỏ chứa.

Lực căng ngang của cáp ở mọi nơi đều bằng H (N) và đã tính toán ở các phần trên.

Phân tích lực theo sơ đồ như hình 2.9, sau đó sử dụng nguyên lý D'Alembert để thiết lập phương trình vi phân chuyển động của các giỏ đựng thanh long.

Gọi Ak - các điểm dây treo giỏ trên cáp , Bk - các điểm treo giỏ

Gọi zk vàvk là khoảng cách của các điểm Ak và Bk với mặt phẳng thẳng đứng đi qua hai puli đỡ cáp của nhịp.

Gọi k

là góc giữa dây treo giỏ và mặt phẳng vuông góc với dây cáp, với

chiều dương ngược kim đồng hồ khi đứng dọc theo trục z nhìn góc k .

Ở đây k  0 , n 1 .

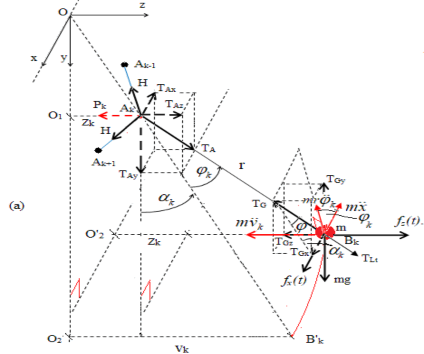
Hình 2.9. Sơ đồ phân tích lực trong tính toán dao động của giỏ đựng thanh long

Chọn hệ tọa độ như hình vẽ: Trục x hướng dọc theo đường thẳng nối hai puli đỡ dây cáp, trục y hướng xuống dưới, trục z vuông góc mặt phẳng thẳng đứng đi qua hai puli đỡ cáp.

Trong nội dung này, ta xét chuyển động của giỏ theo hai phương z và x, tức

là sẽ tìm quy luật theo thời gian của z = z(t) và

( t ) dưới tác động của ngoại

lực gió thổi theo mặt phẳng ngang và cáp chuyển động có gia tốc.

Theo sơ đồ phân tích lực trên hình 2.9, ta có: Tại điểm Ak có :

- Hai lực căng ngang của dây cáp với độ lớn H (N) theo hướng

Ak Ak 1

- Lực căng dây treo giỏ độ lớn TA.

Tại điểm Bk, nơi dây treo giỏ, có các lực tác dụng:

- Lực căng dây TG ( ngược hướng với TA);

x( t )

- Trọng lực mg hướng theo trục y;

Ak Ak 1 và

- Lực quán tính

mx( t ) , do dây cáp di chuyển có gia tốc

nên thông qua

liên kết dây treo giỏ sẽ có lực quá tính của giỏ hàng được sinh ra là

mx( t ) .

- Lực

- Lực

mvk

m rk

hướng theo phương z;

có hướng theo chiều dương của góc

k . Như vậy véc tơ

m rk

nằm trong mặt phẳng Ak Bk B’k ;

- Lực li tâm TLt

được sinh ra khi giỏ chuyển động, lực này hướng ngược với

lực căng dây TG;

- Các thành phần của lực gió ngang fx(t) và fz(t).

Xét tại điểm Ak, hai lực căng ngang dây cáp có độ lớn H sẽ cân bằng với lực căng dây treo giỏ TA.

Để tính hợp lực căng ngang H tại các điểm Ak theo phương z, ta có sơ đồ (b) trên hình 2.9. Chiếu lên phương z, hợp lực Pk được tính :

P H .zk zk 1 zk zk 1 , k  1,n

k s s 



Pk 

H .2z s

k zk 1

zk 1 

, k  1,n

(2.72)

Độ lớn lực căng dây tại Ak là TA . Từ điều kiện cân bằng lực tại Ak theo phương z dẫn đến:

TA .cosk .sink

Pk  0

, k  1,n

Do sink

vk zk

r

và cùng với (2.72) nên :

T .cos

.vk zk 

H.2z z

z  0

, k  1,n

(2.73)

A k r s

k k 1

k 1

Xét tại các điểm treo giỏ Bk, ta có sơ đồ (c) hình 2.9 cho hình ảnh các lực tác dụng lên giỏ hàng có khố lượng m.

Chiếu các lực tác dụng vào giỏ Bk đựng thanh long khối lượng m lên phương z , từ điều kiện cân bằng ta có:

mvk

TGTLt .cosk.sinkmrkcosk

fz ( t )

(2.74)

Xét tam giác vuông IEBk (vuông tại I):

có IBk = BkE. cosk = HK = BkC. cosk .sink

lại có BkE = BkC . cotk

=> cotk . cosk

= cosk .sink

=> cosk =

cosk .sink .tank

sink .sink

Thay vào (2.74) có được:

mvk

TGTLt.cosk.sinkmrksink.sink

fz ( t )

(2.78)

k  1,n

Chiếu các lực tác dụng vào giỏ Bk lên phương y, từ điều kiện cân bằng lực ta được:

TGTLt .cosk.coskmrkcos kmg

(2.79)

Xét tam giác vuông BkQE vuông tại Q: BkQ = BkE. cos k

có BkQ = BkC. cosk .cosk và BkC = BkE. tank

do vậy BkQ = BkC. cosk .cosk = = BkE. tank . cosk .cosk

=> cos k sink .cosk . Thay vào (2.79) có được:

TGTLt .cosk.coskmrksink.coskmg

Thay (2.80) vào (2.78) nhận được:

(2.80)

v 

fz( t )

g. sink

k m cos

, k  1,n

(2.81)

k

Chiếu các lực tác dụng vào giỏ Bk lên phương x, ta được:

mrkcoskfx( t ) TGTLt .sinkmx

Từ (2.80) có được:

(2.82)

TGTLt .sink

mg sink

cosk .cosk

sin2 

k

k

mr .

cosk

(2.83)

Thay (2.83) vào (2.82), nhận được:

mr

mg sink

sin2 

k

k cosk 

fx ( t )



cos

.cos

mrk

cos

.mx

k k k

1  2.sin 

2

k



x

f ( t )

x

cos

k

k

r mr

g.sink

hay

Dẫn đến :

r .cosk .cosk

x 

fx ( t ).

cosk

g.sink1

(2.84)

k r mr  1 2.sin2 

r .cos1  2.sin2 



Chú ý rằng:

k k k

1sin2 

k

v z sin2 

sink k k

r

, do cosk 

1k

2

vz 2

nên:

cosk 1 

k k ;

2r2

2

có:

sink k

, cosk 1k, các độ lớn TA = TG = T.

2

Để đơn giản tính toán, trong (2.73) ta có thể cho T .cosmg . Do đó, từ (2.73), (2.81) và (2.84) dẫn đến hệ phương trình:



mg .vk zk

H .2z z

z  0

( a )





v 

r s

fz ( t )  2r.g.

k k 1

vk zk

k 1

, k  1,n (b)

(2.85)

k m

2r 2vz 2





x f ( t )

k k

2 2 1

k

x

.k 2r.gk

( c )



k k k

k

r mr

 21  2.2 

2r 2 v

z 21  2.2

Từ (a) trong (2.85), đặt

a r .H

mg.s

ta có được:

a.zk1 ( 2a 1) zk

a.zk 1

vk

, k  1, n

(2.86)

Mặt khác: z0 = zn+1 =0 do là tại các điểm trên puli đỡ. Do vậy hệ (2.86) là hệ n phương trình đại số tuyến tính của n ẩn z1, ..., zn được tính theo các trị của v1, v2, ..., vn.

Ma trận hệ số vế trái của (2.86) có dạng:

2a 1	a	0	0	0	0	0
a 	2a 1	a	0	0	0	0

Có thể bạn quan tâm!

• Xây Dựng Mô Hình Tính Toán Cơ Học Đường Dây Cáp
• Tính Toán Một Số Thông Số Cơ Học Của Dây Cáp Chịu Dãn, Trọng Tải Phân Bố Đều
• Tính Phản Lực Tại Các Puli Đỡ Trong Hệ Thống Cáp Khép Kín
• Giải Hệ Phương Trình Vi Phân Dao Động Của Giỏ Đựng Trái Thanh Long
• Độ Vòng F (Cm) Tính Theo Lực Căng Ngang H (N) Và (Cm) Khi Tải Trọng Đều Q = 0.2 (N/cm)
• Khảo Sát Độ Vòng Của Đường Cáp Hai Trụ Đỡ Có Độ Cao Chênh Nhau

Xem toàn bộ 196 trang tài liệu này.







 0 a

2a 1 a

0 0 0 

A 



(2.87)

 0 0 0 0

a 2a 1

a 





Gọi

0 0 0 0 0

a 2a 1

z1 

z2 

Z 







zn 

v1 

v2 

V 

,







vn 

1 

2 



,







n 

(2.88)

thì hệ (2.76) có dạng : A.Z = V (2.89)

Nếu A khả đảo thì Z = A-1. V (2.90)

D1 

D 

D2 

Gọi







Dn 

, với D = V – Z (2.91)

ta đưa hệ (2.85) về dạng:

v fz ( t )  2r.g. Dk

, (1)

k

m



k 2r 2 D2

x f ( t ) 2 2 1 

(2.92)

x.k 2r.gk

( 2 )

k r mr  21  2.2 

2r 2 D2 1  2.2









k k k

k  1, n

Hệ (2.92) là hệ phương trình vi phân tuyến tính cấp 2 với điều kiện đầu tại



t = 0 :

V  0, V  0 ,  0 ,  0

Ta có thể giải hệ (2.92) bằng phương pháp số qua phần mềm Matlab.

2.4.2. Phương trình vi phân chuyển động của giỏ đựng thanh long trong quá trình cáp chuyển hướng và chịu tác động của lực gió theo mặt phẳng ngang

Đường cáp được chuyển hướng như được mô tả trong hình 2.10 (b). Ở đây ta chỉ xét sự dao động của giỏ hàng trong mặt phẳng thẳng đứng vuông góc với đường cáp trong quá trình di chuyển qua khu vực chuyển hướng cáp.

Xét đường cáp di chuyển với vận tốc a = a(t) , lực gió ngang tác động vào giỏ theo phương tâm puli chuyển hướng đến giỏ là f(t) (N).

1- Trụ đỡ , 2- puli chuyển hướng

3- Dây cáp, 4- Giỏ đựng thanh long

(b)

(a)

Hình 2.10. Sơ đồ phân tích lực tác động vào giỏ trong quá trình đường cáp chuyển hướng