Độ Vòng F (Cm) Tính Theo Lực Căng Ngang H (N) Và (Cm) Khi Tải Trọng Đều Q = 0.2 (N/cm)

Bảng 3.2. Độ vòng f (cm) tính theo lực căng ngang H (N) và (cm) khi tải trọng đều q = 0.2 (N/cm)

H (N)

(cm)

3000	3500	4000	4500	5000
2000	33	29	25	22	20
2200	40	35	30	27	24
2400	48	41	36	32	29
2600	56	48	42	38	34
2800	65	56	49	44	39
3000	75	64	56	50	45

Có thể bạn quan tâm!

• Tính Phản Lực Tại Các Puli Đỡ Trong Hệ Thống Cáp Khép Kín
• Mô Hình Động Lực Học Của Các Giỏ Đựng Trái Thanh Long Trong Quá Trình Vận Chuyển Trên Ruộng Khi Thu Hái
• Giải Hệ Phương Trình Vi Phân Dao Động Của Giỏ Đựng Trái Thanh Long
• Khảo Sát Độ Vòng Của Đường Cáp Hai Trụ Đỡ Có Độ Cao Chênh Nhau
• Vùng Tần Số Cộng Hưởng Dao Động Ngang, Dọc Của Giỏ Trên Nhịp
• Sự Ảnh Hưởng Của Độ Dài Nhịp Cáp Đến Biên Độ Cực Đại Của Dao Động Giỏ Đựng Thanh Long

Xem toàn bộ 196 trang tài liệu này.

Nhận xét :

Từ kết quả tính toán được ở bảng 3.1, với các độ vòng f đạt yêu cầu đặt ra trong thiết kế đường cáp thì độ dài L của cáp và khoảng cách giữa hai gối sai khác nhau rất nhỏ (sai khác lớn nhất 0.1%).

Do vậy, giả thiết về tải trọng phân bố đều trên dây cáp được quy về tải trọng phân bố đều trên đường nằm ngang nối giữa hai gối là hợp lý.

3.1.2. Cho trước f , H, q tính L ,

Với các giá trị định trước: cường độ trọng tải q, lực căng ngang H < H giới hạn – của cáp và độ vòng f < f giới hạn – của độ vòng tối đa, ta cần tính toán giá trị L và .

q2



8Hf

q

Do H nên tính được

8 f

có u 4 f 

2qf H



ln u  1 u2

Thay u và vào ta tính được

L 



2 



1 u2 

(3.2)



u 



3.1.3. Cho trước L , , q tính f , H

2L

ln u 4f

Từ (3.2) có được

 1 u2 với

u

u .

1 u2

1 u2

2L ln u 

Đặt

A dẫn đến

W(u) 

1 u2 A  0

u

(3.3)

Tìm gần đúng nghiệm phương trình W(u) = 0 bằng phương pháp chia đôi liên tiếp. Để thực hiện, ta cần xác định khoảng (a, b ) sẽ chứa nghiệm phương trình W(u)=0. Các giá trị a và b cần thỏa mãn:

a) W(a).W(b) < 0

b) W'(u) không đổi dấu u( a, b )

Chú ý rằng do

A  2L

nên A > 2

1 u2

ln u 

Do W(u) 

1 u2 A , nên W(u) > 0 khi

A21

u

1u2

A hay khi u 

( do u > 0)

Như vậy nếu u 

thì W(u) > 0. (3.4)

A21

1u2

Xét hàm (u)  ln u u .

Có (0) 0

1 u2

(u) 1

 1 

0 u

(a)

(b)

1 u2

Từ (a) và (b) => (u)  ln u 

u  0

1 u2

1 u2

ln u 

u 0



hay

ln u 

u

u 0  1

u

u 0

(3.5)

1 u2

ln u 

Có W(u) 

1 u2  1 A

 1. Do có (3.5) nên với

A2  2A

u

1u2

giá trị u thỏa mãn :

 1 A  0

u 

thì W(u) < 0

A2  2A

Như vậy, với u 

Có

thì W(u) < 0 (3.6)

u1

ln u 

ln u 

1 u2

1 u2

1 u2

1 u2

W(u) 

1 u2 u

u2

1 u2

1 ln u 

u u2

1 u2





Do có (3.5) nên

W(u) 



u 



0 u  0

A21

u 

(3.7)

A2  2A

Từ (3.4), (3.6), (3.7) ta lấy: a 

thỏa mãn các điều kiện:

a) W(a).W(b) < 0

, b 

khi đó hàm W(u)

b) W'(u) >0

u( a, b ).

Với điều kiện trên, phương trình W(u) =0 sẽ tồn tại duy và nhất nghiệm trên (a, b). Việc tìm gần đúng nghiệm được thực hiện bằng phương pháp chia đôi liên tiếp.

Sau khi tìm được nghiệm u = u* ta tính :

Tính

f . Tính

.u*

4

H (3.8)

q. 2

8 f

u*

x( x)

khi đó phương trình dây cáp sẽ là: y 

(3.9)

3.1.4. Áp dụng thuật toán chia đôi liên tiếp tìm nghiệm gần đúng độ vòng đường cáp W(u)=0

Với hàm W(u) cùng với các khoảng (a, b) được tìm như đã trình bày ở phần trên, thuật toán chia đôi liên tiếp để tìm nghiệm gần đúng của các phương trình W(u) 0 được thực hiện theo các bước theo bảng sau:

W(u) 0 .

Nội dung
Giá trị A	A  2L
Hàm số	ln u  1u2 W(u)  1 u2 A u
Bước 1	a A2  2A , b A2 1
Bước 2	c a b 2
Bước 3	Nếu W(a).W(c)0 thì b = c, Nếu W(a).W(c)0 thì a = c
Bước 4	Kiểm tra: Nếu | b - a| < sai số thì nghiệm u*a b , dừng 2 tính. Nếu | b - a| > sai số thì quay về bước 3.
Kết quả	.u* .L f  và H  4 2u*

3.2. Khảo sát độ dãn dài của nhịp dây khi chịu tải phân bố đều

Giả sử dây cáp có mô-đul đàn hồi E (N/cm2), diện tích thiết diện ngang là F(cm2).

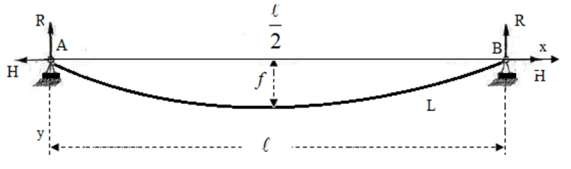
Hình 3.1. Tính độ dãn dài của đường cáp

Xét dây được giữ trên 2 gối ngang nhau với khoảng cách AB = (cm).

Dây có chiều dài L0 (cm), trọng lượng riêng của dây cùng tải trọng theo chiều dài γ (N/cm). Đặt P = γ. L0.

Gọi

u  4 f

, theo (2.19) u sẽ là nghiệm của phương trình :

ln u 

2L

1 u2

1 u2  0

u

(3.10)

Giải (3.10) theo phương pháp lặp. Tính uk ở lần lặp thứ k sẽ là nghiệm của phương trình:

1 u2

k

1 u2 

ln uk

u

k

k

2L(k 1) 0

(3.11)

Lượng dãn dài của đoạn cáp sẽ là:

(k )

q 2 u 2 

- Tính

L 

1 k

- Tính

Lk L0

2E.F.uk  3 

L(k )

Tính toán với cáp

6 , có mô đun đàn hồi E = 1980.104 N/cm2 . Độ dài hai

gối đỡ = 2400 cm. Kết quả độ dài L và độ vòng lớn nhất f ứng với các độ dài ban đầu L0 (cm) và tải trọng phân bố đều q (N/cm) được cho trên bảng 3.4.

Tính toán giá trị u với sai số 10-8 và tính

L với số lần lặp k = 5.

Bảng 3.4. Độ dãn dài

L và độ vòng f theo độ dài ban đầu L0 và tải trọng q

q (N/cm)

0.08		0.1		0.15		0.2
L , f (cm) L0 (cm)	L	f	L	f	L	f	L	f
2400.4	0.8	32.2	0.9	34	1.2	37.7	1.5	40.6
2400.7	0.7	35.5	0.8	37.1	1.2	40.6	1.4	43.4
2401.0	0.6	38.5	0.8	40	1.1	43.2	1.4	45.9

Bảng 3.5. Sai số các giá trị L và f giữa hai lần lặp thứ 4 và 5.

q (N/cm)

0.08		0.1		0.15		0.2
Sai số (cm) L0(cm)	|L5-L4|	|f5 –f4|	|L5-L4|	|f5 –f4|	|L5-L4|	|f5 –f4|	|L5-L4|	|f5 –f4|
2400.4	2.04E-02	8.75E-01	3.16E-02	1.22E+00	6.49E-02	2.08E+00	1.03E-01	2.93E+00
2400.7	5.06E-03	2.58E-01	8.96E-03	4.01E-01	2.29E-02	8.25E-01	4.15E-02	1.30E+00
2401	1.55E-03	9.26E-02	3.04E-03	1.57E-01	9.22E-03	3.72E-01	1.87E-02	6.42E-01

Nhận xét :

Qua kết quả tính toán, nhận thấy rằng: Ở khoảng cách 2400 cm giữa hai giá

đỡ với các độ vòng lớn nhất cho phép

fmax

trong khoảng 30  46 cm

và trọng tải

phân bố đều cường độ q trong khoảng 0,08  0,2 (N/cm) thì độ dãn dài của cáp khá nhỏ (chưa đến 1,5 cm). Từ đó thấy rằng, trong tính toán đường cáp vận chuyển thanh long có thể áp dụng với mô hình dây cáp không chịu dãn, như thế sẽ làm đơn giản trong quá trình tính toán.

3.3. Khảo sát một số thông số động lực học đường cáp khép kín có các gối đỡ có cùng cao độ

Tính toán cho đường cáp khép kín 8 nhịp, với độ dài (cm) giữa các giá đỡ và tải trọng phân bố đều q (N/cm) khác nhau trên các nhịp. Bảng 3.6 cho giá trị độ vòng lớn nhất f tại các nhịp, lực căng dây T, lực căng ngang dây H và các phản lực

R tại các giá đỡ. Trong tính toán này tổng chiều dài cáp

Lk 14505 khoảng cách

giữa các giá đỡ 

k  14500 cm . Áp dụng phương pháp Newton – Raphson, tính

toán với sai số  3.6E 12 .

Cod của chương trình tính được viết trên Matlab với file dữ liệu đầu vào được nhập trên EXCEL nằm trong phần phụ lục. Kết quả tính toán được cho trên bảng 3.6.

Bảng 3.6. Lực căng ngang H và phản lực Ry tại giá đỡ đường cáp khép kín có

cùng cao độ. Tổng 

k 14500cm, Lk

 14505cm

Giá đỡ

1		2		3		4		5		6		7		8		1
(cm)		2000		2000		2100		1000		2200		2100		2100		1000
q (N/cm)		0.2		0.2		0.2		0.2		0.2		0.19		0.1		0.05
f (cm)		25.1		25.1		27.7		6.3		30.4		26.3		13.8		1.6
H (N)		3984		3984		3984		3984		3984		3984		3984		3984
T (N)		3989		3989		3990		3986		3990		3989		3986		3984
Ry (N)	225		400		410		310		320		420		305		130		225

Nhận xét: Từ kết quả tính toán cho ta một số nhận xét sau:

1- Ngoài giá trị của tải trọng q thì khoảng cách giữa các giá đỡ ảnh hưởng rất lớn đến độ vòng cực đại của nhịp cáp. Với tải trọng tương đối đều nhau giữa các nhịp, với tổng độ dài cáp (14505 cm ) lớn hơn tổng độ dài các nhịp đỡ (14500 cm) một khoảng 5 cm và khoảng cách giữa hai nhịp trung bình từ 20 – 22 m thì độ vòng f nằm trong khoảng 1,5 – 31 cm.

2. Với khoảng cách giữa các giá đỡ trong khoảng 2000 - 2200 cm, tải trọng q = 0.2 N/cm, thì với độ vòng trong khoảng 1,5 – 31 cm, khi đó lực căng ngang cáp H đã đạt trên 3984N. Điều này sẽ làm tăng lực kéo ngang đường cáp tại puly chuyển hướng cáp đi vòng. Do vậy, tại đây các trụ đỡ cần được gia cường thêm dây néo.

3. Việc lực căng ngang cáp bị tăng lên lực tác động lên puli chuyển hướng tăng lên, dẫn đến ma sát lăn tăng lên đồng nghĩa với công suất tiêu thụ tăng lên. Khi lực căng ngang tăng độ vòng giảm đi dẫn đến công suất tiêu thụ của hệ thống giảm. Đây cũng là cơ sở để có thể tính giá trị của lực căng ngang H làm cho công suất tiêu thụ của hệ thống đạt cực tiểu.

3.4. Khảo sát giá trị u trong phương trình độ vòng dây tựa trên hai gối có độ cao chênh nhau

Để giải gần đúng phương trình (2.47) bằng phương pháp chia đôi liên tiếp, ta cần tìm khoảng nghiệm cho giá trị u.

Giả sử có một đường cáp mềm tựa trên hai gối O, K có độ cao ngang nhau và

nhận điểm A là điểm có độ vòng lớn nhất f0 = h (như trong hình 3.2 là đường nét đứt), khi đó theo (2.16) trong chương 2 có được độ dài L0 của đoạn cáp OA là :



ln u  1 u2

0



L0 1 



2



1 u2 

0 0 

u 

0 

(3.16)

1

OK

2

với

u  4 f0

2h và

(3.17)

2

0

1 1

1

Chú ý: + Khi u 2h

thì B = 0 nên từ (2.47) ta cũng có được (3.16)

+ Độ dài L đoạn cáp OA luôn phải thỏa mãn điều kiện :

1

2 h2

L 

Sẽ xảy ra các trường hợp:

(3.18)

a) 2 h2 L L như hình 3.2a

1 0

b) L0 < L như hình 3.2b

c) L = L0 đoạn cáp là đoạn nét đứt đậm trên hình 3.2.

ln u  1u2

ln Bu 

1B2u2

Đặt: (u) 

1  1u2 B 

L

(3.19)

1B2u2

2(1B) u u 





Nhận thấy, khi u=u0 thì B(u0) = 0 nên cùng với (3.16) có

(u0 ) L0 L

Để giải gần đúng phương trình

(u)  0 bằng phương pháp chia đôi liên tiếp,

ta cần xác định khoảng chứa nghiệm u.

Tùy theo giá trị của L sẽ dẫn đến một trong các trường hợp sau:

a) Trường hợp 1 : L = L0 khi đó nghiệm u* 2h

1

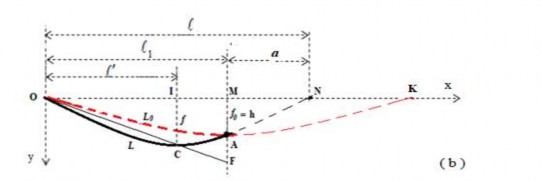
Hình 3.2. Các trường hợp đường cáp tựa trên hai gối có độ chênh cao