Giải Hệ Phương Trình Vi Phân Dao Động Của Giỏ Đựng Trái Thanh Long

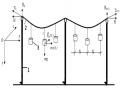
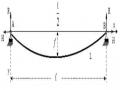
Gọi :- góc lập bởi dây treo giỏ và phương thẳng đứng; d - khoảng cách từ tâm trụ đỡ đến giỏ;

R - bán kính puli chuyển hướng; r - độ dài dây treo giỏ;

m – khối lượng giỏ hàng.

Khi đó tại điểm treo giỏ A, có các lực tác dụng nằm trong mặt phẳng thẳng đứng đi qua trục đỡ và vuông góc với cáp:

- Lực căng dây T và lực ly tâm

mr2

(sinh ra khi giỏ chuyển động theo góc

). Hai lực này ngược hướng nhau và nằm dọc theo dây treo giỏ.

ma2

- Lực li tâm

, có phương vuông góc với trục đỡ, hướng ra ngoài;

- Lực quán tính

mr

, vuông góc với dây treo giỏ;

- Trọng lực giỏ: mg.

Từ điều kiện cân bằng của giỏ trong mặt phẳng thẳng đứng này, chiếu các lực lên

phương của lực quán tính

mr

ta được:

mg sin

ma2



cosmrf ( t ).cos 0

sin2 

(2.93)

Thay d = R + r.sin

và cos 1 vào (2.93), dẫn đến :



ma2 sin2 

sin2 

mg sin 1

( R r.sin)

2 f ( t ).1

2 

mr



g a2

f ( t )

2 



lấy sin

ta được:



r( R r.) 

mr 1 2 

(2.94)



Phương trình (2.94) là phương trình vi phân dao động của giỏ trong mặt phẳng thẳng đứng đi qua tâm puli chuyển hướng và vuông góc với cáp, khi giỏ di chuyển trong khu vực chuyển hướng cáp.

Giải phương trình (2.94) với điều kiện đầu: t = 0 , ( 0 )  0, ( 0 ) 0.

Việc giải các phương trình vi phân trên bằng phương pháp số nhờ Matlab sẽ được trình bầy chi tiết qua các thuật toán ở phần tiếp theo.

2.5. Giải hệ phương trình vi phân dao động của giỏ đựng trái thanh long

2.5.1. Thuật toán giải gần đúng hệ phương trình dao động của giỏ đựng thanh long khi di chuyển trên đường cáp

Như phần trên, luân án đã thiết lập được hệ phương trình vi phân dao động của giỏ đựng thanh long khi di chuyển trên nhịp cáp:

v fz ( t )  2r.g. Dk

, (1)



k 2r 2 D2

x f ( t ) 2 2 1 

x.k 2r.gk

( 2 )

(2.95)

k r mr  21  2.2 2r 2 D2 1  2.2







k k k

k  1, n

Hệ (2.95) là hệ phương trình vi phân tuyến tính cấp 2. Do vậy, để tìm nghiệm gần đúng của (2.95) bằng phương pháp số ta cần đặt biến phụ để chuyển về hệ phương trình vi phân cấp 1, khi đó mới tính toán được bằng phần mền Matlab.

y v

y1 v1



1 1 y v

y2

v1

2 1

y3

y

v2

v

y3

y4

v2



4 2

y v



y v

2n1 n

y2n vn

y 

y 



2n1 1

2n1 1

y 

Đặt:

y2n2

1

<=>

2n2 1

(2.96)

y2n3 2



2n3

2

y2n4 2



2n4 2

y 



y4n1 n



4n1 n

y4n n

4n n

Giả sử ma trận A1 B 

, khi đó hệ (2.95) được đưa về dạng:

i j n n

y1 y2



n

B1 k y2k 1

2 2



y 2rg.k 1

f ( t )

 2r2 n B y m

1 k

k 1



y2i1 y2i



n

2k 1 





2i

Bi k y2k 1

2rg.k 1

f ( t )

 2r2 n B y m



i k

k 1



y2n1 y2n



n

2k 1 



Bnk y2k 1

y 2rg.k 1

f ( t )

2n

n 2 m

 2r2 B y 



k 1

y2n1 y2n2



2k 1



x

f ( t )

2 y2

2r.g y

y2n2 x

.2n12n1

2 2 2

r mr

 2 1 2.y2n1 n

 1 2.y2n1



y2n2i1 

y2n2i

2r2 B y

1 k

k 1

2k 1 



x

f ( t )

2 y2

2r.g y

y2n2i

x.

2n 2i1



2n2i1



2 2

r mr

2 1 2.y2n 2i1 n

1 2.y2n2i1

 2r

Bi k y2k 1 



y4n1 y4n



x

f ( t )

2 y2

k 1 

2r.g y

y4n x

.4n14n1

(2.97)

2 2 2

r mr  2 1 2.y4n1 n

 1 2.y4n1

n k

2r 2 B y

k1

2k 1 





Điều kiện đầu

V( 0 )  0 ; V( 0 )  0 ; ( 0 )  0 ; ( 0 )  0

<=>Y 0 0 (2.98)

Giải bằng số hệ (2.97) với điều kiện đầu (2.98) được thực hiện trên Matlab.

2.5.2. Thuật toán giải gần đúng hệ phương trình dao động của giỏ đựng thanh long khi chuyển hướng chuyển động

Mô hình tính toán dao động của giỏ hàng được xét trong mặt phẳng thẳng đứng vuông góc với cáp trong khu vực cáp chuyển hướng được mô tả trong hình

2.10 và nhận được phương trình vi phân (2.94):

g 

a f ( t )

2 

r r( R r.) mr

1 2 



với điều kiện đầu khi t = 0 : ( 0 )  0, ( 0 ) 0. (2.99)

Để giải bằng số phương trình (2.98) với điều kiện đầu (2.99) ta cần đưa (2.98) về hệ phương trình vi phân cấp 1:

Đặt

y1y1

, khi đó (2.98) sẽ trở thành hệ:



y





2 2 

y1 y2



g a2

f ( t )y2 

(2.100)

y2 y1 

1 1

r r( R r.y1 ) mr  2 

với điều kiện đầu tại t = 0:

y1( 0 ) 0 ; y2( 0 )  0;

(2.101)

Giải bằng số hệ (2.100) với điều kiện đầu (2.101) được thực hiện trên Matlab.

2.6. Tính toán công suất tiêu thụ khi vận hành đường cáp

Để tính được công suất tiêu thụ khi vận hành hệ thống đượng cáp, ta cần tính năng lượng tiêu hao khi sản sinh lực kéo cáp, các lực ma sát tại các puli đỡ, tại các puli chuyển hướng di chuyển vòng. Như vậy, ngoài lực thắng các lực ma sát, ta cần tính được các lực cần có để di chuyển các giỏ đựng hàng.

2.6.1. Công suất tiêu thụ cho việc di chuyển các giỏ đựng thanh long

Xét sự di chuyển của các giỏ đựng thanh long trên một nhịp cáp có hai gối đỡ A và B, hướng di chuyển cáp từ B đến A, ta thấy sẽ xảy ra ba trường hợp sau:

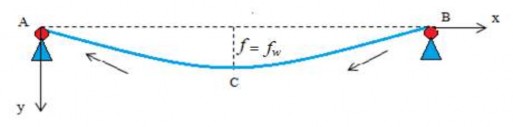
(a)

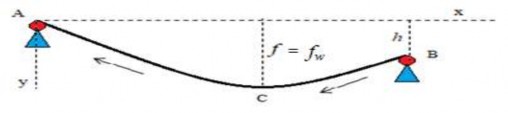
(b)

(c)

Hình 2.11. Mô hình tính công suất tiêu thụ để di chuyển giỏ đựng thanh long trên nhịp cáp

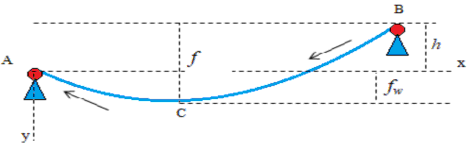
Dây cáp có tải trọng đều cường độ q (N/m), việc giữ các tải trọng này trên cáp là do các lực căng ngang và lực kéo của dây. Do đường cáp khép kín, nên các lực này tự phân phối trên các puli đỡ và lực dãn của cáp, không cần thêm lực ngoài. Để làm di chuyển đường cáp với tốc độ v (m/s), cần có lực sinh công làm di chuyển cáp từ C đến A. Lực sinh công di chuyển cáp từ C đến A được tính theo công thức tích phân đường loại 2.

Fc Q. . ds 0.dx +q.dy

CA CA

qdy q. fw

,( N )

(2.102)

Trong đó: fw là khoảng chênh độ cao của điểm thấp nhất C của nhịp đường cáp và điểm A là điểm puli đỡ đầu di chuyển cáp ra khỏi nhịp.

Q là véc tơ biểu thị cường độ lực (tải trọng) trên đơn vị độ dài dây cáp,

Q Qx, Qy- có đơn vị là N/m. Trong mô hình đường cáp tính toán có Qx= 0 ,

Qy = q, do đó Q 0, q.

ds là vi phân cung, là véc tơ tiếp tuyến cung CA có hướng theo cung từ C đến A.

Do cáp di chuyển với vận tốc v (m/s) nên công suất cần có để di chuyển cáp trên nhịp đỡ là:

(2.103)

2.6.2. Công suất tiêu thụ thắng lực cản ma sát

Giả sử trên puli đỡ cáp chịu phản lực Ry, khi đó lực cản ma sát bằng lực ma sát lăn nên được tính theo công thức:

Fp k R

, (N) (2.104)

với k – Hệ số ma săt lăn, k = 0,01.

Do lực căng dây cáp bằng H, nên lực tác dụng lên vành puli chuyển hướng

theo phương ngang là H . Do vậy, lực ma sát sinh ra do lực ngang này sẽ là:

Fn k 

2 H

, (N) (2.105)

Ở đây, k - Hệ số ma sát lăn, thường lấy k = 0,01.

Giả sử hệ thống cáp có n puli đỡ cáp, có m puli chuyển hướng và cáp di chuyển với tốc độ v (m/s), thì công suất tiêu thụ để thắng ma sát là:

WM nF p

mFn .v

, ( N.m / s)

(2.106)

2.6.3. Công suất tiêu thụ cho toàn hệ thống cáp khép kín

Giả sử hệ thống cáp khép kín có j nhịp cáp, n puli đỡ cáp, m puli chuyển hướng. Tải trọng phân bố đều trên mỗi nhịp và có cường độ qi (N/m) trên nhịp thứ

i. Khoảng chênh độ cao của điểm cáp thấp nhất và puli (ở về phía cáp di chuyển

đến) trong nhịp cáp thứ i là

f (i ) (m). Lực căng ngang dây cáp là H (N). Cáp di

chuyển với vận tốc v (m/s), khi đó tổng công suất tiêu thụ cho hệ thống vận hành:





j n

(i)

W qifw.v

i1

k Rim

i1

2H v , ( Nm / s)



(2.107)

Trong đó

Ri

i1

= R - Tổng tải trọng trên đường cáp.

k - Hệ số ma sát lăn, thường lấy k = 0,01; v - Vận tốc di chuyển của dây cáp

Trong công thức (2.107) có hai thông số phụ thuộc vào nhau, đó là H và

f (i ) .

Hai đại lượng này tỷ lệ nghịch với nhau, do vậy với R, v và các qi không thay đổi thì sẽ có giá trị H phù hợp để cho W là nhỏ nhất. Nội dung này sẽ được khảo sát trong chương sau.

Kết luận chương 2

Từ kết quả nghiên cứu ở phần trên, luận án rút ra một số kết luận sau:

1. Do giới hạn tải trọng trên đơn vị độ dài ( < 20 N/m), nên giả thiết tải trọng phân bố đều với cường độ q = qmax là để tính cho trường hợp tải trọng lớn nhất có thể xẩy ra trong tính toán thiết kế đường cáp, từ giả thiết trên, luận án đã xây dựng được mô hình, thiết lập công thức tính toán độ vòng của đường cáp (f), lực căng ngang (H), độ dãn dài của dây cáp (L), phản lực lên các gối đỡ (R) của đường cáp vận chuyển trái thanh long trong các trường hợp dây cáp có tính đến độ dãn và không tính đến độ dãn, độ cao hai gối đỡ bằng nhau và có có độ chênh cao. Các kết quả đạt được ở nội dung này sẽ là cơ sở để tính toán động lực học của các giỏ đựng trái thanh long khi di chuyển trên hệ thống cáp và cũng là cơ sở để tính toán công suất tiêu thụ khi vận hành đường cáp.

2. Đã xây dựng được mô hình, thiết lập được hệ phương trình vi phân chuyển động của giỏ đựng trái thanh long khi di chuyển trên nhịp cáp và tại khu vực cáp chuyển hướng. Từ kết quả nghiên cứu là cơ sở đề xuất giải pháp hạn chế dao động của giỏ đựng trái thanh long.

3. Đã thiết lập được công thức tính toán công suất tiêu thụ khi vận hành đường cáp vận chuyển trái thanh long, từ kết quả tính toán lựa chọn được công suất động cơ điện hợp lý cho đường cáp.

Chương 3

KHẢO SÁT MỘT SỐ THÔNG SỐ ĐỘNG LỰC HỌC CỦA ĐƯỜNG CÁP VẬN CHUYỂN TRÁI THANH LONG

Từ kết quả về các tính toán nhận được ở chương 2, trong chương này luận án tiến hành khảo sát một số thông số ảnh hưởng đến độ vòng, dao động của đường cáp.

3.1. Khảo sát phương trình độ vòng dây cáp

Các phương trình (2.4) và (2.16) cho liên hệ giữa các đại lượng: L , , f , H. Từ các phương trình liên hệ này, nếu cho trước giá trị hai đại lượng nào đó thì sẽ tính được giá trị hai đại lượng còn lại. Ứng dụng này được sử dụng trong tính toán tối ưu khi thiết kế các đoạn cáp trong thực tế. Ở đây ta xét hai trường hợp có ý nghĩa thực tế.

3.1.1. Cho trước , f , q tính L

Giả sử hai puli đỡ nhịp cáp có độ cao bằng nhau, cách nhau khoảng , trọng lượng P của nhịp cáp được phân bố đều theo có cường độ q, khi đó có:

q P => tính được H q

(3.1)

8 f



4 f

ln u  1 u2

Tính đại lượng

u => tính được

L 



2 



1 u2 



u 



Ta có bảng 3.1 ghi các giá trị tương ứng của L theo các giá trị của f và

Bảng 3.1. Độ dài L (cm) dây cáp tính theo các giá trị của f và

f (cm)

(cm)

15	20	25	30	40
2000	2000.3	2000.5	2000.8	2001.2	2002.1
2200	2200.3	2200.5	2200.8	2201.1	2201.9
2400	2400.2	2400.4	2400.7	2401	2401.8
2600	2600.2	2600.4	2600.6	2600.9	2601.6
2800	2800.2	2800.4	2800.6	2800.9	2801.5
3000	3000.2	3000.4	3000.6	3000.8	3001.4