Khảo Sát Độ Vòng Của Đường Cáp Hai Trụ Đỡ Có Độ Cao Chênh Nhau

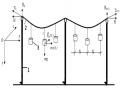
b) Trường hợp 2 : 2 h2 L L

, hình 3.2 (a)

h 1

u 1 h

0

1 h  0

h

1

u

1 0

Do có a 

nên luôn có u =>

(3.20)

Trên hình 3.2.a, nhận thấy:

h f

1



2h 2 f 4 f u

1



AM FI

CI 

(3.21)

OM OI OI

1 0

Từ (3.20) và (3.21) dẫn đến khi 2 h2 LL

thì

h u  2h

1 1

(3.22)

Nhận thấy khi

u h

thì

B(u) 

sẽ bằng 1, do đó u h

là điểm

1

2h  1

u 1

1

gián đoạn của hàm

(u) .

1

Gọi

u h

, có :

1

limB(u)  lim 2h  1 1,

limB(u)  lim 

u2

2h  2

1

u

1

(3.23)



Xét

u u1

lim (u) =

u u1

u u1 u 1 

u u1

u u1

 lim

 ln u 



1

 1u2

B1B2u2





1u2 ln Bu 

1B2u2



L



u u1 2 

(1B)

u(1B) 



 1u2 B 1B2u2

ln u 

1u2 ln Bu 

1B2u2 

1 lim  lim L



2 u u1 

(1B)

u u1

u(1B) 



1 u2

B 1 B2u2



Xét I1 = lim .

u u1 

(1 B) 

1B2u2

Từ (3.23), nhận thấy khi u u1 thì tử thức và mẫu thức đều 0, do đó áp dụng L’hopital ta được:

1u2

B

1B2u2



B 2uB2 2u2BB

I1  lim

u u1

(1B)

 lim u 

1u2

2B 1B2u2

u u1 B

Kết hợp với (3.23) có được :

I1 

1  2u1

(3.24)

Xét

I2 

lim

u u1

ln u 

 ln Bu 

1 u2

1

1 u2

1 B2u2

u(1 B)

Nhận thấy khi L’hopital ta được:

u u1

thì tử thức và mẫu thức đều 0, do đó áp dụng

I2 

ln u 



lim

u u1



 ln Bu 

1 u2

u(1 B)

B B u 



uB2 u2 BB

1 B2u2

Bu  1 B2u2

1 



1 B2u2







1 

 lim 

1 u2  1



u u1 u 

1 u2

 (1 B uB)



1



Sử dụng (3.23) ta được:

I2 



(3.25)

1 u2

1

Từ hai kết quả (3.24) và (3.25) có được :

1

2 

 1  2u

1

1 u2

1

lim (u) 

1 L L

u u1



1

1 u2

1

1 u2 

1 

Như vậy, ta được:

1 u L 

2

1

1 L 

h2

2 2

1

1

2

1

1

h L

lim (u) 

u u1

Đặt :



1u2 B

1B2u2

ln u 

1u2 ln Bu 

1B2u2

1 

L khi u u

2 

(1B)

u(1B) 1





(u) 





2 h2 L khi u u

1 1

thì hàm

(u) sẽ liên tục trên [u1 , u0 ].

Kết luận: Với điều kiện 2 h2 L L

(a)

1 0

thì

(u ) 2 h2 L  0

(b)

trong đó : u1 

1 1

h ,

1

u  2h

0

1

(u0 ) L0 L

 0 . (c)

Do vậy, phương trình

(u)  0 sẽ có nghiệm trên [u1 , u0 ].

Do tính duy nhất nghiệm của bài toán cơ học về độ vòng dây mềm, nên với

điều kiện 2 h2 L L

phương trình

(u)

= 0 sẽ có duy nhất nghiệm

1 0

trên [u1 , u0 ].

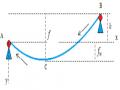
c) Trường hợp 3 :

L0 L

, hình 3.2 (b)

Do a= MN < IN =OI < OM = 1 =>

h 1

1



u h

2h u

1

1 1

a 

(3.26)

Đặt

u  2h

. Có

(u

) L

L  0

(3.27)

1

0

Do B(u) 

0 0

2h  1

u 1

nên với điều kiện (3.26) có được:

-1< B < 0 và 2 > 1 - B > 1 (3.28)

Với điều kiện (3.26) và (3.28) luôn có:

+)

dẫn đến

u 

1u2

1 u2

ln u 

u

Bu 





1B2u2

1 B2u2

ln Bu 

u

 0 u u0

(3.29)

1B2u2



+) B  0

(3.30)

Như vậy sẽ luôn có :

1

u  1 u2

1 B2u2

1  lnB

 0

u u0

(3.31)

2(1 B) 

u Bu 

1 B2u2

Do có (3.28) nên11 u2 11u2

(3.32)

2(1B) 4

1

4

1u2

2

Vậy nếu giá trị u2 > u0 mà thỏa mãn L

(3.33)

thì sẽ có được:

(u2 ) 0

Giải (3.33) ta được

u2  (3.34)

16L2 

1

2

1

Ta cần chứng minh u2 > u0.

Khi L > L0 ta có đường cáp qua hai gối O và A (như hình 3.2.b). Có được các hệ thức: h = MA < MF

OF 2OM 2

h 

Dựa vào các tính chất của các đường thẳng song song, do IM < IN = OI nên:

CF < OC => CF + OC < 2. OC => OF < 2. OC

Mà OC < đoạn cáp OC < L do đó:

OF 2OM 2

2

4.OC2 

1

2 

4L2 

1

2 

4L2 1

4

h 

2h

1

2

1

2



4L2 1

4

16L2 

1

2

1

=> => u2 > u0 .

Kết luận: Với điều kiện L > L0 thì hàm

(u)

thỏa mãn điều kiện:

1



2h

+ (u0 ) 0 , u0

16L2 

1

2

1

+ (u ) 0 , u 

2 2

+ liên tục trên [u0, u2],

Cùng với tính chất duy nhất nghiệm của bài toán độ vòng dây mềm, dẫn đến

phương trình

(u) 0 có duy nhất nghiệm u* trong [u0, u2].

3.5. Khảo sát độ vòng của đường cáp hai trụ đỡ có độ cao chênh nhau

Bài toán khảo sát cho dây cáp có khoảng cách hai nhịp = 2500 (cm), với các độ cao chênh nhau h(cm) = [ 10, 20 , 40, 50] ứng với các độ dài cáp L(cm)

= [ 2501 , 2501.4, 2501.7 ] và ở tải trọng đều q = 0,2 (N/cm).

Việc tính toán thực hiện trên Matlab cho kết quả trên bảng 3.7 và đồ thị ứng với L = 2501 (cm), h= 10 (cm) được cho trên hình 3.3. Ở đây Rc và Rt là phản lực theo chiều đứng tại các gối đỡ cao và thấp, đại lượng f * là sự chênh về độ cao giữa điểm thấp nhất của nhịp cáp và puli gối đỡ điểm cao của nhịp cáp.

Bảng 3.7. Tính độ vòng f , Rc, Rt trên nhịp cáp có gối có độ cao chênh nhau

h = 10 cm			h = 20 cm			h = 40 cm			h =50 cm
Dây cáp (cm)	f * (cm)	Rc (N)	Rt (N)	f * (cm)	Rc (N)	Rt (N)	f * (cm)	Rc (N)	Rt (N)	f * (cm)	Rc (N)	Rt (N)
2501	26	271	229	20	293	207	9	349	151	4	394	106
2501.4	31	267	233	26	286	214	15	329	171	9	358	142
2501.7	35	266	234	30	282	218	19	319	181	13	343	157

Có thể bạn quan tâm!

• Mô Hình Động Lực Học Của Các Giỏ Đựng Trái Thanh Long Trong Quá Trình Vận Chuyển Trên Ruộng Khi Thu Hái
• Giải Hệ Phương Trình Vi Phân Dao Động Của Giỏ Đựng Trái Thanh Long
• Độ Vòng F (Cm) Tính Theo Lực Căng Ngang H (N) Và (Cm) Khi Tải Trọng Đều Q = 0.2 (N/cm)
• Vùng Tần Số Cộng Hưởng Dao Động Ngang, Dọc Của Giỏ Trên Nhịp
• Sự Ảnh Hưởng Của Độ Dài Nhịp Cáp Đến Biên Độ Cực Đại Của Dao Động Giỏ Đựng Thanh Long
• Phương Pháp Xác Định Các Đại Lượng Nghiên Cứu Và Thiết Bị Đo

Xem toàn bộ 196 trang tài liệu này.

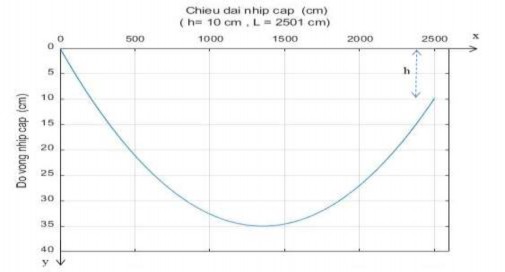
Hình 3.3. Đồ thị phương trình độ vòng dây cáp khi gối đỡ có độ cao chênh nhau

3.6. Khảo sát một số thông số động lực học đường cáp kép kín các giối đỡ có độ cao chênh nhau

Áp dụng phương pháp Newton-Raphson để tìm nghiệm gần đúng hệ (2.63) sẽ dẫn đến giải liên tiếp hệ phương trình đại số tuyến tính (2.64).

Trên bảng 3.8 là kết quả tính toán cho đường cáp khép kín với các thông số như sau: khoảng cách , độ cao chênh nhau giữa hai trụ đỡ h, tải trọng q trên các

nhịp, lực căng ngang H = 3767 N đều bằng nhau trên các nhịp cáp được cho trong bảng, tổng khoảng cách các trụ đỡ đường cáp 50000 cm, tổng độ dài dây cáp là 50024 cm. Kết quả tính toán về độ vòng f , độ dài L cáp cho mỗi nhịp, lực căng dây cực đại T, phản lực R tại các gối đỡ được thể hiện trong bảng 3.8.

Bảng 3.8. Kết quả tính cho đường cáp khép kín với 23 nhịp, độ dài 50000 cm

(cm)	q (N/cm)	h (cm)	L (cm)	f * (cm)	H (N)	T (N)	R (N)
1	2200	0.2	0	2201.3	32.1	3767	3773	315
2	2000	0.2	10	2001.0	21.8	3767	3773	401
3	2100	0.2	15	2101.1	22.3	3767	3774	402
4	2300	0.15	-5	2300.8	23.9	3767	3771	418
5	2200	0.2	0	2201.3	32.1	3767	3773	384
6	2100	0.2	20	2101.2	20.1	3767	3775	394
7	2100	0.2	0	2101.1	29.3	3767	3772	456
8	2000	0.2	-10	2001.0	21.8	3767	3773	429
9	2100	0.2	0	2101.1	29.3	3767	3772	391
10	2200	0.2	0	2201.3	32.1	3767	3773	430
11	2100	0.2	0	2101.1	29.3	3767	3772	430
12	2400	0.2	0	2401.6	38.2	3767	3774	450
13	2300	0.2	-20	2301.5	25.8	3767	3776	503
14	2100	0.15	0	2100.6	22.0	3767	3770	355
15	2400	0.1	0	2400.4	19.1	3767	3769	278
16	2200	0.15	0	2200.7	24.1	3767	3770	285
17	2500	0.2	0	2501.8	41.5	3767	3775	415
18	2100	0.2	0	2101.1	29.3	3767	3772	460
19	2200	0.2	0	2201.3	32.1	3767	3773	430
20	2400	0.2	0	2401.6	38.2	3767	3774	460
21	1800	0.2	-10	1800.7	16.8	3767	3772	441
22	2300	0.1	0	2300.4	17.6	3767	3768	274
23	1900	0.1	0	1900.2	12.0	3767	3768	210

+ Giá trị độ vòng f (cm) trong bảng 3.8 là khoảng cách của điểm thấp nhất trong nhịp cáp so với puli cao nhất đỡ nhịp cáp.

+ Giá trị phản lực gối đỡ theo chiều đứng R (N) là tổng hai phản lực của puli đỡ hai nhịp cáp.

3.7. Khảo sát dao động của giỏ đựng trái thanh long

Hệ phương trình vi phân động lực học (2.95) biểu diễn sự dịch chuyển của giỏ đựng thanh long trong quá trình cáp di chuyển có tính đến sự tác động của lực gió ngang và gia tốc của cáp khi di chuyển. Theo cách thiết lập, ta có 3 bậc tự do cho mỗi giỏ treo trên cáp: Hai khoảng cách từ mặt thẳng đứng trung hòa đến giỏ và đến điểm dây treo giỏ vào cáp, góc lệch của dây treo giỏ với mặt phẳng vuông góc với cáp. Như vậy với mỗi nhịp có n giỏ được treo thì ta phải giải đồng thời 3n giá trị ẩn cần tìm cho một thời điểm t. Chính vì vậy, hệ (2.95) được đưa về hệ phương trình vi phân cấp một (2.97) để giải bằng Matlab.

Mặc dù mô tơ điện dùng để kéo cáp có sử dụng biến tần để có được tốc độ quay ổn định, nhưng do quá trình di chuyển qua các puli đỡ, các móc treo giỏ làm vận tốc di chuyển cáp bị chậm lại và sau khi qua puli thì lại trở lại bình thường.

Chính vì điều này sẽ làm cho cáp di chuyển với gia tốc

x( t )  0 , gây ra lực quán

tính theo phương dọc cáp. Do vậy khi nghiên cứu dao động của giỏ đựng thanh long cũng phải kể đến thành phần này. Để đơn giản trong tính toán, nội dung này sẽ tính

x( t )

toán với thay đổi trong khoảng [a, b] nào đó.

Ký hiệu các thông số:

n – số giỏ treo trên một nhịp cáp; H – lực căng ngang cáp, (N);

S – khoảng cách treo giỏ trên cáp, (m); r – độ dài dây treo giỏ, (m);

m - khối lượng giỏ đựng thanh long, (kg); g – gia tốc trọng trường, (9,80 m/s2);

f ( t ) fx( t ) , fz ( t )

- lực gió trong mặt phẳng ngang với các thành

x( t )

phần theo phương x và phương z. Các hàm fx(t) và fz(t) có dạng sin, đơn vị (N). t – thời gian (s);

- gia tốc chuyển động của dây cáp, (m/s2).

Tính toán cho một nhịp cáp dài 24 m, số giỏ treo n = 30 với khoảng cách treo các giỏ S = 0.80 m. Khối lượng mỗi giỏ m = 2 kg. Tính toán số nhằm mục tiêu khảo sát:

- Vùng tần số mà lực gió sẽ gây cộng hưởng;

- Biên độ dao động cực đại của các giỏ đựng thanh long;

- Sự ảnh hưởng của lực căng ngang H đến tần số, biên độ cực đại của dao động giỏ đựng thanh long;

- Sự ảnh hưởng của độ dài r (đoạn treo giỏ đựng thanh long vào cáp) đến biên độ cực đại của dao động giỏ đựng thanh long.

Quá trình tính toán là thực hiện giải hệ phương trình (2.95) đã được chuyển về hệ phương trình vi phân cấp một (2.97). Các tính toán được thực hiện trên Matlab.

Trong tất các tính toán trong chương này nếu các thông số là cố định thì sẽ được tính với các trị số sau:

+ Nhịp cáp dài 24 m, số giỏ treo n = 30;

+ Khoảng cách treo các giỏ S = 0.80 m;

+ Khối lượng mỗi giỏ m = 2 kg;

+ Độ dài dây treo giỏ r = 0,3 m;

+ fz(t) = a.*rand * sin( 1 t) – có biên độ là số ngẫu nhiên a [0, 4];

+ fx(t) = b.*rand * sin( 2 t) – có biên độ là số ngẫu nhiên b [0, 0.4];

x( t )

+ = c.*rand* sin( 3 t) – có biên độ là số ngẫu nhiên c [0, 1];

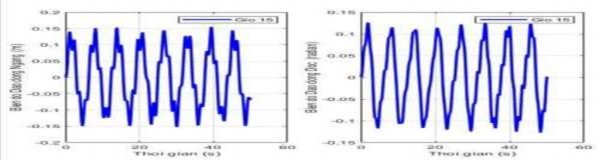
Hình 3.4 Đồ thị biểu diễn dao động của giỏ ở vị trí giữa nhịp cáp

3.7.1. Khảo sát miền cộng hưởng của dao động giỏ đựng trái thanh long

3.7.1.1. Xét quá trình giỏ dịch chuyển trên nhịp cáp

Theo chương 2, ta có hệ phương trình vi phân biểu diễn dao động của giỏ khi cùng cáp di chuyển trên nhịp cáp - phương trình (2.92). Trong phương trình (1) của hệ không chứa các thành phần phụ thuộc vào k- biểu diễn chuyển dịch dọc theo x