Tính Toán Một Số Thông Số Cơ Học Của Dây Cáp Chịu Dãn, Trọng Tải Phân Bố Đều

T

T

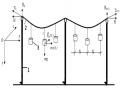
Hình 2.3. Dây cáp tựa trên hai gối ngang nhau

Do dây chỉ chịu lực kéo T (không uốn, không xoắn) nên momen tại điểm

x

bất kỳ M(x,y) đều bằng 0, do vậy sẽ có:

x2

Có thể bạn quan tâm!

• Tời; 2- Dây Cáp Mang; 3- Dây Cáp Nâng Tải; 4- Xe Treo; 5. Dây Cáp Kéo Xe Treo
• Thông Số Kỹ Thuật Của Hệ Thống Đường Cáp Vận Chuyển Thanh Long
• Xây Dựng Mô Hình Tính Toán Cơ Học Đường Dây Cáp
• Tính Phản Lực Tại Các Puli Đỡ Trong Hệ Thống Cáp Khép Kín
• Mô Hình Động Lực Học Của Các Giỏ Đựng Trái Thanh Long Trong Quá Trình Vận Chuyển Trên Ruộng Khi Thu Hái
• Giải Hệ Phương Trình Vi Phân Dao Động Của Giỏ Đựng Trái Thanh Long

Xem toàn bộ 196 trang tài liệu này.

Hy Rx q(x t)dt  0

0

=> Hy Rx q  0

2

(2.1)

Chiếu các lực lên trục y ta được:

R (2.2)

q

2

Từ (2.1) và (2.2) ta có phương trình độ vòng

(2.3)

y qx( x)

2H

Từ (2.3) nhận thấy độ vòng lớn nhất tại

x .

q2

2

Vậy

f yMax 8H

và H 

q2

8 f

(2.4)

4 f x( x)

2

Thay (2.4) vào (2.3) được phương trình độ vòng của dây căng ngang chịu tải trọng bản thân dạng:

y 

2.2.1.2. Tính lực căng dây T

(2.5)

T

T

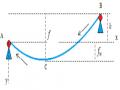
Hình 2.4. Mô hình tính lực căng của dây cáp

Xét tại điểm M(x,y), tại đây lực căng trong dây T nằm theo phương tiếp tuyến

với đường cong của dây

y qx(

x)

.

2H

Gọi α là góc lập bởi T với phương ngang, như vậy tanα = y'(x).

Tại M(x,y) có lực căng ngang là H1, như vậy T

H1



cos

(2.6)

Bằng cách áp dụng các tính toán như trên phần thiết lập phương trình độ vòng

1  2x

cho đoạn dây MN có độ dài và độ vòng lớn nhất tại điểm giữa là

f1 

f y , ta có được công thức dạng (2.4), tức là :

q 2

H1 1

8 f1

(2.7)

Vậy

Luôn có 1

T 

q(  2x)21

8( f

1 tan2 



y) cos

1  ( y '(x))2



(2.8)

Từ (2.5) có:

cos

4 fx( x) 2  4x  4x2 

2

f .

2

f . (  2x)

2

2

f y f 

Thay vào (2.8) được:

q  2x21

q2

8 f

1 y 'x

2

T 

(2.9)

8f ycos

Từ (2.5) được

y4 f (

2

 2x)

q2

8 f

1 

16 f 2

4

 2x

2

Vậy T 

q2

f q

(2.10)

2



8H

do f yMax 8H =>

1 

q2

4H 2

 2x

2

L

=> T H

với q nên

T H

1 

2 L2 

4H 2 

1 2

x 2





Nhận xét:

q2

Lực căng trên dây nhỏ nhất tại

x T H

2 min 8 f

(2.11)

Lực lớn nhất tại gối:

x  0, x

=>

hay

Tgoi 

q2

8 f

1 

16 f 2

2

2 L2

1 

4H 2

Tmax 

hay

Tgoi H

(2.12)

(2.13)

P

8 f

1 

16 f 2

2

2.2.1.3. Tính độ dài dây cáp (L)

Độ dài đoạn cáp L được tính :

4 f (

2

 2x)



L 

4

0

1 y2 dx

16 f 2 2

(2.14)

với y 

, do đó

L 1 

0

(  2x) dx

(2.15)

Tính tích phân (2.15), nếu đặt

u  4 f

thì độ dài



ln u  1 u2

Nhận xét:

L 



2 



1 u2 



u 



(2.16)

Với giả thiết dây mềm không chịu dãn và chịu tải phân bố đều cường độ q (N/m), luận án đã thực hiện được:

+ Thiết lập được phương trình độ vòng y = y(q, , H, x) (2.3) hay dạng y = y (q, , f , x) (2.5);

+ Tính được lực căng dây T = T(q, , H, x) hay dạng T =T (q, , f , x);

+ Bằng cách đặt biến mới

u  4 f

, luận án đã đưa ra được công thức tường

minh về liên hệ giữa độ dài dây cáp L, độ dài nhịp cáp và độ vòng ở giữa nhịp f, đây cũng là điểm mới trong tính toán của luận án.

2.2.2. Tính toán một số thông số cơ học của dây cáp chịu dãn, trọng tải phân bố đều

2.2.2.1. Tính độ dãn dài của nhịp dây khi chịu tải phân bố đều

T Giả sử dây cáp có mô-đul đàn hồi E (Pa), diện tích thiết diện ngang là F(Tm2).

Hình 2.5. Tính độ dãn dài của cáp

Xét dây được giữ trên 2 gối ngang nhau với khoảng cách AB = (m).

Dây có chiều dài L0 (m), trọng lượng riêng của dây cùng tải trọng theo chiều dài γ (N/m). Đặt P = γ. L0.

Giả thiết:

+ Trọng lượng bản thân của dây và tải trọng được phân bố đều theo trục ngang

với cường độ q (N/m) =>

q P ;

+ Có tính đến sự dãn của dây do trọng tải gây ra.

Gọi: R là phản lực theo phương đứng và H là phản lực theo phương ngang tại các gối đỡ, y là độ vòng của dây => y = y(x).

Gọi f là độ vòng tại điểm giữa đoạn dây cáp AB. Từ kết quả bài toán khi cáp chưa dãn:

+ Theo (2.5) có được phương trình dây cáp theo khoảng cách giữa hai gối và độ vòng f tại điểm giữa :

4 f x( x)

2

y (2.17)

+ Theo (2.10) có lực căng cáp tại điểm có tọa độ x là:

q2

8 f

1 

16 f 2

4

 2x

2

T (2.18)

+ Gọi

u  4 f

thì u sẽ là nghiệm

ln u 

2L

1 u2

1 u2  0

u

(2.19)

Do lực căng dây T = T(x) là hàm của tọa độ x, nên ứng suất kéo của dây cũng

q 2

8F. f

1 

16 f 2

4

 2x

2

T (x)

là hàm của x , tức là

(x) 

F

Do vậy, phân tố độ dài s

tại điểm x sẽ có độ dãn dài

(x)s

E

, tức là:

q 2 16 f 2 2

 1 

8E.F. f

4  2xs

(2.20)

Do đó, độ dãn dài của đoạn cáp sẽ là:

L

L ds 

0

dx (2.21)

Thay

y4 f (

q2

8E.F. f



0

1 

16 f 2

4

 2x

2

. 1y

2

 2x)

vào (2.21) ta được:

8E.F. f 1 

q2



0



2

16 f 2 2 

L 

q2

8E.F. f







x 

8 f 2

3

4

 2x



3 



0

1

8E.F. f

q3



16 f 2 



3 2 



L 

4  2x

dx



(2.22)

hay

L 

2E.F.u 1  3

q2



u2







(2.23)

Dẫn đến độ dài đoạn dây cáp sau khi chịu dãn sẽ là:

Ld L0 L

(2.24)

Ở đây L0 là độ dài đoạn dây cáp khi chưa chịu tải trọng (tức là lực căng dây bằng 0 tại mọi điểm). Giá trị u là nghiệm của phương trình (2.19) với L được thay bởiLd. Vì vậy, giá trị u được tìm gần đúng bằng phương pháp lặp.

2.2.2.2. Phương pháp lặp để tính độ dãn dài của nhịp cáp căng ngang.

Với độ dài L= Ld được tính

Ld L0 L

thì giá trị f đã thay đổi cũng

được thể hiện trong (2.19) khi L được thay bởi Ld. Do vậy, để tính L sẽ dẫn đến công thức tính lặp giải phương trình (2.19) như sau:

+ Tại lần lặp thứ 0 lấy L= L0, ở đây L0 là độ dài cáp khi chưa có tải.

+ Tại lần lặp thứ k :

1 u 2

k





- Tính giá trị uk từ phương trình (2.19):

W(u ) 

ln uk 

1 u 2 

2Lk 1  0

(2.25)

u

k k

k

k 1k 1

L2

L

L2

2

, b 

4k 11

2

W(uk ) 0

được giải gần đúng bằng phương pháp chia đôi liên tiếp, với

khoảng nghiệm ban đầu [a , b], trong đó

a  2

(k )

q 2 u 2 

- Tính

L 

1 k

(2.26)

- Tính

Lk L0

2E.F.uk  3 

L(k )

(2.27)

Vòng lặp sẽ dừng lại khi

Nhận xét:

Lk Lk 1 

- là sai số định trước.

Nội dung tính toán cơ học cho đường cáp chịu dãn sẽ được khảo sát ở chương sau với đường cáp có các thông số vật liệu cụ thể. Căn cứ vào kết quả tính toán độ dãn của cáp khi chịu tải trọng đều lớn nhất, từ đó có thể bỏ qua hoặc phải tính đến sự dãn của cáp trong các tính toán đường cáp.

2.2.3. Tính toán một số thông số cơ học của đường cáp không dãn, khép kín có nhiều nhịp đỡ có cùng cao độ, chịu tải phân bố đều có cường độ khác nhau trên các nhịp

Qua thực tế và khảo sát trực tiếp từ các phương trình tính toán độ dãn dài của nhịp cáp khi chịu tải tối đa (nội dung này được thực hiện ở chương sau), nhận thấy: với loại cáp sử dụng trong hệ thống có thể bỏ qua sự dãn dài trong quá trình tính toán. Vì vậy, tính toán cơ học cho hệ thống cáp khép kín sẽ không kể đến sự dãn dài của cáp khi chịu tải.

Đường cáp không chịu dãn, khép kín được đỡ bởi các các puli tại n cột đỡ có độ cao ngang nhau. Thứ tự các cột đỡ là A1, A2, ..., An. Gọi khoảng cách giữa cột đỡ

k

AkAk+1 là , trên nhịp cáp này chịu tải phân bố đều có cường độ qk .

Do khoảng cách giữa các nhịp khác nhau cũng như cường độ qk khác nhau trên từng nhịp, nên có độ vòng fk tại các nhịp là khác nhau. Do tại các cột dùng puli đỡ cáp, nên lực căng ngang dây cáp đều bằng nhau tại tất cả các puli đỡ. Sử dụng điều kiện này, ta thiết lập hệ phương trình để tính toán các độ vòng fk cũng như các phản lực liên kết tại các puli đỡ.

qk

qk

Hình 2.6. Mô hình tính toán đường cáp khép kín

2.2.3.1. Thiết lập hệ phương trình tính

Từ (2.4) có lực căng ngang của cáp tại puli đỡ có độ cao ngang nhau là

q 2 q

u  4 f

H 

8 f 2u

với

. Do lực căng ngang tại các puli đỡ đều bằng nhau

nên có :

H 

qk

k , k 1n

2uk

(2.27)

hay

qk k qk 1 k 1

, k 1 

(n 1)

(2.28)

2uk 2uk 1

dẫn đến hệ các phương trình:

uk 

uk 1

, k 1 

(n 1)

(2.29)

k

ở đây

u  4 fk

qk k

k

là các ẩn cần tìm.

qk 1

k 1

Hệ phương trình (2.29) mới có n-1 phương trình để tìm n giá trị uk ta có thêm điều kiện: Tổng độ dài các đoạn cáp trên các nhịp bằng độ dài đường cáp cho trước:

L1 + L2 + ... + Ln = L. (2.30)

Theo (2.16) có độ dài đoạn cáp trên nhịp thứ k là:



ln u  1 u 2

L k  1 u 2 

k k 

(2.31)

k 2 k



u 

k 

k

Như vậy, với là hằng số thì Lk là hàm của uk . Từ các phương trình (2.29),

(2.30), (2.31) dẫn đến hệ phương trình tính các uk sau:

u1 u2  0

q q

1 1 2 2

u2 u3  0

q q



2 2 3 3

 ......

u u

(2.32)

n1

n 0

qn1





n1

qn n

L1L2 ...LnL

với Lk được cho bởi (2.31).

Hệ phương trình (2.32) là hệ phương trình đại số phi tuyến. Để giải gần đúng ta dùng phương pháp Newton – Raphson.

2.2.3.2. Áp dụng phương pháp Newton – Raphson giải hệ phương trình

Hệ phương trình (2.32) được viết dưới dạng:

1 (u)  0



2

 (u)



 0

......

(2.33)





n1





(u)  0

trong đó

(u)  0

uk qk



k

uk 1 qk 1 k 1

k (u) 

; (u) 

n

Lk(u) L

k 1

với u 

u1 ,u2 , ...,un 

. Hệ phương trình (2.33) gồm n phương trình để giải

ra n ẩn u1, ...,un chưa biết.

1

Sử dụng phương pháp lặp Newton – Raphson giải hệ (2.33) dẫn đến hệ phương trình ở lần lặp thứ i là:

h



1 1

q

1

1 1

q

2

2 2

h



 (u(i1) )

q

2

2 2

q

3

3 3







......

1 h 1 h

2

(u(i1) )

 1 1









(u(i1) )

(u(i 1) )

h h

q

n1

n1 n1

q

n

n n

(u(i1) )



n1

n

(u(i 1) ) (2.34)

(i1)

u

h1 u

h2 

...

u

hn L Lk (u )

1 2

(i1)

u(i1)

n

u(i1)

k 1

với

k (u

) kk 1,

k qk 1 k 1

qk

k  1 (n 1)