Tính Phản Lực Tại Các Puli Đỡ Trong Hệ Thống Cáp Khép Kín

u



ln u(i1) 

 1  (u(i1) )2

k

L (u(i1) ) 

k 1  (u(i1) )2 k 

k

Có thể bạn quan tâm!

• Thông Số Kỹ Thuật Của Hệ Thống Đường Cáp Vận Chuyển Thanh Long
• Xây Dựng Mô Hình Tính Toán Cơ Học Đường Dây Cáp
• Tính Toán Một Số Thông Số Cơ Học Của Dây Cáp Chịu Dãn, Trọng Tải Phân Bố Đều
• Mô Hình Động Lực Học Của Các Giỏ Đựng Trái Thanh Long Trong Quá Trình Vận Chuyển Trên Ruộng Khi Thu Hái
• Giải Hệ Phương Trình Vi Phân Dao Động Của Giỏ Đựng Trái Thanh Long
• Độ Vòng F (Cm) Tính Theo Lực Căng Ngang H (N) Và (Cm) Khi Tải Trọng Đều Q = 0.2 (N/cm)

Xem toàn bộ 196 trang tài liệu này.

(i1)

2 k





(i1)

(i1) 

k 



k

1 (u )

(i1) 2

k

1 (u(i 1) )2

k

ln u(i1) 

(u )Lk (u

) k 

u u

2 u(i1)

(u(i 1) )2 

k k k k 

và u(i) 

u(i1) h ,

k 1n

k k k

Ở đây có thể lấy

u(0) 

u (0) ,u (0) , ...,u (0) 

từ nghiệm các phương trình:



1 2 n

 1 (u(0) )2

k

ln u(0) 

L (0) k 1 (u(0) )2 k 

(2.35)

u

k 2 



trong đó

k

k

L (0) 

L

n

k

, k  1n

i



i1

(0) 

k 

(2.36)

Luôn có

n

i

k

k

L do đó luôn thỏa mãn Lk 

i1

i  1

i

n

h

2

Quá trình lặp được dừng khi thỏa mãn điều kiện:

 cho trước.

Sau khi tính được các uk , ta tính được độ vòng fk , độ dài dây cáp Lk tại các nhịp cũng như các phản lực Rk tại các gối đỡ.

2.2.3.3. Tính phản lực tại các puli đỡ trong hệ thống cáp khép kín

Đối với hệ thống cáp khép kín, các puli gối đỡ có độ cao ngang nhau, nhịp cáp thứ k có cường độ tải trọng đều qk . Theo sơ đồ đường cáp khép kín hình 2.6 thì cột puli đỡ cáp thứ k sẽ có phản lực là tổng phản lực hai nhịp cáp thứ k-1 và thứ k ,

tức là R

R(k 1)

R(k )

y y y

Ở đây, chúng ta sẽ có :

R(k 1) và R(k ) 

qk 1 k 1

qk

k

y 2 y2

Sử dụng công thức tính toán này để tính bền cho trụ đỡ và puli đỡ cáp cũng như tính lực ma sát tại các puli đỡ khi cần tính công suất kéo dây cáp.

Nhận xét:

4 fk

k

Tính toán cơ học cho đường cáp không chịu dãn, khép kín, tựa trên n trụ puli gối đỡ cao ngang nhau, khi sử dụng điều kiện lực căng ngang bằng nhau tại tất cả các puli đỡ và điều kiện tổng độ dài đường cáp bằng L sẽ có được n phương trình để

xác định n giá trị

uk . Từ đó có thể xác định các thông số fk , Lk , Rk , H, Tk

tại các nhịp cáp. Đây là các giá trị đầu vào để tính bền cho các chi tiết khác trong hệ thống cáp: Hệ thống giá đỡ cáp di chuyển thẳng, di chuyển vòng, puli đỡ, tính toán công suất mô tơ kéo cáp, tính dao động của giỏ hàng khi cáp di chuyển...

2.3. Tính toán một số thông số cơ học của dây cáp không dãn, tựa trên các gối có cao độ lệch nhau, chịu tải phân bố đều

Xây dựng phương trình dây cáp mềm tựa trên hai gối có độ cao chênh nhau được giải quyết dựa trên mô hình và kết quả của bài toán dây cáp mềm căng ngang tựa trên hai gối cùng cao độ.

2.3.1. Tính toán một số thông số cơ học của dây cáp không dãn, tựa trên hai gối có cao độ lệch nhau, chịu tải phân bố đều

2.3.1.1. Phương trình độ vòng dây mềm tựa trên hai gối có độ chênh cao

Dây mềm có độ dài L được căng trên hai gối tựa O và A. Điểm A có độ cao thấp hơn điểm M (M ngang bằng với O) là h(m). Khoảng cách OM là 1 (m). Dây chịu tải phân bố đều theo chiều ngang với cường độ q (N/m).

Để thiết lập phương trình độ vòng của đoạn dây OA, ta sử dụng mô hình sau: Xét đoạn dây mềm chịu tải phân bố đều theo chiều ngang với cường độ q (N/m). Đoạn dây này được tựa trên hai gối ngang nhau tại điểm O và N. Độ dài đoạn dây này và điểm N cần được tính toán sao cho dây đi qua điểm A và hai đoạn

dây trùng nhau trong khoảng OA (hình 2.7).

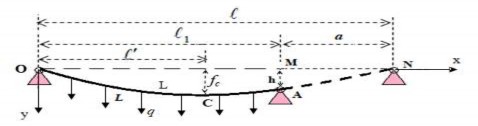
Hình 2.7. Mô hình tính độ vòng dây tựa trên các gối có độ cao lệch nhau

Chọn trục tọa độ như hình vẽ: Gốc O trùng với puli đỡ cao, trục Ox nằm ngang và trong mặt phẳng thẳng đứng chứa 2 gối đỡ, trục Oy hướng xuống dưới.

Gọi : khoảng cách ON là (m),

fc là khoảng chênh độ cao từ C điểm thấp nhất của dây với puli đỡ đầu cao của nhịp cáp.

Khi đó, theo (2.5) có phương trình độ vòng của dây sẽ là :

4 fc x( x)

2

y (2.37)

Độ dài đoạn dây OA bằng L nên sẽ có:

1 2 1 16 f 2 2

4

L 1y dx 

4 f

c

2

 2x

0 0

1c

 2xdx

(2.38)

Đặt t 

4 fc

, x t 

4 f

c

1

2

 2

1



x  0 t 

=> dt 8 fc dx ,

2

(2.39)

Dẫn đến :

L

2



8 fc

4 fc 2

c

2



4 f

1 

1 t2

dx

(2.40)



1

Gọi a 

, tính tích phân (2.40) được:

1 t 2

4 fc

( 1 a)

4 fc a1 

( 1 a)2

( a)2 t 2 1 

L 1

1 t 

ln t 

(2.41)

8 fc  2 2 

hay: (2.42)

( a)2 2 f

16 f 2

1 4 f

16 f 2

L 1

1c

lnc

1c

8 f ( a) ( a)2 2 ( a) (

a)2

1 1 1 1

2 f a 

16 f a 

2

1

( a)2

1

c



1

2



1 4 f a 

lnc 1 1c 1

16 f 2 a 

2





1

( a)4

1

2 ( a)2

1

( a)4

1







1 a

Đặt u 

4 fc

khi đó từ phương trình độ vòng của dây (2.37) có được:

do đó :

h u.

y u. x(

1 a x) ( 1 a)

(2.43)

(2.44)

1( 1 a 

( 1 a)

1) u.

1.a

( 1 a)

Dẫn đến có được các hệ thức sau:

h 2h u 2 u 2

a 1; a 1 1 1; a 1 1;

(2.45)

u 1 h u 1 h u

1 h

a  2h u 2 2h

Đặt

B(u) 

11 1 1

(2.46)

a u 2 u

1 1 1

khi đó hệ thức (2.42) sẽ là: (2.47)



ln u  1u2

ln Bu 

1B2u2

1B2u2

L 1  1u2 B 

2(1B) u u 





Giải phương trình (2.47) tìm được u, cùng với (2.45) thay giá trị u và a vào (2.43) ta được phương trình biểu diễn độ vòng của dây căng trên hai gối có độ chênh cao.

2.3.1.2. Tính lực căng dây, lực căng ngang và phản lực theo phương thẳng đứng tại các gối đỡ

Sau khi giải được u từ phương trình (2.47), thay vào biểu thức tính giá trị của

h 1

u*

1

h

a . Thay các giá trị này vào phương trình độ vòng (2.43) ta được độ

vòng y của dây cáp phụ thuộc vào x :

* x( a x) *

u*x2

y u .1u x 

(2.48)

( 1 a) ( 1 a)

a) Lực căng ngang cáp tại các puli đỡ cáp (H)

Theo (3.1) có được lực căng ngang H tại các puli đỡ cáp là:

2

H q

8 fc

h

q

2u*

q 

1 a

2u*

1

1 h

q2

(2.49)

1 h

Thay a 1

u*

vào (2.49) ta được: H 

2u*

(2.50)

b) Lực căng dây (T)

Lực căng dây T tiếp tuyến với dây nên nếu gọi là góc hợp bởi tiếp tuyến và phương Ox thì:

T H H

cos 

1y2

* 2u* x

(2.51)

( 1 a)

Từ phương trình (2.48) có được:

y u 

(2.52)

=> y(0) 

u* ;

y(

1) 

u* 

(2.53)

2u*

1

( 1 a)

u* 

a 



a 

1 u*.B*

1 

với

B* .

a 

a 

1

1

Dẫn đến: + Tại puli đỡ cao

+ Tại puli đỡ thấp

T H

1u*2

1u*B*2

T H

(2.54)

(2.55)

c) Tính phản lực theo phương đứng tại các puli đỡ (Ry)

Phản lực Ry theo phương đứng tại các puli đỡ ở giá cao và thấp có trị số khác nhau. Phản lực Ry được tính theo công thức:

Ry

Theo (2.53) có được:

H. y

(2.56)

+ Tại puli giá đỡ cao:

+ Tại puli giá đỡ thấp:

R H.u*

y

y

R H.u* B*

(2.57)

(2.58)

2.3.2. Tính toán một số thông số cơ học đường dây cáp khép kín tựa trên các gối có độ cao lệch nhau, chịu tải phân bố đều có cường độ khác nhau trên các nhịp

Đường cáp khép kín được đỡ bởi các các puli tại n cột đỡ có độ chênh cao. Thứ tự các cột đỡ là A1, A2, ..., An. Độ cao chênh lệch giữa hai puli đỡ Ak và Ak+1 là hk , khi đó hk > 0 nếu Ak+1 thấp hơn Ak và hk < 0 nếu Ak+1 cao hơn Ak. Gọi khoảng cách giữa cột đỡ Ak và Ak+1 làk , độ dài dây ở nhịp cáp này là Lk , trên nhịp cáp

n

này chịu tải phân bố đều có cường độ qk . Chú ý rằng luôn có

2 h2

k k

An1 A1 .

hk 0 do

k 1

Điều kiện (3.18) được thể hiện ở đây qua biểu thức :

Lk 

Tương tự như trong trường hợp đường cáp khép kín tựa trên các puli đỡ có độ cao ngang nhau. Trong trường hợp này mặc dù có sự chênh nhau về độ cao của các puli đỡ cáp và có sự khác nhau về cường độ tải phân bố đều trên các nhịp dẫn đến các độ vòng fk (lớn nhất trên các nhịp) khác nhau, nhưng lực căng ngang dây cáp đều bằng nhau tại tất cả các puli đỡ. Đây cũng là điều kiện quan trọng để thiết lập hệ phương trình tính toán các thông số cơ học cho đường cáp khép kín.

2.3.2.1. Thiết lập hệ phương trình

Sử dụng điều kiện: lực căng ngang dây tại tất cả các puli đỡ đều bằng nhau,

2

kk

q

k hk 



theo (2.50) ta có lực căng ngang

H 

2 uk

(2.59)

Do đó

q 2

k kk 1 k 1

k hk 

2uk 1 k 1 hk 1 

, k

2uk

2

q

 1(n 1)

dẫn đến : (2.60)

 (u ,u

,...u ) 

uk k hk

uk 1

k 1 hk 1  0 ,

k  1(n 1)

k 1 2 n q 2 q2

k k k 1 k 1

Nếu gọi Lk là độ dài đoạn cáp trên nhịp thứ k thì ta có:

ln u  1 u2

1B2u2

k



L k  1u2 k k B

2.61

k 2(1B ) k u k

k k



ln Bkuk

1B2u2

k k









uk 



n

Do Lk

k 1

L nên dẫn đến :



n ln u  1u2

ln B u  1B2u2

k  1u2 k k B

k k k k

1B2u2

k



L  0

(2.62)

n 2(1B ) k u k u 

k 1 k 

k k 



Từ (2.60) và (2.62) ta có hệ phương trình để giải ra các uk :

 (u ,u ,...u ) 

uk k hk

uk 1

k 1 hk 1  0 ,

k  1 (n 1) (2.63)

k 1 2 n q 2 q 2

k k k 1









k 1



n ln u 1 u2

ln B u  1 B2u2

k  1 u2 k k B

k k k k

1 B2u2

k



L  0

n 2(1 B ) k u k u 

k 1



k 

k k 

2hk

uk

 1

k

trong đó Bk theo (2.46) sẽ là: Bk .

Tìm các uk từ hệ (2.63), tính được các giá trị

H , Rkyc , Rkyt ,

Tkyc , Tkyt

2.3.2.2. Giải gần đúng hệ (2.63) bằng phương pháp Newton-Raphson

Áp dụng phương pháp Newton-Raphson để tìm nghiệm gần đúng hệ (2.63) sẽ dẫn đến giải liên tiếp hệ phương trình đại số tuyến tính:

Nghiệm gần đúng lần lặp thứ i của uk sẽ là: u(i) 

u(i1) 

, k 1n

với các αk là nghiệm của hệ:

1

q



1

1



1 1

q



2

2 2







k k k

1

 (u(i1) )

1

q



1

2





3

2 2

q

3 3



2





(u(i 1) )

...... (2.64)

 1 1



qn1





n1

n1 

qn n

n n1

(u(i1) )

(u(i1) ) 

n

(u(i1) ) 

(u(i1) ) 



(i1)

u

1 u

2 ...

u n

L Lk (u )

1 2

n k 1

(i 1)

u(i1)

u(i 1)

h h 

trong đó

k (u

) kk 1kk 1,

k  1 (n 1)

q q q 2 q 2

k k k 1 k 1 k k k 1 k 1 

k

k

L (u(i1) ) k V ,

k 1 n

2(1Bk )

L (u(i 1) ) 2 h

u(i1)



k k

u(i 1) h

k



k k

u h

(i 1)

k 

k k k. Vk

k. Vk ,

k 1 n

với

uk4

2 

1 (u(i 1) )2

k

1 B u



(i1) (i1) k k



2

ln u(i 1) 

k

V  1 (u(i 1) )2

B(i1)

u

k k (i 1)

k

ln B(i1)u(i 1) 

k

1B(i1)u(i1) 2

k k k k 





u

(i 1)

k

1 (u(i 1) )2

k



B  2u B

(i1)

k

k k

(i 1) (i1) 1  (u(i 1) B(i1) )2





k k

V 

k u(i 1) u(i 1)

k k

1 (u(i 1) )2

k

1 (u(i 1) B(i1) )2

k k

k

k k

ln u(i 1) ln u(i 1) B(i1) 



(u(i 1) )2

(u(i 1) )2

k k

B

k

và (i1) 

2hk

u

(i1)

k k

 1 ;

B(i1) 

2hk

Ở đây có thể lấy

u(0) 

u (0) ,u (0) , ...,u (0) 

k

từ nghiệm n phương trình:

k k

(u(i1) )2

1 2 n

 1  (u(0) )2

k

1 B u



(0) (0)

k k



2

ln u(0) 

k  1  (u(0) )2 k

B(0)

(2.65)

2(1 B(0) ) k

u(0) k

k 

k

ln B(0)u(0)  1 B(0)u(0) 2

k k k k 

L(0)  0

u



(0) k

k



k

2h L

2 h2

k k

u(0)

B

trong đó

(0)

k

k

 1;

L (0) 

k k,



n

2 h2

i i

i 1

k  1 n

(2.66)