Khái Niệm Cơ Bản Của Mô Hình Merton

Altman. Mô hình của Altman (1993) đã điều chỉnh mô hình Z-score nguyên gốc: loại ra biến X5 (DT/ TTS) để tối thiểu hóa ảnh hưởng của ngành mà có nhiều khả năng xảy ra khi một biến ngành nhạy cảm như vòng quay tài sản được đưa vào. Mô hình này khá hữu ích trong ngành công nghiệp nơi mà các loại tài sản tài chính khác nhau rất nhiều giữa các doanh nghiệp và các điều chỉnh quan trọng như vốn hóa cho thuê không được thực hiện. Altman (1993) cũng dùng các giá trị sổ sách thay cho các giá trị thị trường.

Hộp 1: Ý kiến chuyên gia về việc lựa chọn mô hình kế toán

TS Nguyễn Thị Thủy (Đại Học Quốc Gia Hà Nội)- Người đã tham gia nhiều công trình nghiên cứu về các mô hình dự báo vỡ nợ doanh nghiệp như đề tài cấp Bộ (2017): xây dựng bộ tiêu chí xác định “ngưỡng doanh nghiệp đệ đơn phá sản” hạn chế hiện tượng vỡ nợ dây truyền trong nền kinh tế Việt Nam. Các nghiên cứu của TS Thủy về dự báo vỡ nợ doanh nghiệp chủ yếu theo phương pháp tiếp cận kế toán:

Mô hình Z- Score (1968) là mô hình đã được áp dụng nhiều trên thế giới, mặc dù mô hình cũng mong muốn sử dụng thêm phần biến thị trường nhưng khi thực nghiệp trong những năm gần đây ở các thị trường cho thấy tính hiệu quả của mô hình không cao và đã được điều chỉnh bởi nhiều nghiên cứu sau này. Trong các nghiên cứu theo hướng kế toán thì mô hình Z – Score (1993) được cho kết quả tương đối tốt khi áp dụng vào dự báo vỡ nợ các doanh nghiệp ở các nước và cũng cần có các nghiên cứu thực nghiệm để có thể áp các mô hình dự báo vỡ nợ doanh nghiệp tại Việt Nam.

TS Thủy cũng đưa ra ý kiến hiện nay cần có thêm các nghiên cứu theo hướng kế toán như Logit, Probit để đưa ra mô hình phù hợp dự báo vỡ nợ cho doanh nghiệp Việt Nam.

Mô hình dự báo Z-score (1993) của Altman:

Có thể bạn quan tâm!

Xem toàn bộ 186 trang tài liệu này.

Z= 6,567X1 + 3,26X2 + 6,72X3 + 1,05X4

Trong đó: Z = Chỉ số tổng hợp X1 = VLĐ / TTS

X2 = LN giữ lại / TTS

X3 = LN sau thuế và lãi /TTS

X4 = GTSS của Vốn CSH / GTSS của tổng nợ

Từ mô hình Z-score bốn biến được điều chỉnh của Altman năm 1993, biến vốn lưu động trên tổng tài sản hay X3 là một thước đo của tài sản lưu động ròng (ví dụ tài sản ngắn hạn nhỏ hơn nợ ngắn hạn) của doanh nghiệp liên quan tới tổng giá trị vốn hóa.

Ông kết luận rằng tỷ số này có giá trị nhất trong các tỷ số thanh khoản trong dự báo vỡ nợ. Tỷ số này cung cấp sức mạnh dự báo cao hơn so với hai chỉ số thanh khoản khác (tỷ số khả năng thanh toán hiện hành và tỷ số khả năng thanh toán nhanh). Độ tuổi của một doanh nghiệp là mặc nhiên được xem xét trong X2, lợi nhuận giữ lại/ TTS. Tỷ số này cho thấy rằng các doanh nghiệp hoạt động lâu năm hơn thường có mức lợi nhuận tích lũy cao hơn. Altman (1968) lập luận rằng các công ty có độ tuổi hoạt động thấp hơn hoặc quy mô nhỏ hơn thường có khả năng bị phân loại vào nhóm vỡ nợ cao hơn. Nhiều nghiên cứu đã cho thấy tỷ lệ phá sản có liên quan chặt chẽ với tuổi của doanh nghiệp.

Chỉ số X3 cho thấy khả năng tạo thu nhập từ tài sản trước khi có bất kỳ sự ảnh hưởng nào của các yếu tố về thuế và đòn bẩy. Tỷ số này dường như đặc biệt phù hợp với các nghiên cứu về dự báo vỡ nợ doanh nghiệp. Altman (1968) đã cho rằng tỷ số này được chứng minh là nhân tố đóng góp quan trọng nhất đối với hiệu quả phân tích khác biệt của mô hình. Tỷ lệ giá trị sổ sách của vốn chủ sở hữu trên giá trị sổ sách của tổng nợ hoặc X4, là yếu tố đóng góp quan trọng thứ ba. Tỷ số này là một thước đo giá trị thuần cho cả các khoản nợ ngắn hạn và dài hạn. Tỷ lệ này chiếm 22,4% hiệu quả phân tích khác biệt của mô hình.

Kết quả khi áp dụng mô hình, nếu Z-score nhỏ hơn 1,10 thì công ty có khả năng đệ đơn phá sản. Z-score giữa 1,10 và 2,60 được xác định là vùng màu xám. Các doanh nghiệp có Z-score trên 2,60 được phân loại như các doanh nghiệp khỏe mạnh hoặc các doanh nghiệp không có nguy cơ phá sản (Altman, 1993). Trong nghiên cứu áp dụng phân loại nếu Z - score nhỏ hơn 1,10 thì doanh nghiệp vỡ nợ.

2.2.2. Mô hình dự báo theo thị trường

Các mô hình về sau trong cách tiếp cận thị trường được phát triển với các giả định ngày càng hoàn thiện hơn so với mô hình gốc là mô hình Merton (1974) trong đó một trong những mô hình được sử dụng phổ biến nhất là mô hình KMV. Mô hình Merton (1984) đặt ra giả định như sau:

❖ Tài sản của doanh nghiệp được giao dịch trên thị trường hoàn hảo, không có kinh doanh chênh lệch giá (Arbitrage). Giá trị tài sản của công ty có thể quan sát được tại bất kì thời điểm nào.

❖ Giá trị tài sản tại thời điểm T theo phân phối chuẩn loga với giá trị trung bình

uT và phương sai O2T

❖ Biến động lợi suất của tài sản là cố định và không phụ thuộc vào biến động tình hình kinh tế và chu kì kinh doanh.

❖ Bảng cân đối kế toán của doanh nghiệp được đơn giản hóa trong đó nợ chỉ bao

gồm trái phiếu doanh nghiệp không trả lãi.

❖ Lãi suất sử dụng là lãi suất phi rủi ro r và cố định tức là không có rủi ro lãi suất trong mô hình.

● Xây dựng mô hình

Giả sử một doanh nghiệp có tài sản được định giá hôm nay là Ao, giá trị trong tương lai tại thời điểm t là At. Mô hình đặt giả thuyết là lợi suất của tài sản theo phân phối chuẩn (Normal distribution) và biến động theo phương trình chuyển động Brown (Brownian motion fomulation)

Trong đó:

= + (4)

+ A: độ lệch chuẩn của tài sản và cố định

+ : hằng số cố định

+ dz: giá trị ngẫu nhiên theo phân phối chuẩn tắc (Standardize normal distribution)

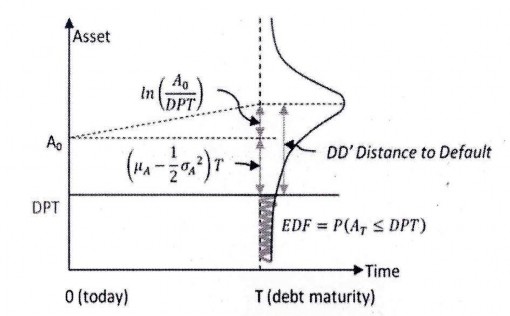
Hình 2.2. Khái niệm cơ bản của mô hình Merton

Do đó, giá trị tài sản tuân theo phân phối loga khuếch tán chuẩn (Lognormal diffusion process) với độ biến động cố định.

{ − +

(5)

√

Với A0 là giá trị tài sản tại thời điêm t=0, giá trị kì vọng của tài sản tại thời điểm t là:

=(6)

Trong điều kiện thị trường hoàn hảo, không có chi phí giao dịch, thuế và thông tin bất cân xứng, giá trị của công ty chỉ phụ thuộc vào cơ cấu vốn của doanh nghiệp tức là bằng tổng nợ và vốn chủ sở hữu. Từ đó mô hình giả định doanh nghiệp chỉ có vốn chủ sở hữu và nợ (Trái phiếu doanh nghiệp không trả lãi), công ty không trả cổ tức, trái phiếu doanh nghiệp có kì hạn T và mệnh giá là K.

Kí hiệu, A0 là giá trị tài sản của doanh nghiệp tại t=0 và AT là tại t=T. Eo là giá trị vốn chủ củu doanh nghiệp tại t=0 cà ET là tại t=T. Nếu tại thời điểm t =T, giá trị tài sản đủ để trả khoản phải trả (mệnh giá D) (AT > K) thì doanh nghiệp sẽ trả nợ, trái chủ sẽ nhận được mệnh giá là K và cổ đông sẽ nhận phần tiền còn lại sau khi trả nợ là AT -

K. Ngược lại, nếu giá trị tài sản thấp hơn khoản phải trả (AT < K) thì doanh nghiệp sẽ không trả nợ và vỡ nợ, trái chủ lúc đó sẽ nhận khoản tiền bằng tài sản của doanh nghiệp là AT còn cổ đông thì không nhận được gì. Như vậy, có thể coi vốn chủ sở hữu của doanh nghiệp như một quyền chọn mua kiểu Châu Âu (European call option):

= {0

Và khoản nợ của doanh nghiệp như sau:

= {!

- Khi AT < K (7)

- Khi AT < K

- Khi AT < K (8)

- Khi AT < K

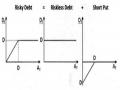
Hay có thể viết lại là DT = K - Max(0, K - AT) tương đương với việc vay khoản K với lãi suất phi rủi ro và bán quyền chọn bán kiểu Châu Âu (European put option).

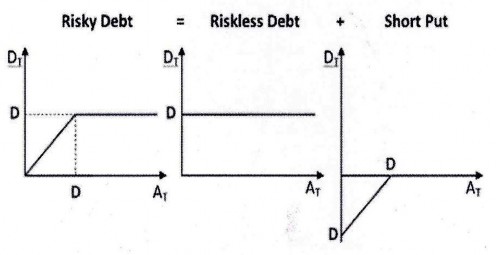
Hình 2.3. Vị thế tương đương khi nắm giữ nợ

Sau đó áp dụng công thức Black, Scholes và Merton vào định giá quyền chọn

bán trong công thức (8) ta có:

PUT = ! "# − − # − $ 9 &' &' + ( + 1+

= ! 2

√

&' &' + ( + 1+

= ! 2

= −

Trong đó

$ √

√

+ E0: Giá trị thị trường vốn chủ tại t=0

+ A0: Giá trị thị trường tài sản tại t=0

+ A: Độ lệch chuẩn của tài sản

+ E: Độ lệch chuẩn của vốn chủ

+ K: Tổng nợ của công ty

+ T : Thời gian trái phiếu đáo hạn

+ R: Lãi suất phi rủi ro

+ N(*): Hàm phân phối chuẩn tích lũy (Cumulative normal distribution function) Từ đó thay giá trị tính từ công thức (9) vào (8) ta được

D0 = Ke-rT - PUT (10)

Hạn chế lớn nhất khi áp dụng mô hình Merton trong thực tế là giá trị tài sản A0 và độ lệch chuẩn A đều không quan sát trực tiếp được, tuy nhiên ta có thể dùng giá trị thị trường cổ phiếu của doanh nghiệp để ước lượng những đại lượng này. Giả sử cổ phiếu của doanh nghiệp giao dịch trên thị trường. Kí hiệu E0 là giá trị vốn hóa thị trường và E là độ lệch chuẩn của vốn chủ. Để xác định được A0 và A, bước đầu tiên phải xác định được giá trị Eo. Theo Hillegeist et al. (2004), có thể dùng giá trị thị trường cổ phiếu của doanh nghiệp để ước lượng những đại lượng này. Giả sử cổ phiếu của doanh nghiệp giao dịch trên thị trường. Kí hiệu E0 là giá trị vốn hóa thị trường và

E là độ lệch chuẩn của vốn hóa thị trường, trong đó E0 được tính bằng giá cổ phiếu tại ngày giao dịch cuối cùng trong năm nhân với số lượng cổ phiếu có quyền biếu quyết đang lưu hành tại thời điểm kết thúc năm kế toán.

Từ công thức số (7) ta có:

Khi AT < K

Khi AT > K

= − !

Áp dụng công thức Black, Schole, Merton vào công thức (7)

E0 = CALL = A0N( $− ! " # 11

(7)

Bên cạnh đó:

# $

Sau đó, giải đồng thời (11) và (12) để xác định A0 vàcó thể tính bằng phương pháp căn chỉnh (Calibration) = phương pháp Merton.

● Ứng dụng của mô hình.

Thứ nhất, mô hình Merton được ứng dụng để đo lường rủi ro vỡ nợ (Credit spread). Kí hiệu D0 là giá trị thị trường của nợ tại t=0, như vậy giá trị của tài sản sẽ bằng tổng nợ và vốn chủ.

A0 = D0 + E0 (13)

Thay công thức (13) vào (15) ta có:

D0 - A0 - A0N(d1) + Ke-rTN(d2) =A0 (1-N(d1)) - Ke-rTN(d2)

= A0N(-d1)+Ke-rTN(d2)

Mà D0 = Ke-yT, trong đó y là lợi suất đáo hạn của khoản nợ Từ đó:

Ke-yT = A0N(-d1) + Ke-rTN(d2)

↔ y = - $&' -# − $ + "# 14

Như vậy ta có thể xác định được rủi ro vỡ nợ bằng cách lấy lợi suất của trái phiếu rủi ro trừ lợi suất của trái phiếu phi rủi ro

S= y - r (15)

Thứ hai, xác suất vỡ nợ được xác định theo công thức sau:

Prob (AT < K) = 1 - prob (AT ≥ K) = 1 - N (e2) (16)

Hay Prob(AT ≥ K) = N(e2)

Trong đó

&' &'

+ 0 − 1 −

$ =

√"

= $ − √ −

Thứ ba là tính toán lỗ kỳ vọng và giá trị hiện tại của lỗ kì vọng Ta có lỗ kỳ vọng là: KN(— e2) — Ateu(T-t)N (-e1) (17)

Giá trị hiện tại của lỗi kỳ vọng là: Ẽ (K —D (T,T))e_r(T-t) (18)

Trong đó Ẽ (.) là giá trị kỳ vọng nhưng sử dụng xác suất trung hòa rủi ro.

Mô hình mở rộng KMV lựa chọn đại diện cho cách tiếp cận thị trường:

Theo mô hình Merton, mệnh giá của khoản nợ được coi như ngưỡng chặn so sánh với tài sản để quyết định doanh có vỡ nợ không. Công ty KMV đã quan sát mẫu gồm hàng trăm doanh nghiệp và nhận thấy rằng một doanh nghiệp thường sẽ vỡ nợ khi giá trị tài sản đạt tới một điểm nhất định nằm giữa nợ ngắn hạn (Short-term debt) và tổng nợ (Total liabilities). Như vậy nếu chỉ sử dụng một minh tồng nợ như trên thì đo lường xác suất vỡ nợ sẽ không được chính xác. Do đó, mô hình KMV đã thêm một đại lượng là điểm vỡ nợ (Default Point). Theo mô hình KMV, điểm vỡ nợ được ước lượng xấp xỉ bằng nợ ngắn hạn và một nửa của nợ dài hạn

DPT = STD + 0.5*LTD (19)

Trong đó

+ DPT: điểm vỡ nợ

+ STD: Nợ ngắn hạn

+ LTD: Nợ dài hạn

Bên cạnh đó, trước khi tính toán xác suất vỡ nợ, bước đầu tiên KMV còn tính thêm một đại lượng nữa gọi là khoảng cách tới điểm vỡ nợ (Distance to Default (DD)). Khoảng cách tới điểm vỡ nợ là khoảng cách giữa giá trị tài sản kì vọng của doanh nghiệp và điểm vỡ nợ, được chuẩn hóa bằng cách chia cho độ lệch chuẩn của lợi suất tài sản.

DD= , 1"23(20)

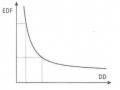
Xác suất vỡ nợ có mối quan hệ trước tiếp với khoảng cách tới điểm vỡ nợ. Nếu khoảng cách càng lớn thì xác suất càng nhỏ, doanh nghiệp ít có khả năng bị vỡ nợ.

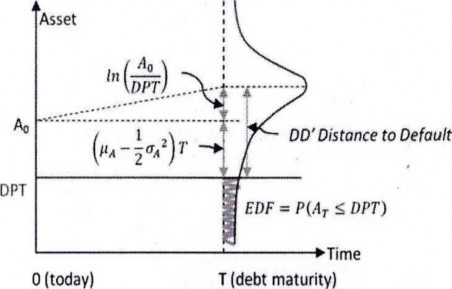
Hình 2.4. Khái niệm cơ bản mô hình KMV

Tính khoảng cách tới điểm vỡ nợ bao gồm hai bước:

1. Tính khoảng cách tới điểm vỡ nợ tuyết đối (Absolute Distance to Default- DD’)

2. Tính khoảng cách tới điểm vỡ nợ tương đối (Relative Distance to Default - DD)

Khoảng cách tới điểm vỡ nợ tuyết đối (DD’) được tính bằng khoảng cách giữa giá trị kỳ vọng của tài sản và điểm vỡ nợ (DPT) hay có thể hiểu là tổng của khoảng cách ban đầu và tăng trưởng của khoảng cách đó trong thời gian T

445= &' ( + + ( − 1+ 21

46 2

Khác với giả định trong mô hình Merton (1974), A trong mô hình KMV không phải là lãi suất phi rủi ro mà là lợi suất kì vọng của tài sản và sử dụng điểm vỡ nợ thay vì dùng mệnh giá trái phiếu K làm điểm quyết định vỡ nợ. Trong công thức (21) tăng

trưởng kỳ vọng bằng

− $2 chứ không bằng

do giả thuyết lợi suất theo

phân phối chuẩn nên lợi suất kì vọng sẽ theo phân phối chuẩn loga. Mối quan hệ giữa hai phân phối như sau:

&' 71~ # ( −, √+(22)

Chia khoảng cách tới điểm vỡ nợ tuyết đối cho độ lệch chuẩn của tài sản, ta có

được khoảng cách tới điểm vỡ nợ tương đối như sau:

Có thể thấy cách tính DD gần giống với cách tính d2 trong mô hình Merton trình