vượt quá VaR ước lượng, GARCH-EVT-copula-DVine-T có 5 quan sát mà mức tổn thất thực tế của danh mục vượt quá VaR ước lượng, phương pháp phân phối chuẩn có 8 quan sát mà mức tổn thất thực tế của danh mục vượt quá VaR ước lượng, phương pháp thực nghiệm có 5 quan sát mà mức tổn thất thực tế của danh mục vượt quá VaR ước lượng.
Bảng 3.6. Kết quả hậu kiểm các mô hình ước lượng VaR
Mô hình ước lượng VaR | Số vượt ngưỡng tối đa cho phép | Số thực tế vượt quá VaR | Độ sai lệch tuyệt đối trung bình | |
VaR(0.95) | GARCH-EVT-copula-T | 19 | 5 | 0.024125 |
GARCH-EVT-copula- Gauss | 19 | 6 | 0.023960 | |
GARCH-EVT-copula-DVine-T | 19 | 5 | 0.024758 | |
Phân phối chuẩn | 19 | 8 | 0.023990 | |
Thực nghiệm | 19 | 5 | 0.028579 | |
VaR(0.99) | GARCH-EVT-copula-T | 5 | 3 | 0.037410 |
GARCH-EVT-copula- Gauss | 5 | 3 | 0.037968 | |
GARCH-EVT-copula-DVine-T | 5 | 2 | 0.044472 | |
Phân phối chuẩn | 5 | 2 | 0.039653 | |
Thực nghiệm | 5 | 2 | 0.044569 |
Có thể bạn quan tâm!
-
So Sánh Kết Quả Ước Lượng Của Mô Hình Garch Và Ccc -
Đồ Thị Hàm Trung Bình Vượt Ngưỡng Mẫu Của Chuỗi Reib -
Phương Pháp Tham Số Với Giả Thiết Phân Phối Chuẩn -
Đề Xuất Các Hướng Nghiên Cứu Tiếp Theo -
Kết Quả Ước Lượng Các Mô Hình Hồi Quy Phân Vị -
Kết Quả Hồi Quy Hàm Đồng Vượt Ngưỡng Theo Bg Và Biến Trễ
Xem toàn bộ 209 trang tài liệu này.
Với mô hình VaR(0.99) tác giả thấy: Mô hình GARCH-EVT-copula-T có 3 quan sát mà mức tổn thất thực tế của danh mục vượt quá VaR ước lượng, mô hình GARCH-EVT-copula-Gauss có 3 quan sát mà mức tổn thất thực tế của danh mục vượt quá VaR ước lượng, GARCH-EVT-copula-DVine-T có 2 quan sát mà mức tổn thất thực tế của danh mục vượt quá VaR ước lượng, phương pháp phân phối chuẩn có 2 quan sát mà mức tổn thất thực tế của danh mục vượt quá VaR ước lượng, phương pháp thực nghiệm có 2 quan sát mà mức tổn thất thực tế của danh mục vượt quá VaR ước lượng.
Như vậy, số quan sát mà mức tổn thất thực tế của danh mục vượt quá VaR ước lượng của các mô hình đều nằm trong giới hạn cho phép của BIS ở cả 2 mức 95% và 99%.
Tuy nhiên, với mô hình VaR(0.95) thì độ sai lệch tuyệt đối trung bình khi ước lượng bởi mô hình GARCH-EVT-copula-Gauss bằng 0.023960 và là nhỏ nhất; với mô hình VaR(0.99) thì độ sai lệch tuyệt đối trung bình khi ước lượng bởi mô hình GARCH-EVT-copula-T bằng 0.037410 và là nhỏ nhất.
Như vậy, khi sử dụng phương pháp copula có điều kiện và EVT để ước lượng VaR của danh mục này thì kết quả thu được sẽ tốt hơn khi nhà đầu tư sử dụng giả định danh mục có phân phối chuẩn. Hơn nữa, ta có đồ thị hình ở 3.7 mô tả giá trị thực tế của danh mục và các giá trị ước lượng VaR(0.99) bằng các mô hình trên cho 250 quan sát :
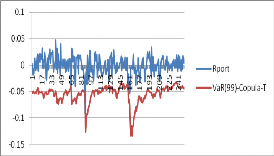
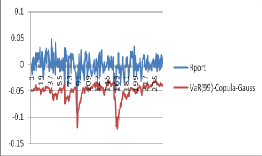
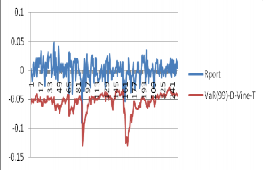
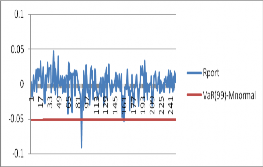
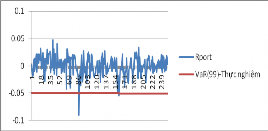
Hình 3.7. Hậu kiểm mô hình VaR(0.99)
Như vậy trong điều kiện thị trường hoạt động bình thường, VaR cho nhà đầu tư nắm giữ danh mục này biết trong một phiên giao dịch mức tổn thất (nếu có) tối đa là bao nhiêu với một độ tin cậy nào đó. Tuy nhiên khi những diễn biến bất thường của thị trường xảy ra, nếu muốn biết mức độ tổn thất của danh mục là bao nhiêu thì nhà đầu tư có thể dựa vào ES để dự đoán.
3.3.3. Ước lượng ES của danh mục đầu tư nhiều tài sản
Trong phần này, tác giả đi ước lượng ES(0.95) và ES(0.99) của danh mục lập từ 5 cổ phiếu: RCII, RFPT, RGMD, RKDC, RITA với trọng số bằng nhau bởi các mô hình: Mô hình GARCH-EVT-copula-T, mô hình GARCH-EVT-copula-Gauss, mô hình GARCH-EVT-copula-DVine-T, mô hình phân phối chuẩn, phân phối thực nghiệm. Đồng thời, tác giả cũng thực hiện hậu kiểm ES để so sánh tính phù hợp của các mô hình. Trước hết, ta có kết quả ước lượng ES của danh mục ở 2 mức 0.95 và
0.99 bằng 5 mô hình trên với 1241 quan sát đầu tiên:
Bảng 3.7. Ước lượng ES của 1241 quan sát đầu tiên ở 2 mức 0.95 và 0.99
GARCH- EVT- copula-T | GARCH- EVT-copula- Gauss | GARCH- EVT-copula -DVine-T | Phân phối chuẩn | Thực nghiệm | |
ES(0.95,1 ngày) | -0.04596905 | -0.0441147 | -0.04874 | -0.04621162 | -0.051126156 |
ES(0.99,1 ngày) | -0.07313909 | -0.0665023 | -0.07796 | -0.059709656 | -0.068190381 |
Theo kết quả ước lượng ES tác giả nhận xét: Sau mỗi phiêu giao dịch tại sàn HOSE đối với nhà đầu tư nắm giữ danh mục này:
Trong tình huống xấu nếu lợi suất của danh mục giảm sâu vượt các ngưỡng VaR(0.95), theo các mô hình: GARCH-EVT-copula-T, GARCH-EVT-copula- Gauss, GARCH-EVT-copula-DVine-T, phân phối chuẩn, phương pháp thực nghiệm thì 95% khả năng mức giảm dự tính tương ứng là 4.596905%, 4.41147%, 4.874%, 4.621162%, 5.1126156%.
Trong tình huống xấu nếu lợi suất của danh mục giảm sâu vượt các ngưỡng VaR(0.99), theo các mô hình: GARCH-EVT-copula-T, GARCH-EVT-copula- Gauss, GARCH-EVT-copula-DVine-T, phân phối chuẩn, phương pháp thực nghiệm thì 99% khả năng mức giảm dự tính tương ứng là 7.313909%, 6.65023%, 7.796%, 5.9709656%, 6.8190381%.
Tiếp theo, tác giả thực hiện hậu kiểm mô hình ES cho các phương pháp ước lượng ES đã xét ở trên. Tương tự như mô hình VaR, đối với mô hình ES tác giả cũng thực hiện hậu kiểm với 250 quan sát tiếp theo (từ quan sát 1242 đến quan sát 1491), nghĩa là chúng ta cho cửa sổ gồm 1241 quan sát di chuyển 250 lần, tại mỗi lần chúng ta lại ước lượng ES của danh mục cho các phương pháp trên.
Sau khi ước lượng được 250 giá trị ES của danh mục, tác giả tiến hành so sánh giá trị thu lỗ thực tế của danh mục và giá trị ES ước lượng để đánh giá sai số. Tác giả so sánh những mức tổn thất thực tế của danh mục đã vượt quá VaR ước lượng với ES ước lượng. Sau đó, tác giả tính sai số trung bình tuyết đối cho mỗi phương pháp. Ta có bảng kết quả hậu kiểm ES ở 2 mức tin cậy 0.95 và 0.99:
Bảng 3.8. Hậu kiểm ES ở 2 mức 0.95 và 0.99
GARCH- EVT- copula-T | GARCH- EVT- copula- Gauss | GARCH- EVT-copula -DVine-T | Phân phối chuẩn | Thực nghiệm | ||
MAS | ES(0.95,1 ngày) | 0.000301141 | 0.00034122 | 0.000309 | 0.00033282 | 0.000259675 |
ES(0.99,1 ngày) | 0.000110719 | 0.00011077 | 0.000085528 | 0.000149318 | 0.000157367 |
Theo kết quả hậu kiểm ES cho 250 ngày, tác giả nhận thấy:
Với ES(0.95): Giá trị sai số trung bình tuyệt đối (MAS) khi ước lượng bằng các mô hình: GARCH-EVT-copula-T, GARCH-EVT-copula-Gauss, GARCH-EVT-copula-DVine-T, phân phối chuẩn, phương pháp thực nghiệm tương ứng là: 0.000301141, 0.00034122, 0.000309, 0.00033282,
0.000259675. Có thể cho rằng các mô hình GARCH-EVT-copula-T, GARCH-EVT-copula-DVine-T, thực nghiệm có sai số trung bình tuyệt đối nhỏ hơn sai số trung bình tuyệt đối ước lượng bằng phân phối chuẩn.
Với ES(0.99): Giá trị sai số trung bình tuyệt đối (MAS) khi ước lượng bằng các mô hình: GARCH-EVT-copula-T, GARCH-EVT-copula-Gauss, GARCH-EVT-copula-DVine-T, phân phối chuẩn, phương pháp thực nghiệm tương ứng là: 0.000110719, 0.00011077, 0.000085528, 0.000149318, 0.000157367. Trong đó các mô hình: GARCH-EVT-copula-T, GARCH- EVT-copula-Gauss, GARCH-EVT-copula-DVine-T đều có sai số trung bình tuyệt đối nhỏ hơn sai số trung bình tuyệt đối khi ước lượng bằng phân phối chuẩn.
Như vậy, với cả 2 mức 0.95 và 0.99, trong số các mô hình ước lượng ES nêu trên thì các mô hình GARCH-EVT-copula-T và GARCH-EVT-copula-DVine-T đều cho thấy tốt hơn khi sử dụng phân phối chuẩn. Ta có đồ thị của chuỗi lợi suất thực tế (Rport) và các chuỗi ước lượng của ES(0.99) bằng 5 mô hình trên cho 250 quan sát ở hình 3.8.
Như vậy, mức tổn thất kỳ vọng (ES) của danh mục đầu tư là một độ đo rủi ro bổ sung cho VaR. Trong tình huống xấu, mức tổn thất của danh mục vượt quá VaR thì ES giúp cho nhà đầu tư dự tính được mức tổn thất này là bao nhiêu. Với những ưu điểm hơn VaR, độ đo rủi ro ES ngày càng khẳng định vai trò của nó trong quản trị rủi ro tài chính. Cho đến nay đã có nhiều phương pháp tính VaR và ES, nhiều phương pháp dựa trên giả thiết lợi suất các tài sản có phân phối chuẩn, tuy nhiên giả thiết này thường không thỏa mãn với các chuỗi số liệu theo thời gian trong tài chính. Để khắc phục hạn chế này, kết hợp với mô phỏng Monte Carlo, luận án sử dụng phương pháp copula điều kiện và EVT để tính VaR và ES của danh mục đầu tư. Qua kết quả thực nghiệm cho thấy, phương pháp copula điều kiện và EVT là phù hợp và có thể phản ánh được giá trị tổn thất thực tế chính xác hơn khi sử dụng giả thiết lợi suất các tài sản có phân phối chuẩn.
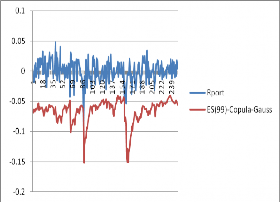
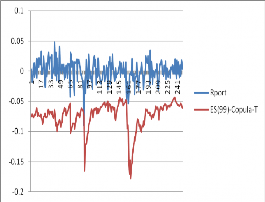
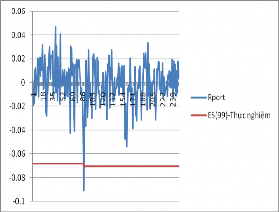
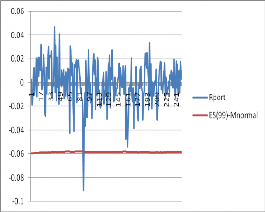
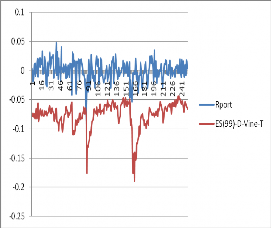
Hình 3.8. Hậu kiểm mô hình ES(0.99)
3.4. Kết luận chương 3
Chương này đã thực hiện phân tích thực nghiệm với một số mô hình đo lường rủi ro trên thị trường chứng khoán Việt Nam và đã thu được các kết quả như sau:
Ứng dụng mô hình GARCH để lựa chọn được mô hình phương sai sai số cho 21 chuỗi lợi suất: RBVH, RCTG, RDIG, RDPM, REIB, RHPG, RHSG, RIJC, RMBB, RMSN, ROGC, RPVF, RSBT, RVCB, RCII, RFPT, RGMD,
RKDC, RITA, RHNX, RVNINDEX có hiệu ứng ARCH. Kết quả ước lượng mô hình GARCH sẽ cho nhà đầu tư biết được tác động của những cú sốc trong quá khứ tác động nhiều hay ít tới độ biến động của lợi suất cổ phiếu đó ở thời điểm hiện tại. Dựa trên kết quả ước lượng mô hình GARCH, tác giả thấy rằng những cú sốc trong quá khứ làm cho rủi ro (phương sai có điều kiện) của một số cổ phiếu (DPM, IJC, VCB, FPT) tăng lên nhiều hơn so với những cổ phiếu khác trong khi đó lợi suất kỳ vọng của những cổ phiếu này lại nhỏ hơn; vì vậy nhà đầu tư nên cẩn trọng với những cổ phiếu này khi tham gia thị trường. Hơn nữa, chương này còn ứng dụng mô hình CCC để ước lượng đồng thời phương sai và hiệp phương sai có điều kiện cho một số cổ phiếu. Trên cơ sở kết quả ước lượng các mô hình GARCH, dựa theo hệ số beta trong mô hình CAPM, chương này cũng đã chỉ ra được sự biến động của rủi ro hệ thống của 11 cổ phiếu (những cổ phiếu có số quan sát là 1491): CII, FPT, GMD, KDC, ITA, DRC, PVD, REE, STB, VNM, VSH.
Dựa trên kết quả ước lượng VaR và ES bằng phương pháp EVT cho những chuỗi lợi suất không có phân phối chuẩn, ta có thể ước tính được mức tổn thất khi nắm giữ những cổ phiếu này. Tác giả có nhận xét: Dù trong hoàn cảnh xấu thì hiện tượng tất cả các cổ phiếu trên sàn HOSE, sàn HaSTC đồng loạt giảm giá kịch sàn hầu như không xảy ra. Hơn nữa, đối với các cổ phiếu: CII, FPT, GMD, KDC, PVD, STB, VSH, DRC, ITA, REE, VNM, VCB, SSI, PVF, VIC, SBT, PNJ, HSG, IJC, MBB, NTL, CTG, DIG, EIB, HAG, HPG
trong một phiên giao dịch với khả năng 95%, dù trong hoàn cảnh xấu thì việc mỗi cổ phiếu này giảm giá kịch sàn hầu như không xảy ra. Tuy nhiên trong hoàn cảnh xấu với khả năng 99%, các cổ phiếu: CII, FPT, KDC, PVD, STB, VSH, DRC, ITA, REE, VNM, VCB, SSI, VIC, SBT, PNJ, IJC, MBB, NTL,
CTG, DIG, EIB, HAG, HPG có thể giảm giá kịch sàn.
Ước lượng được VaR(0.95), VaR(0.99), ES(0.95), ES(0.99) của danh mục lập từ 5 cổ phiếu: RCII, RFPT, RGMD, RKDC, RITA với trọng số bằng nhau bởi các mô hình: Mô hình GARCH-EVT-copula-T, mô hình GARCH- EVT-copula-Gauss, mô hình GARCH-EVT-copula-DVine-T, mô hình phân phối chuẩn, phân phối thực nghiệm. Dựa trên kết quả hậu kiểm 250 quan sát của các mô hình trên, luận án chỉ ra phương pháp copula có điều kiện và EVT là phù hợp và có thể phản ánh được giá trị tổn thất thực tế chính xác hơn khi sử dụng giả thiết lợi suất các tài sản có phân phối chuẩn.